將要遠行,此時擱筆。
舊雨新知,後會有期。
─── 懸鉤子
俗話說︰千里搭長棚,沒有個不散的筵席。
2014 年 5 月 29 日始,日日為文至今幾近五年了。此刻停筆,當其時也。回顧昔時所寫文本系列︰
‧ 【鼎革‧革鼎】︰ RASPBIAN STRETCH 《六之 J.3‧MIR-1 》
‧ 光的世界︰引言
‧ W!O+ 的《小伶鼬工坊演義》︰神經網絡與深度學習【發凡】
……
祇怕早已江郎才盡,故宜有事遠行與讀者道別矣。
將要遠行,此時擱筆。
舊雨新知,後會有期。
─── 懸鉤子
俗話說︰千里搭長棚,沒有個不散的筵席。
2014 年 5 月 29 日始,日日為文至今幾近五年了。此刻停筆,當其時也。回顧昔時所寫文本系列︰
‧ 【鼎革‧革鼎】︰ RASPBIAN STRETCH 《六之 J.3‧MIR-1 》
‧ 光的世界︰引言
‧ W!O+ 的《小伶鼬工坊演義》︰神經網絡與深度學習【發凡】
……
祇怕早已江郎才盡,故宜有事遠行與讀者道別矣。
詩經‧國風‧豳風‧伐柯
伐柯如何?匪斧不克。
取妻如何?匪媒不得。
伐柯伐柯,其則不遠。
我覯之子,籩豆有踐。
伐『![]() 』柯即是製作斧柄,卻是非斧不行??將之比作娶『妻』
』柯即是製作斧柄,卻是非斧不行??將之比作娶『妻』
※《説文解字》: 柯,斧柄也。从木,可聲。
實在費疑猜??若思善用『工具』能夠創造更好的『工具』,那麼『伐柯伐柯,其則不遠。』果真『有理有則』的乎!?因此假借 SymPy 『符號矩陣』學習『矩陣』,也是『順理而行』的了?!
這裡僅以『基本矩陣』之法,求解一般 ![]() 矩陣之『反矩陣』
矩陣之『反矩陣』![]() 為例,演義這則『伐柯取妻』有趣之事︰
為例,演義這則『伐柯取妻』有趣之事︰
if
![]()
then
![]()
![]()
望可消消暑氣也!!??
─── 《光的世界︰派生科學計算四》
認識『初等矩陣』可得『高斯消去法』之精神,知道『陣列』的『元素乘法』易入『神經網路』世界︰
Michael Nielsen 先生此段文字是本章的重點,他先從
The backpropagation algorithm is based on common linear algebraic operations – things like vector addition, multiplying a vector by a matrix, and so on. But one of the operations is a little less commonly used. In particular, suppose s and t are two vectors of the same dimension. Then we use ![]() to denote the elementwise product of the two vectors. Thus the components of
to denote the elementwise product of the two vectors. Thus the components of ![]() are just
are just ![]() . As an example,
. As an example,
This kind of elementwise multiplication is sometimes called the Hadamard product or Schur product. We’ll refer to it as the Hadamard product. Good matrix libraries usually provide fast implementations of the Hadamard product, and that comes in handy when implementing backpropagation.
───
講起,是希望藉著『記號法』,方便讀者理解『反向傳播算法』的內容。這個稱作 Hadamard product 之『對應元素乘法』
In mathematics, the Hadamard product (also known as the Schur product[1] or the entrywise product[2]) is a binary operation that takes two matrices of the same dimensions, and produces another matrix where each element ij is the product of elements ij of the original two matrices. It should not be confused with the more common matrix product. It is attributed to, and named after, either French mathematician Jacques Hadamard, or German mathematician Issai Schur.
The Hadamard product is associative and distributive, and unlike the matrix product it is also commutative.
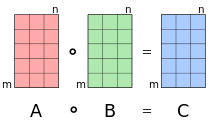
The Hadamard product operates on identically-shaped matrices and produces a third matrix of the same dimensions.
For two matrices, 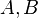 , of the same dimension,
, of the same dimension,  the Hadamard product,
the Hadamard product,  , is a matrix, of the same dimension as the operands, with elements given by
, is a matrix, of the same dimension as the operands, with elements given by
 .
.For matrices of different dimensions ( and
and  , where
, where  or
or  or both) the Hadamard product is undefined.
or both) the Hadamard product is undefined.
For example, the Hadamard product for a 3×3 matrix A with a 3×3 matrix B is:

───
明晰易解,大概無需畫蛇添足的吧!
─── 摘自《W!O+ 的《小伶鼬工坊演義》︰神經網絡【BACKPROPAGATION】四》
藉著『工具』改善『工具』︰
scipy.linalg)When SciPy is built using the optimized ATLAS LAPACK and BLAS libraries, it has very fast linear algebra capabilities. If you dig deep enough, all of the raw lapack and blas libraries are available for your use for even more speed. In this section, some easier-to-use interfaces to these routines are described.
All of these linear algebra routines expect an object that can be converted into a 2-dimensional array. The output of these routines is also a two-dimensional array.
scipy.linalg contains all the functions in numpy.linalg. plus some other more advanced ones not contained in numpy.linalg
Another advantage of using scipy.linalg over numpy.linalg is that it is always compiled with BLAS/LAPACK support, while for numpy this is optional. Therefore, the scipy version might be faster depending on how numpy was installed.
Therefore, unless you don’t want to add scipy as a dependency to your numpy program, use scipy.linalg instead of numpy.linalg
The classes that represent matrices, and basic operations such as matrix multiplications and transpose are a part of numpy. For convenience, we summarize the differences between numpy.matrix and numpy.ndarray here.
numpy.matrix is matrix class that has a more convenient interface than numpy.ndarray for matrix operations. This class supports for example MATLAB-like creation syntax via the semicolon, has matrix multiplication as default for the * operator, and contains I and T members that serve as shortcuts for inverse and transpose:
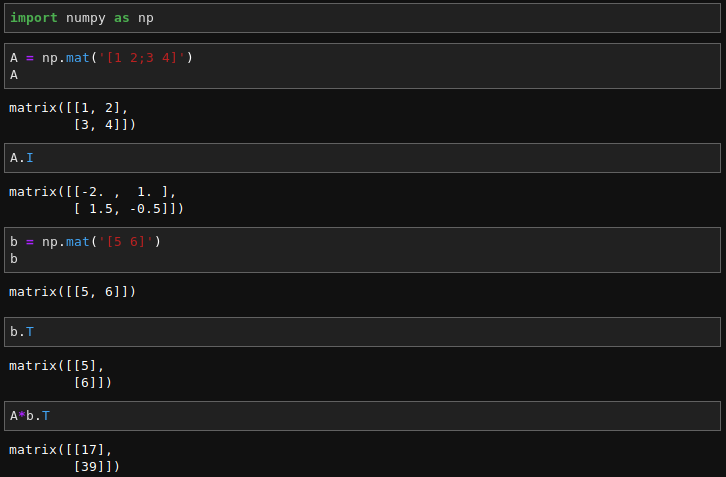
Despite its convenience, the use of the numpy.matrix class is discouraged, since it adds nothing that cannot be accomplished with 2D numpy.ndarray objects, and may lead to a confusion of which class is being used. For example, the above code can be rewritten as:
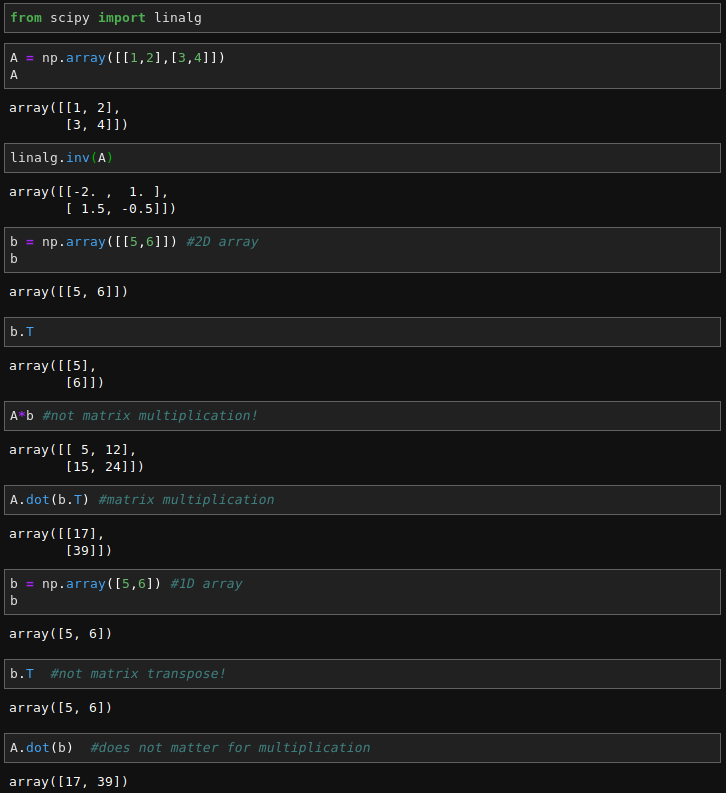
或離『伐柯其則』不遠,所以才串講也◎
在
《 Simply Logical
Intelligent Reasoning by Example 》
之第一部份起頭處, Peter Flach 開宗明義的講︰
Logic and Logic Programming
Logic Programming is the name of a programming paradigm which was developed in the 70s. Rather than viewing a computer program as a step-by-step description of an algorithm, the program is conceived as a logical theory, and a procedure call is viewed as a theorem of which the truth needs to be established. Thus, executing a program means searching for a proof. In traditional (imperative) programming languages, the program is a procedural specification of how a problem needs to be solved. In contrast, a logic program concentrates on a declarative specification of what the problem is. Readers familiar with imperative programming will find that Logic Programming requires quite a different way of thinking. Indeed, their knowledge of the imperative paradigm will be partly incompatible with the logic paradigm.
This is certainly true with regard to the concept of a program variable. In imperative languages, a variable is a name for a memory location which can store data of certain types. While the contents of the location may vary over time, the variable always points to the
same location. In fact, the term ‘variable’ is a bit of a misnomer here, since it refers to a value that is well-defined at every moment. In contrast, a variable in a logic program is a variable in the mathematical sense, i.e. a placeholder that can take on any value. In this respect, Logic Programming is therefore much closer to mathematical intuition than imperative programming.
Imperative programming and Logic Programming also differ with respect to the machine model they assume. A machine model is an abstraction of the computer on which programs are executed. The imperative paradigm assumes a dynamic, state-based machine model, where the state of the computer is given by the contents of its memory. The effect of a program statement is a transition from one state to another. Logic Programming does not assume such a dynamic machine model. Computer plus program represent a certain amount
of knowledge about the world, which is used to answer queries.
,指出『邏輯編程』和『 Von Neumann 程式語言』──
摘自《 CPU 機器語言的『解譯器』》︰
事實上 Von Neumann 的計算機架構,對於電腦程式語言的發展,有著極為深遠的影響,產生了現在叫做 Von Neumann 程式語言,與Von Neumann 的計算機架構,同形 isomorphism 同構︰
program variables ↔ computer storage cells
程式變數 對映 計算機的儲存單元
control statements ↔ computer test-and-jump instructions
控制陳述 對映 計算機的『測試.跳至』指令
assignment statements ↔ fetching, storing instructions
賦值陳述 對映 計算機的取得、儲存指令
expressions ↔ memory reference and arithmetic instructions.
表達式 對映 記憶體參照和算術指令
── 之『觀點』有極大的不同。通常這造成了學過一般程式語言的人『理解』上的困難。也可以說『邏輯編程』之『推導歸結』得到『證明』的想法遠離『圖靈機』的『狀態轉移』到達『接受』狀態 。反倒是比較接近『 λ運算』與『 Thue 字串改寫系統』抽象建構。讀者可以試著參考讀讀那些文章, 看看能否將『思考』方式的
Logic Programming requires quite a different way of thinking. Indeed, their knowledge of the imperative paradigm will be partly incompatible with the logic paradigm.
『不相容性』鎔鑄成整體思維之『結晶』,嫻熟用於解決各式各樣的『問題』!
也許『學習』到了一定的時候,或早或遲人們需要想想『學習方法 』,經由對自己的了解,找到『事半功倍』的有效作法。雖說人人都是獨特的,然而在『學習』上確實有很多類似的『難處』。比方說一般寫程式的思維,有所謂『從上往下』 Top-Down 以及『由底向頂』 Button-Up 思路取向不同。一者類似『歐式幾何』,從公理公設出發,逐步推演定理定律,邏輯清楚明白。然而一旦要自己去證明 □□ 定理時,有時總覺的無處下手。這是因為由『公理』通往『定理』的『推導歸結』之道路遙遠,常常看不出 ○□ 兩個『概念 』間竟然有如此的『聯繫』。另一彷彿『學會做菜』,由觀察親朋做菜開始,知道什麼菜要怎麼洗?怎麼切?用什麼方法調理?久而久之,學會了一道二道三道很多很多的菜的作法。也可以講,這樣的『學法』知道了許多『如何作』 Know-How ,很少思考『為什麼 』 Know-Why 這麼作,也很少形成一般『這一類』 Know-What 的菜,多半這樣作的『通則』。我們將要如何回答別人,自己『想都沒想過』,這菜『卻得這麼作』的『問題』?或許異地嫁娶之人,更能體會,這種『不同』就是『不同』的意思。
─── 《勇闖新世界︰ 《 PYDATALOG 》 導引《一》》
突如其來如,早年『邏輯編程』遭遇一事,闖入腦海震盪心胡!
忽爾思及『因式分解』問題??
『窮舉法』是一種通用方法。它以『問題』為『解』之『對錯』的『判準』,窮盡『所有可能』的『解』作『斷言』之求解法。或可同時參閱《 M♪o 之學習筆記本《寅》井井︰【䷝】試釋是事》文中所說之『蠻力法』以及例子︰
☿ ![]() 行︰雖說是蠻力法,實則乃用『窮舉』,數ㄕㄨˇ數ㄕㄨˋ數不盡,耗時難為功,怎曉
行︰雖說是蠻力法,實則乃用『窮舉』,數ㄕㄨˇ數ㄕㄨˋ數不盡,耗時難為功,怎曉 ![]() 機心迅捷後,此法遂真可行耶!?實習所用機,登入採『學號』與『針碼』【※ Pin Code 四位數字碼】。『學號』之制 ── 班碼-位碼 ──,班不過十,位少於百,故而極其數不足千。針碼有四位,總其量,只有萬。試而盡之,『千萬』已『窮舉』。問題當在『咸澤碼訊』有多快?『登錄』之法有 多嚴 ?破解程式幾人會?設使一應具足,那個『駭黑』之事,怕是恐難免!!……
機心迅捷後,此法遂真可行耶!?實習所用機,登入採『學號』與『針碼』【※ Pin Code 四位數字碼】。『學號』之制 ── 班碼-位碼 ──,班不過十,位少於百,故而極其數不足千。針碼有四位,總其量,只有萬。試而盡之,『千萬』已『窮舉』。問題當在『咸澤碼訊』有多快?『登錄』之法有 多嚴 ?破解程式幾人會?設使一應具足,那個『駭黑』之事,怕是恐難免!!……
此處特別指出計算機『速度提昇』使得『窮舉法』的實用性大增,對此法的了解也就更顯得重要了。
假使將『所有可能解』看成『解空間』,將『問題』當成『約束』條件,此時『問題』的『求解』,就轉換成『尋找』『解空間』中滿足『約束』條件的『解』。一般將之稱為『蠻力搜尋法』︰
In computer science, brute-force search or exhaustive search, also known as generate and test, is a very general problem-solving technique that consists of systematically enumerating all possible candidates for the solution and checking whether each candidate satisfies the problem’s statement.
A brute-force algorithm to find the divisors of a natural number n would enumerate all integers from 1 to the square root of n, and check whether each of them divides n without remainder. A brute-force approach for the eight queens puzzle would examine all possible arrangements of 8 pieces on the 64-square chessboard, and, for each arrangement, check whether each (queen) piece can attack any other.
While a brute-force search is simple to implement, and will always find a solution if it exists, its cost is proportional to the number of candidate solutions – which in many practical problems tends to grow very quickly as the size of the problem increases. Therefore, brute-force search is typically used when the problem size is limited, or when there are problem-specific heuristics that can be used to reduce the set of candidate solutions to a manageable size. The method is also used when the simplicity of implementation is more important than speed.
This is the case, for example, in critical applications where any errors in the algorithm would have very serious consequences; or when using a computer to prove a mathematical theorem. Brute-force search is also useful as a baseline method when benchmarking other algorithms or metaheuristics. Indeed, brute-force search can be viewed as the simplest metaheuristic. Brute force search should not be confused with backtracking, where large sets of solutions can be discarded without being explicitly enumerated (as in the textbook computer solution to the eight queens problem above). The brute-force method for finding an item in a table — namely, check all entries of the latter, sequentially — is called linear search.
上一篇因數的例子︰
── 摘自《勇闖新世界︰ 《 PYDATALOG 》【專題】之約束編程‧三》
故地重遊,想那時為何未論及『質數』哩!!
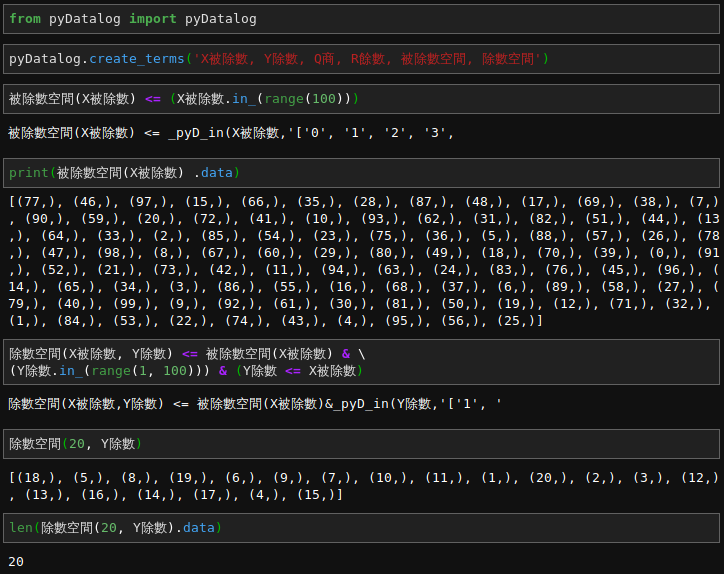
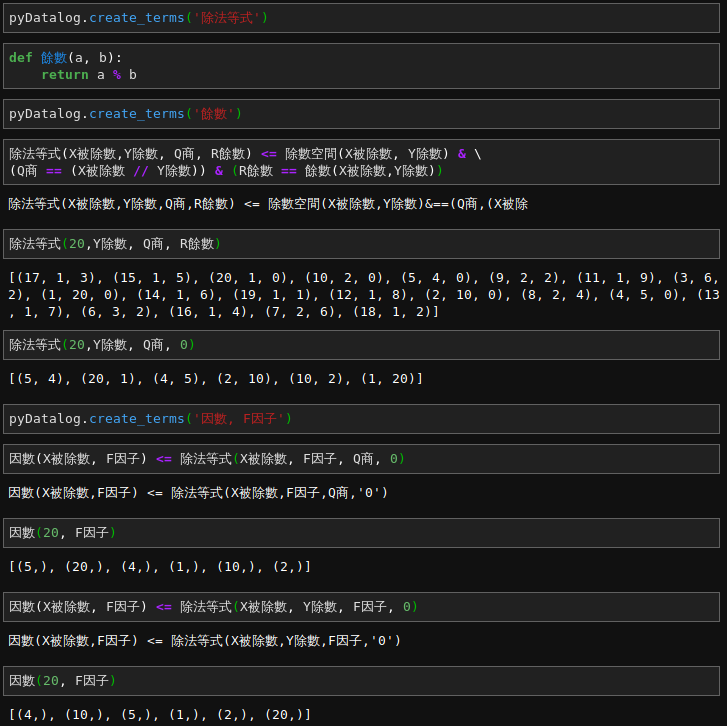
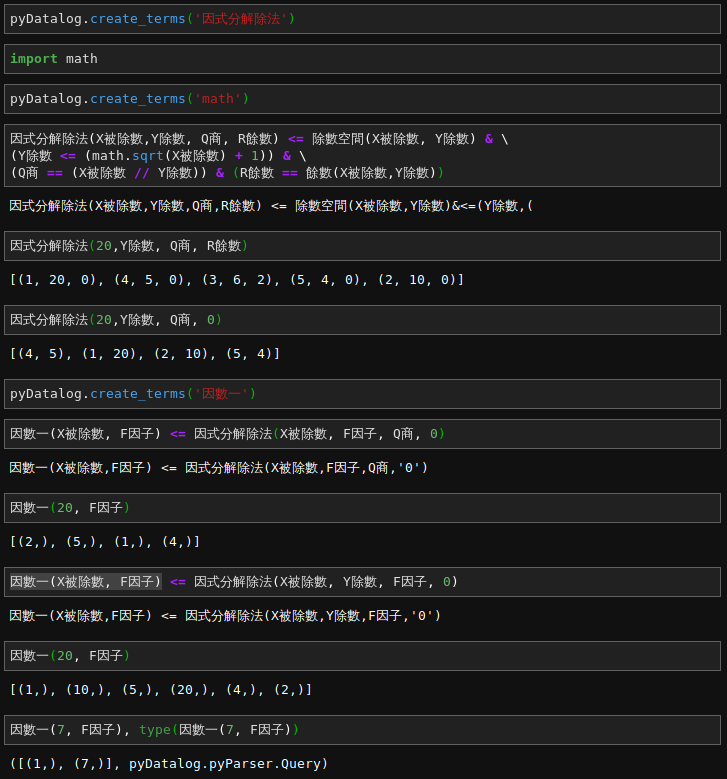
為 pyDatalog 語法以及資料型態所困乎?☻
或祇顧向前也!☺
由於此系列文本主旨在 NumPy 之陣列運算,雖特介紹 APL 語言,恐不宜喧賓奪主,因此有關該語言參考文件還請讀者自己研習哩︰
All our documentation is available free of charge in electronic form. In addition, Bernard Legrand’s Mastering Dyalog APL is available from Amazon.
Viewing PDF files requires Adobe Reader.
By default, Microsoft Windows blocks access to downloaded Compiled HTML Help (.chm) files. To enable access, right-click on each downloaded .chm file in Microsoft Windows explorer, select Properties from the drop-down menu and click Unblock.
Unless otherwise mentioned, the documentation on this page is for Dyalog version 17.0 and components shipped with that release. For other versions, see the links at the end of the page.
───
所以留心專注的是初始『設計』
Unlike traditionally structured programming languages, APL code is typically structured as chains of monadic or dyadic functions, and operators[50] acting on arrays.[51] APL has many nonstandard primitives (functions and operators) that are indicated by a single symbol or a combination of a few symbols. All primitives are defined to have the same precedence, and always associate to the right. Thus, APL is read or best understood from right-to-left.
Early APL implementations (circa 1970 or so) had no programming loop-flow control structures, such as do or while loops, and if-then-else constructs. Instead, they used array operations, and use of structured programming constructs was often not necessary, since an operation could be performed on a full array in one statement. For example, the iota function (ι) can replace for-loop iteration: ιN when applied to a scalar positive integer yields a one-dimensional array (vector), 1 2 3 … N. More recent implementations of APL generally include comprehensive control structures, so that data structure and program control flow can be clearly and cleanly separated.
之『思維方法』也。
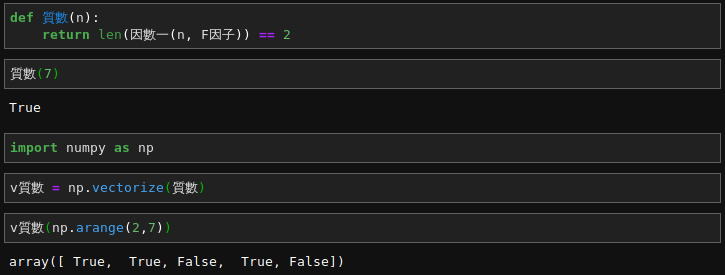
故假 APL 質數範例,擬借 NumPy 對應行之︰
※ 註︰
意在『經驗啟發』想法門徑耳☆
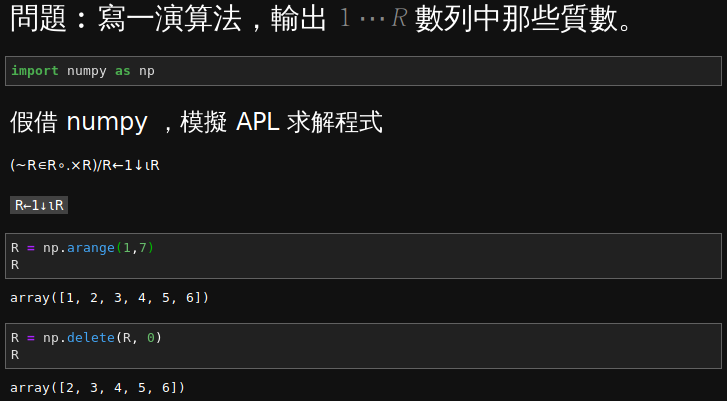
以 A 起頭的『高階』程式語言 APL 太過先進乎?所以一行就能得 ![]() 內之質數呦。
內之質數呦。
The following expression finds all prime numbers from 1 to R. In both time and space, the calculation complexity is ![]() (in Big O notation).
(in Big O notation).
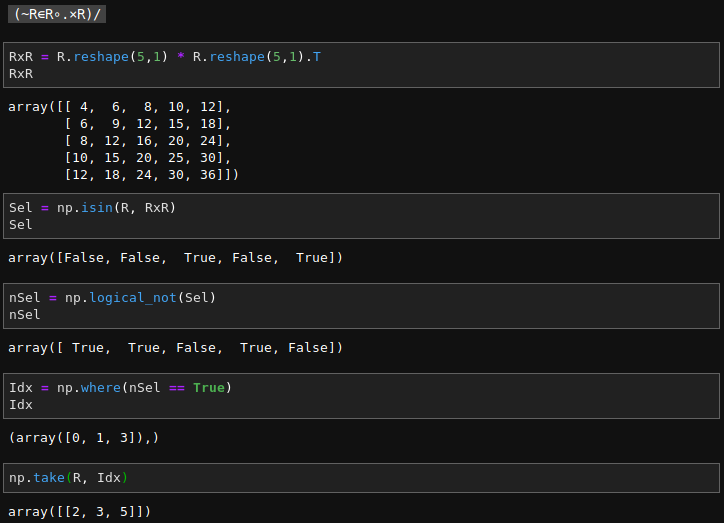
(~R∊R∘.×R)/R←1↓ιR
Executed from right to left, this means:
ι creates a vector containing integers from 1 to R (if R= 6 at the start of the program, ιR is 1 2 3 4 5 6)↓ function), i.e., 1. So 1↓ιR is 2 3 4 5 6R to the new vector (←, assignment primitive), i.e., 2 3 4 5 6/ reduction operator is dyadic (binary) and the interpreter first evaluates its left argument (fully in parentheses):R multiplied by R, i.e., a matrix that is the multiplication table of R by R (°.× operator), i.e.,| 4 | 6 | 8 | 10 | 12 |
| 6 | 9 | 12 | 15 | 18 |
| 8 | 12 | 16 | 20 | 24 |
| 10 | 15 | 20 | 25 | 30 |
| 12 | 18 | 24 | 30 | 36 |
R with 1 in each place where the corresponding number in R is in the outer product matrix (∈, set inclusion or element of or Epsilon operator), i.e., 0 0 1 0 1∼, logical not or Tilde operator), i.e., 1 1 0 1 0R for which the corresponding element is 1 (/ reduction operator), i.e., 2 3 5(Note, this assumes the APL origin is 1, i.e., indices start with 1. APL can be set to use 0 as the origin, so that ι6 is 0 1 2 3 4 5, which is convenient for some calculations.)
即使有人分解的說,概念貫串彷彿似『低階』組合語言,尚須細思慢嚼,要不易墬五里霧中裡。因此學習才需要天賦耶?
想那 ![]() 之自然數,可為質數或合成數。若
之自然數,可為質數或合成數。若 ![]() ,則
,則
![]() 也。
也。
故而一『否定』~ 再加上一『對應選擇』/足矣!
一時腦海迴盪著當年驚訝之事
沒有 if 以及 loop 語法結構,該如何寫程式ㄚ?
歡迎翱翔另類思考天空◎
APL (named after the book A Programming Language)[2] is a programming language developed in the 1960s by Kenneth E. Iverson. Its central datatype is the multidimensional array. It uses a large range of special graphic symbols[3] to represent most functions and operators, leading to very concise code. It has been an important influence on the development of concept modeling, spreadsheets, functional programming,[4] and computer math packages.[5] It has also inspired several other programming languages.[6][7]
…
APL has been both criticized and praised for its choice of a unique, non-standard character set. Some who learn it become ardent adherents, suggesting that there is some weight behind Iverson’s idea that the notation used does make a difference. In the 1960s and 1970s, few terminal devices and even display monitors could reproduce the APL character set. The most popular ones employed the IBM Selectric print mechanism used with a special APL type element. One of the early APL line terminals (line-mode operation only,not full screen) was the Texas Instruments TI Model 745 (circa 1977) with the full APL character set[42] which featured half and full duplex telecommunications modes, for interacting with an APL time-sharing service or remote mainframe to run a remote computer job,called an RJE.
Over time, with the universal use of high-quality graphic displays, printing devices and Unicode support, the APL character font problem has largely been eliminated. However, entering APL characters requires the use of input method editors, keyboard mappings, virtual/on-screen APL symbol sets,[43][44] or easy-reference printed keyboard cards which can frustrate beginners accustomed to other programming languages.[45][46][47] With beginners who have no prior experience with other programming languages, a study involving high school students found that typing and using APL characters did not hinder the students in any measurable way.[48]
In defense of APL use, APL requires less coding to type in, and keyboard mappings become memorized over time. Also, special APL keyboards are manufactured and in use today, as are freely available downloadable fonts for operating systems such as Microsoft Windows.[49] The reported productivity gains assume that one will spend enough time working in APL to make it worthwhile to memorize the symbols, their semantics, and keyboard mappings, not to mention a substantial number of idioms for common tasks.[citation needed]
Unlike traditionally structured programming languages, APL code is typically structured as chains of monadic or dyadic functions, and operators[50] acting on arrays.[51] APL has many nonstandard primitives (functions and operators) that are indicated by a single symbol or a combination of a few symbols. All primitives are defined to have the same precedence, and always associate to the right. Thus, APL is read or best understood from right-to-left.
Early APL implementations (circa 1970 or so) had no programming loop-flow control structures, such as do or while loops, and if-then-else constructs. Instead, they used array operations, and use of structured programming constructs was often not necessary, since an operation could be performed on a full array in one statement. For example, the iota function (ι) can replace for-loop iteration: ιN when applied to a scalar positive integer yields a one-dimensional array (vector), 1 2 3 … N. More recent implementations of APL generally include comprehensive control structures, so that data structure and program control flow can be clearly and cleanly separated.
The APL environment is called a workspace. In a workspace the user can define programs and data, i.e., the data values exist also outside the programs, and the user can also manipulate the data without having to define a program.[52] In the examples below, the APL interpreter first types six spaces before awaiting the user’s input. Its own output starts in column one.
……
A user may define custom functions which, like variables, are identified by name rather than by a non-textual symbol. The function header defines whether a custom function is niladic (no arguments), monadic (one right argument) or dyadic (left and right arguments), the local name of the result (to the left of the ← assign arrow), and whether it has any local variables (each separated by semicolon ‘;’).

Whether functions with the same identifier but different adicity are distinct is implementation-defined. If allowed, then a function CURVEAREA could be defined twice to replace both monadic CIRCLEAREA and dyadic SEGMENTAREA above, with the monadic or dyadic function being selected by the context in which it was referenced.
Custom dyadic functions may usually be applied to parameters with the same conventions as built-in functions, i.e., arrays should either have the same number of elements or one of them should have a single element which is extended. There are exceptions to this, for example a function to convert pre-decimal UK currency to dollars would expect to take a parameter with precisely three elements representing pounds, shillings and pence.[11]
Inside a program or a custom function, control may be conditionally transferred to a statement identified by a line number or explicit label; if the target is 0 (zero) this terminates the program or returns to a function’s caller. The most common form uses the APL compression function, as in the template (condition)/target which has the effect of evaluating the condition to 0 (false) or 1 (true) and then using that to mask the target (if the condition is false it is ignored, if true it is left alone so control is transferred).
Hence function SEGMENTAREA may be modified to abort (just below), returning zero if the parameters (DEGREES and RADIUS below) are of different sign:
∇ AREA←DEGREES SEGMENTAREA RADIUS ; FRACTION ; CA ; SIGN ⍝ local variables denoted by semicolon(;) FRACTION←DEGREES÷360 CA←CIRCLEAREA RADIUS ⍝ this APL code statement calls user function CIRCLEAREA, defined up above. SIGN←(×DEGREES)≠×RADIUS ⍝ << APL logic TEST/determine whether DEGREES and RADIUS do NOT (≠ used) have same SIGN 1-yes different(≠), 0-no(same sign) AREA←0 ⍝ default value of AREA set = zero →SIGN/0 ⍝ branching(here, exiting) occurs when SIGN=1 while SIGN=0 does NOT branch to 0. Branching to 0 exits function. AREA←FRACTION×CA ∇
The above function SEGMENTAREA works as expected if the parameters are scalars or single-element arrays, but not if they are multiple-element arrays since the condition ends up being based on a single element of the SIGN array – on the other hand, the user function could be modified to correctly handle vectorized arguments. Operation can sometimes be unpredictable since APL defines that computers with vector-processing capabilities should parallelise and may reorder array operations as far as possible – thus, test and debug user functions particularly if they will be used with vector or even matrix arguments. This affects not only explicit application of a custom function to arrays, but also its use anywhere that a dyadic function may reasonably be used such as in generation of a table of results:
90 180 270 ¯90 ∘.SEGMENTAREA 1 ¯2 4 0 0 0 0 0 0 0 0 0 0 0 0
A more concise way and sometimes better way – to formulate a function is to avoid explicit transfers of control, instead using expressions which evaluate correctly in all or the expected conditions. Sometimes it is correct to let a function fail when one or both input arguments are incorrect – precisely to let user know that one or both arguments used were incorrect. The following is more concise than the above SEGMENTAREA function. The below importantly correctly handles vectorized arguments:
∇ AREA←DEGREES SEGMENTAREA RADIUS ; FRACTION ; CA ; SIGN
FRACTION←DEGREES÷360
CA←CIRCLEAREA RADIUS
SIGN←(×DEGREES)≠×RADIUS
AREA←FRACTION×CA×~SIGN ⍝ this APL statement is more complex, as a one-liner - but it solves vectorized arguments: a tradeoff - complexity vs. branching
∇
90 180 270 ¯90 ∘.SEGMENTAREA 1 ¯2 4
0.785398163 0 12.5663706
1.57079633 0 25.1327412
2.35619449 0 37.6991118
0 ¯3.14159265 0
Avoiding explicit transfers of control also called branching, if not reviewed or carefully controlled – can promote use of excessively complex one liners, veritably “misunderstood and complex idioms” and a “write-only” style, which has done little to endear APL to influential commentators such as Edsger Dijkstra.[12] Conversely however APL idioms can be fun, educational and useful – if used with helpful comments ⍝, for example including source and intended meaning and function of the idiom(s). Here is an APL idioms list, an IBM APL2 idioms list here[13] and Finnish APL idiom library here.
………