求知者有所求乎?
《莊子‧秋水》上說了一則故事︰
莊子釣於濮水,楚王使大夫二人往先焉,曰:『願以境內累矣!』 莊子持竿不顧,曰:『吾聞楚有神龜,死已三千歲矣,王巾笥而藏之廟堂之上。此龜者,寧其死為留骨而貴乎,寧其生而曳尾於塗中乎?』二大夫曰:『寧生而曳尾塗中。』莊子曰:『往矣!吾將曳尾於塗中。』
,然後在《莊子‧養生主》中又講︰
吾生也有涯,而知也無涯。以有涯隨無涯,殆已;已而為知者,殆而已矣。為善無近名,為惡無近刑,緣督以為經,可以保身,可以全生,可以養親,可以盡年。
難道莊子是反對『學習』的嗎?也許相互對比著看,或許他祇想說生物的貪生怕死自然而然,然而人卻自以為貴又喜歡追名逐利,這根本不是為著知,僅是想知道更多『有用的』東西,他擔心如果人連『生命』都保不住了,那『學問』又有什麼用呢??
學問果真無境界耶??
任教於水木清華又是四大導師之一的王國維先生在他的大作《人間詞話》裡說到他『治學經驗』,是這麼講的
古今之成大事業、大學問者,必須經過三種之境界︰『昨夜西風凋碧樹,獨上高樓,望盡天涯路。』此第一境也。『衣帶漸寬終不悔,為伊消得人憔悴。』此第二境也。『眾裡尋他千百度,回頭暮見,那人正在,燈火欄珊處。』此第三境也。
作者並不能知道他為何『錯記』或是『記錯』了第三個境界?那裡寫的『眾裡尋他千百度,回頭暮見,那人正在,燈火欄珊處。』當是辛棄疾的《青玉案 ‧元夕》之『眾裡尋他千百度。驀然回首,那人卻在,燈火闌珊處。』。或許就像德國的大心理學家西格蒙德·佛洛伊德的『夢的解析』一書所說的︰要講『遺忘』一事到底是何事呢?此事總發生於過去卻又老是影響著當下和未來!!
就讓我們自己踏入那河中哪怕只是一次;
蝶戀花 北宋 晏殊
檻菊愁煙蘭泣露,
羅幕輕寒,
燕子雙飛去。
明月不諳離恨苦,
斜光到曉穿朱戶。
昨夜西風凋碧樹,
獨上高樓,
望盡天涯路。
欲寄彩箋兼尺素,
山長水闊知何處?
蝶戀花 北宋 柳永
佇倚危樓風細細,望極春愁,黯黯生天際。
草色煙光殘照裏,無言誰會憑闌意?
擬把疏狂圖一醉,對酒當歌,強樂還無味。
衣帶漸寬終不悔,為伊消得人憔悴。
青玉案‧元夕 南宋 辛棄疾
東風夜放花千樹,更吹落、星如雨。
寶馬雕車香滿路。鳳簫聲動,玉壺光轉,一夜魚龍舞。
蛾兒雪柳黃金縷,笑語盈盈暗香去。眾裡尋他千百度。
驀然回首,那人卻在,燈火闌珊處。
;去感受那大地迴旋之流水淙淙,…往通向…心靈的一扇門扉…
─── 摘自《後生可畏!?》
既已知
白努利數起源於等冪求和公式
Theorem
Let n and p be positive integers.
Then:
![]()
where Bn denotes the nth Bernoulli number.
─── 摘自《時間序列︰生成函數‧漸近展開︰白努利 □○《四》》
難到會不想知
等冪求和公式在
![]()
![]()
,呼喚白努利『多項式』快出來!
Bernoulli polynomials
In mathematics, the Bernoulli polynomials occur in the study of many special functions and in particular the Riemann zeta function and the Hurwitz zeta function. This is in large part because they are an Appell sequence, i.e. a Sheffer sequence for the ordinary derivative operator. Unlike orthogonal polynomials, the Bernoulli polynomials are remarkable in that the number of crossings of the x-axis in the unit interval does not go up as the degree of the polynomials goes up. In the limit of large degree, the Bernoulli polynomials, appropriately scaled, approach the sine and cosine functions.
This article also discusses the Bernoulli polynomials and the related Euler polynomials, and the Bernoulli and Euler numbers.
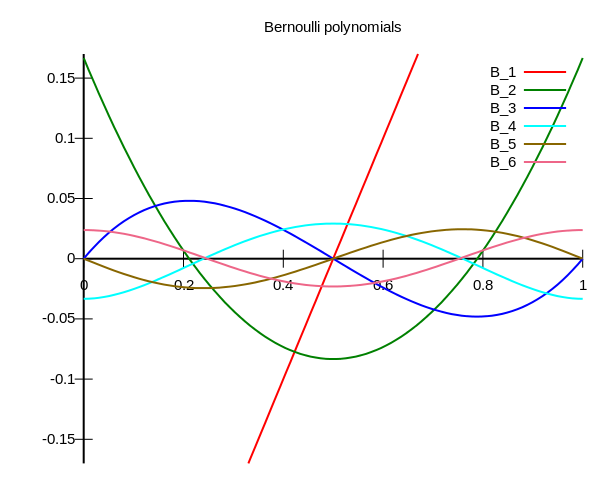
Bernoulli polynomials
Representations
The Bernoulli polynomials Bn admit a variety of different representations. Which among them should be taken to be the definition may depend on one’s purposes.
Explicit formula
for n ≥ 0, where bk are the Bernoulli numbers.
Generating functions
The generating function for the Bernoulli polynomials is
The generating function for the Euler polynomials is
Representation by a differential operator
The Bernoulli polynomials are also given by
where D = d/dx is differentiation with respect to x and the fraction is expanded as a formal power series. It follows that
cf. integrals below.
Representation by an integral operator
The Bernoulli polynomials are the unique polynomials determined by
on polynomials f, simply amounts to
This can be used to produce the inversion formulae below.
Explicit expressions for low degrees
The first few Bernoulli polynomials are:
─── 摘自《時間序列︰生成函數‧漸近展開︰白努利 □○《七》》
彼此關係嘛!總是他心通人理同的吧!!
就算不曉誰先用
![]() ,
,
其目的不可知嗎?
![]()
![]()
![]() 。
。
如是
![]()
![]()
![]()
![]()
![]() ,
,
若取 ![]() 、
、 ![]() 整數將之代換,加之得
整數將之代換,加之得
![]()
![]() 。
。
因此等冪求和公式可藉白努利多項式表示為
![]() 。
。