諺語說：人有失手，馬有亂蹄，這件事難保不會出紕漏。簡單的講︰吃燒餅哪有不掉芝麻的。是說不是『不可能』的，也就是『可能』的！那麼『百分之百』之『可能性』是否就意味『必然』的哩？科學家費米以擅長『合理估算』著名，他講『大象說』如雷貫耳，那麼當他提出

費米悖論

費米悖論（Fermi paradox，又稱費米謬論）闡述的是對地外文明存在性的過高估計和缺少相關證據之間的矛盾^[1]。宇宙驚人的年齡和龐大的星體數量意味著，除非地球是一個特殊的例子，否則地外生命應該廣泛存在^[2] 。在1950年的一次非正式討論中，物理學家恩里科·費米問道，如果銀河系存在大量先進的地外文明，那麼為什麼連飛船或者探測器之類的證據都看不到。對這個話題更加具體的探討最早出現在1975年麥克·哈特的文章中，有時也被叫做麥克·哈特悖論^[3]。另一個緊密相關的問題是大沉默——即使難以星際旅行，如果生命是普遍存在的話，為什麼我們探測不到電磁信號？有人嘗試通過尋找地外文明的證據來解決費米悖論，也提出這些生命可能不具備人類的智慧。也有學者認為高等地外文明根本不存在，或者非常稀少以至於人類不可能聯繫得上。地球殊異假說有時被認為為費米悖論提供了一種解釋的答案。

從哈特開始，很多人開始發展關於地外文明的科學理論或模型。大部分工作都引用費米悖論作為參考。很多相關的問題已經得到重視，內容包括天文學、生物學、生態學和哲學。新興的天體生物學給問題的解決引入了跨學科的研究手段。

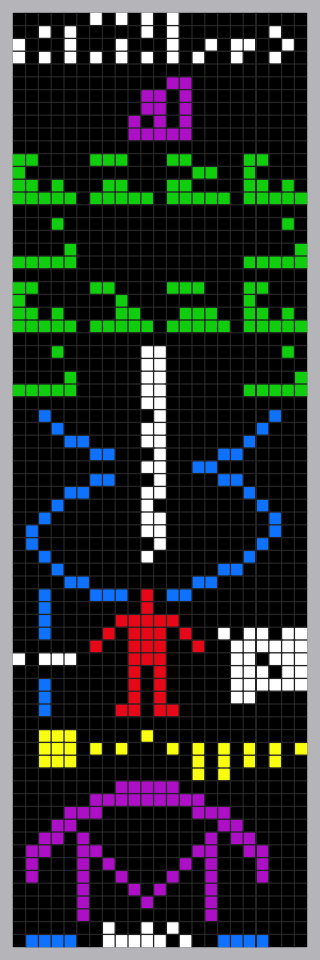
阿雷西博信息，顏色是用作分類，信息本身沒有任何顏色。人類首次嘗試利用電磁波尋找外星生命

時，豈可掉以輕心乎？尤其是它還關切人類在宇宙之地位耶？？

悖論基礎

費米悖論講述的是有關尺度和機率的論點和稀缺的證據之間的矛盾，其基本內涵表述如下：

宇宙顯著的尺度和年齡意味著高等地外文明應該存在。
The apparent size and age of the universe suggest that many technologically advanced extraterrestrial civilizations ought to exist.
但是，這個假設得不到充分的證據支持。
However, this hypothesis seems inconsistent with the lack of observational evidence to support it.

費米悖論的第一點，即尺度問題，是一個數量級估計：銀河系大約有2500億（2.5 x 10¹¹）顆恆星，可觀測宇宙內則有700垓（7 x 10²²）顆。即使智慧生命以很小的機率出現在圍繞這些恆星的行星中，那麼僅僅在銀河系內就應該有相當大數量的文明存在。這也符合平庸原理的觀點，即地球不是特殊的，僅僅是一個典型的行星，具有和其他星體相同的規律和現象。有人用德雷克公式來支持這個論點，儘管這個式子的基礎正在受到質疑。

費米悖論的第二點是對尺度觀點的答覆：考慮到智慧生命克服資源稀缺的能力和對外擴張的傾向性，任何高等文明都很可能會尋找新的資源和開拓他們所在的恆星系統，然後是涉足鄰近的星系。因為在宇宙誕生137億年之後，我們沒有在地球或可觀測宇宙的其他地方，找到其他智慧生命存在的切實可靠的證據；可以認為智慧生命是很稀少的，或者說我們對智慧生命的一般行為的理解是有誤的。

費米悖論可以表述成兩種形式。一種是「為什麼沒有發現外星人或者外星物品？」如果星際旅行是可行的話，即使是用人類造的飛船這樣緩慢地旅行，也只需要5百萬到5千萬年去征服星系。就算不考慮宇宙尺度，在地質學尺度上這也是一個相當短的時間。因為有很多年齡比太陽更大的恆星，或者因為智慧生命可能進化得更早，這個問題就變成為什麼星系還沒有被殖民。即使殖民對所有外星文明來說是不合實際的或者是不想去做的，大規模的星際探索也應該是有可能（探索的方式和理論上的探測器會在下文具體討論）。然而，沒有任何關於殖民和探索的證據得到承認。

上面的討論可能並沒有把宇宙作為整體考慮在內，因為星際旅行的次數問題就足以解釋為什麼地球上缺少外星生物的證據。但是，問題就變成「為什麼我們看不到智慧生命的跡象？」，因為足夠高等的文明應該能在可觀測宇宙的較大範圍內被看見。即使這些文明是很稀少的，尺度問題的討論暗示他們可能在宇宙歷史中的某一段存在過。因為他們在相當長的一段時間內能夠被觀測到，我們視野範圍內應該能找到很多他們起源地的跡象。然而，沒有任何確切的地外文明的觀測證據。

相同的，以尺度和機率的角度與視野來觀察，地球屬於適居帶的行星，擁有且滿足一切生物物種維持生命、生存和演化的所有條件，然而事實上從地球歷史中的顯生宙開始至今，在這長達五億多年的歲月間和數百萬的生物物種中，只有一個物種成功的演化成為高等智慧生命－「人類」，而非多種多元的高等智慧生物並存於地球上，這顯示了在「相同條件」下，「高等智慧生命」並非如此的輕易出現和存在。同地球殊異假說一般，這或許為費米悖論提供了其中一個答案。

故早已實至名歸矣！

名字起源

1950年，物理學家恩里科·費米在洛斯阿拉莫斯國家實驗室工作。他在一次去吃午飯的路上，和同事埃米爾·康佩斯基、愛德華·泰勒、赫伯特·約克有一段普通的交談^[4]。一開始，他們談論當時流行的UFO報導和阿蘭·鄧的漫畫^[5]。漫畫把市內垃圾箱的失蹤歸咎於外星人的掠奪。接著他們談到未來十年內，人類能夠觀測到超光速運動的物體的機率大小。泰勒認為是百萬分之一，但費米覺得接近於十分之一。然後話題又轉向其他方面，直到午餐時費米突然問道「Where are they？」，即「他們在哪裡？」（也有說法是「Where is everybody?」，即「其他人在哪裡」)^[6]。據其中一個在場人士回憶，費米當時用了幾個估計的數值做了一系列的快速計算。（費米很擅長於用基本原理和少量的數據做出數量估計，詳見費米問題）依靠估算，他當時的結論是地球應該在很早以前被外星人訪問過，而且被訪問的次數遠不止一次^[6]^[4]。

其後有人用『模態邏輯』

Modal logic

Modal logic is a type of formal logic primarily developed in the 1960s that extends classical propositional and predicate logic to include operators expressing modality. A modal—a word that expresses a modality—qualifies a statement. For example, the statement “John is happy” might be qualified by saying that John is usually happy, in which case the term “usually” is functioning as a modal. The traditional alethic modalities, or modalities of truth, include possibility (“Possibly, p“, “It is possible that p“), necessity (“Necessarily, p“, “It is necessary that p“), and impossibility (“Impossibly, p“, “It is impossible that p“).^[1] Other modalities that have been formalized in modal logic include temporal modalities, or modalities of time (notably, “It was the case that p“, “It has always been that p“, “It will be that p“, “It will always be that p“),^[2]^[3] deontic modalities (notably, “It is obligatory that p“, and “It is permissible that p“), epistemic modalities, or modalities of knowledge (“It is known that p“)^[4] and doxastic modalities, or modalities of belief (“It is believed that p“).^[5]

A formal modal logic represents modalities using modal operators. For example, “It might rain today” and “It is possible that rain will fall today” both contain the notion of possibility. In a modal logic this is represented as an operator, “Possibly”, attached to the sentence “It will rain today”.

The basic unary (1-place) modal operators are usually written “□” for “Necessarily” and “◇” for “Possibly”. In a classical modal logic, each can be expressed by the other with negation:

\Diamond P\leftrightarrow \lnot \Box \lnot P;

\Box P\leftrightarrow \lnot \Diamond \lnot P.

Thus it is possible that it will rain today if and only if it is not necessary that it will not rain today; and it is necessary that it will rain today if and only if it is not possible that it will not rain today. Alternative symbols used for the modal operators are “L” for “Necessarily” and “M” for “Possibly”.^[6]

解析『語義』，發現『機率』的『不可能』性其實不同於『必然』之『不可能』，是否解決了『問題』的呢？？？假使將桌上之一塊木片，以其桌邊為坐標系，然後去此木片裡的所有有理數點，請問這時它的面積如何計算哩！！！

勒貝格測度

數學上，勒貝格測度是賦予歐幾里得空間的子集一個長度、面積、或者體積的標準方法。它廣泛應用於實分析，特別是用於定義勒貝格積分。可以賦予一個體積的集合被稱為勒貝格可測；勒貝格可測集A的體積或者說測度記作λ(A)。一個值為∞的勒貝格測度是可能的，但是即使如此，在假設選擇公理成立時，Rⁿ的所有子集也不都是勒貝格可測的。不可測集的「奇特」行為導致了巴拿赫-塔斯基悖論這樣的命題，它是選擇公理的一個結果。

問題起源

人們知道，區間的長度可以定義為端點值之差。若干個不交區間的並的長度應當是它們的長度之和。於是人們希望將長度的概念推廣為比區間更複雜的集合。

我們想構造一個映射m，它能將實數集的子集E映射為非負實數mE 。稱這樣的映射（集函數）為集合E的測度。最理想的情況應該是m具有以下性質：

mE對於實數集的所有子集E都有定義。
對於一個區間I，mI應當等於其長度（端點數值之差）。
如果{E_n}是一列不相交的集合，並且m在其上有定義，那麼 $m(\cup E_n) = \sum mE_n$ 。
m具有平移不變性，即如果一個m有定義的集合E的每個元素都加一個相同的實數（定義為 $\{x + y | x \in E\}$ ，記作E+y），那麼m(E+y)=mE。

遺憾的是，這樣的映射（集函數）是不存在的。人們只能退而求其次，尋找滿足其中部分條件的映射。其中一個例子是若爾當測度，它只滿足有限可加性（第三條性質希望具有可數可加性）。勒貝格測度是滿足後三條性質的例子。

依舊祇是『語義』的『解釋』吧？△

零測集

主條目：零測集

Rⁿ的子集是零測集，如果對於每一個ε > 0，它都可以用可數個區間的乘積來覆蓋，其總體積最多為ε。所有可數集都是零測集。

如果Rⁿ的子集的豪斯多夫維數小於n，那麼它就是關於n維勒貝格測度的零測集。在這裡，豪斯多夫維數是相對於Rⁿ上的歐幾里得度量（或任何與其等價的利普希茨度量）。另一方面，一個集合可能拓撲維數小於n，但具有正的n維勒貝格測度。一個例子是史密斯-沃爾泰拉-康托爾集，它的拓撲維數為0，但1維勒貝格測度為正數。

為了證明某個給定的集合A是勒貝格可測的，我們通常嘗試尋找一個「較好」的集合B，與A只相差一個零測集，然後證明B可以用開集或閉集的可數交集和並集生成。

誰又可壟斷『意義』之『詮釋』啊！▼

所以許多事會發生『同義反復』之『現象』，或知或不知而已夫。科學終究建立於『觀察』與『實驗』也☆☆

因此聽聞︰

方法能傳精神難，善用方法不簡單。

天生精神自己有，博學廣思勤鍛鍊。

Kline 教授說︰

$s_{2n} = \sum \limits_{\nu=1}^{\infty} \frac{1}{{\nu}^{2 n}} = {(-1)}^{n-1} \frac{{(2 \pi)}^{2 n}}{2 (2n)!} B_{2 n}$

此處 $B_{2n}$ 為白努利數。

是歐拉最好的勝利。

─ 摘自《時間序列︰生成函數‧漸近展開︰白努利 □○《九下》》

且又及於︰

為什麼以 $d_{4k}$ 為中心立論呢？答案請參考上一篇。這裡只強調有值也。

$B_{4n} = - \frac{2(4n)!}{(2 \pi)^{4n}} \sum \limits_{\nu=1}^{\infty} \frac{1}{{\nu}^{4 n}}$ 。
※

$\sum \limits_{k=3}^{\infty} \frac{1}{k^{4n}} \le \sum \limits_{k=3}^{\infty} \int_{k-1}^{k} \frac{dt}{t^{4n}} = \int_{2}^{\infty} \frac{dt}{t^{4n}} = \frac{2}{4n - 1} \cdot \frac{1}{2^{4n}}$

$1 < \sum \limits_{k=1}^{\infty} \frac{1}{k^{4n}} \le 1 + \frac{1}{2^{4n}} + \frac{2}{4n-1} \cdot \frac{1}{2^{4n}} = 1 + \frac{4n+1}{4n-1} \frac{1}{2^{4n}}$

$\lim \limits_{n \to \infty} \sum \limits_{k=1}^{\infty} \frac{1}{k^{4n}} = 1$ 。

而且 $n \ge 1, 4n - 3 \ge 0, 2(4n-1) - (4n+1) = 4n-3 \ge 0$ ，所以

$1 < \sum \limits_{k=1}^{\infty} \frac{1}{k^{4n}} \le 1+ 2 \cdot \frac{1}{2^4} = 1 + \frac{1}{8}$ 。

─── 摘自《時間序列︰生成函數‧漸近展開︰白努利多項式之根《八》》

或將會『揣想』和『衡量』

$\frac{B_{2n+2}}{B_{2n}} = \frac {\frac{2 (2n+2)!}{{(2 \pi)}^{2n+2}}}{\frac{2 (2n)!}{{(2 \pi)}^{2n}}} = \frac{(2n+2)(2n+1)}{4 {\pi}^2}$ 焉？

認為

$B_n (x) = B_0 x^n + \binom{n}{1} B_1 x^{n-1} + \cdots + \binom{n}{n-1} B_{n-1} x^1 + B_n = 0, \ B_0 = 1$

$= x^n ( 1 + \binom{n}{1} \frac{B_1}{x} + \cdots + \binom{n}{n-1} \frac{B_{n-1}}{x^{n-1}}) + B_n = 0$

，當 $n$ 很大，而且 $x$ 足夠大 $\binom{n}1} \frac{B_1}{x} + \cdots + \binom{n}{n-1} \frac{B_{n-1}}{x^{n-1}} \approx 0$ 時，難道不是

$\approx x^n + B_n = 0$ 耶？ $\therefore x \approx \sqrt[n]{-B_n}$ 。

那麼當 $n = 2k+1, \ k \ge 1$ 是奇數， $B_n =0$ ，因此 $x=0$ 合理乎？若是 $- B_n <0$ ，彷彿 $n=4k+2$ 的情況， $x$ 將為虛數耶？？故而偏好 $n=4k$ 之形式嗎？☆

如果真如是，所謂『邏輯一致性』或『意義自恰性』將迫使

$\frac{B_{4k+1}}{x} = x^{4k} (1+ \binom{4k+1}{1} \frac{B_1}{x} + \cdots + \binom{4k+1}{4k-1} \frac{B_{4k-1}}{x^{4k-1}}) + \binom{4k+1}{4k} B_{4k} = 0$

不得不然矣！☆

故 $\therefore x \approx \sqrt[{4k}]{ -B_{4k}(4k+1)} \approx \sqrt[{4k}] {-B_{4k}}$ 哉◎◎

日	一	二	三	四	五	六
« 3 月				5 月 »
						1
2	3	4	5	6	7	8
9	10	11	12	13	14	15
16	17	18	19	20	21	22
23	24	25	26	27	28	29
30

FreeSandal

每日彙整: 2017-04-19

時間序列︰生成函數‧漸近展開︰當白努利遇上傅立葉《III》