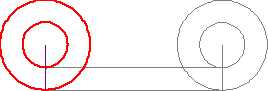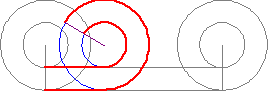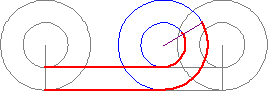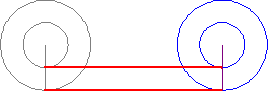
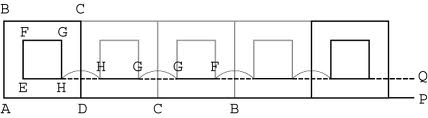
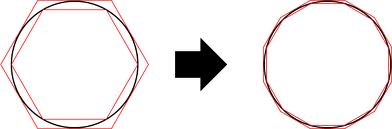
『此點』與『彼點』之『對應』難矣哉!不知『 □ 點』如何『重合 』『 ○ 點』耶?
公 元前三八四年亞里斯多德出生於色雷斯的斯塔基拉,他是哲學家柏拉圖的學生與亞歷山大大帝的老師。他一生著作豐富,囊括了物理學、形上學、詩歌、戲劇、音樂、 生物學、動物學、邏輯學、政治、政府、以及倫理學,乃西方哲學的奠基者之一。亞里斯多德的物理學思想 深刻的重塑了中世紀的學術思想 ,其影響力之大延伸到了 文藝復興時期,終被伽利略所改寫 ,後為牛頓物理學所取代。
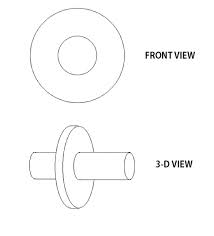
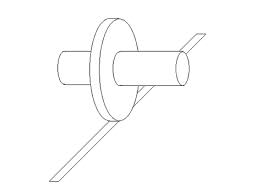
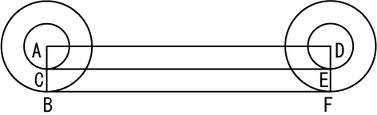
傳聞亞里斯多德著作了一本『 Mechanica or Mechanical Problems; Greek: Μηχανικά 』之力學書,這個『亞里斯多德之輪』 的悖論就是出自這本書 。滾動一個圓狀物,用它在平面上運動的『軌跡』就可以測量『圓周長』,這本是平凡無奇。但是左圖的動畫卻顯示, 大小二圓顯然走了一樣的『距離』,難道它們的『圓周長』一樣的嗎?由歐基里德的幾何學可以知道圓周長等於『 π ‧ 直徑』,這到底是怎麼回事呢?很清楚 ![]() ,難道不是這樣的嗎?一六三二年伽利略用義大利文撰寫了一部天文學著作,英文譯作『關於托勒密和哥白尼兩大世界體系的對話 』。在『第一天』的對話裡,他談到了『亞里斯多德之輪』︰
,難道不是這樣的嗎?一六三二年伽利略用義大利文撰寫了一部天文學著作,英文譯作『關於托勒密和哥白尼兩大世界體系的對話 』。在『第一天』的對話裡,他談到了『亞里斯多德之輪』︰
SALV. Otherwise what? Now since we have arrived at paradoxes let us see if we cannot prove that within a finite extent it is possible to discover an infinite number of vacua. At the same time we shall at least reach a solution of the most remarkable of all that list of problems which Aristotle himself calls wonderful; I refer to his Questions in Mechanics. This solution may be no less clear and conclusive than that which be himself gives and quite different also from that so cleverly expounded by the most learned Monsignor di Guevara.*
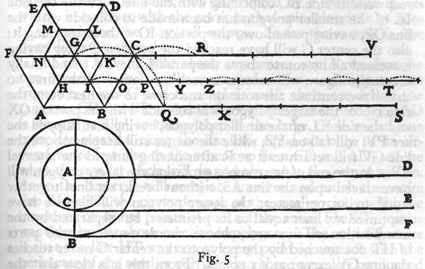
First it is necessary to consider a proposition, not treated by others, but upon which depends the solution of the problem and from which, if I mistake not, we shall derive other new and remarkable facts. For the sake of clearness let us draw an accurate figure. ……
為 了能更好的理解伽利略的觀點,就讓我們從今人對『無限』概念的說明開始。坎特爾依著萊布尼茲的思路,將數量『無限大』Infinity 定義成『比任何給定的實數還要大 』;以及將其『無限小』infinitesimal 定義成『比任何給定的實數還要小』。之後法國數學家柯西又用著『極限』limit 的概念來論述有著『無窮項』的『數列』或『級數』之『逼近值』,比方![]() 是指︰
是指︰
對於任何給定的 ![]() ,都找得到一個
,都找得到一個 ![]() ,
,
當 ![]() 時,
時, ![]() 。
。
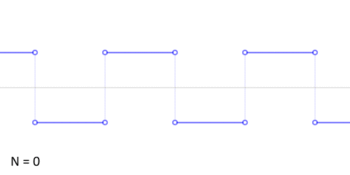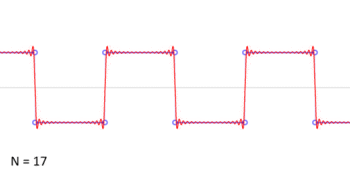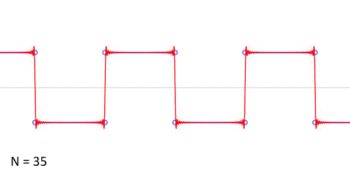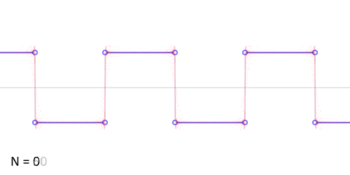
這固然是『嚴謹』的多了,但是對無限的『本性』是什麼並沒有說明?所以許多『誤謬』依然很容易發生?舉個例說,依上圖的方波想像這個無窮級數『 1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 …… 』,它是有極限值嗎?可以用下面各種不同的『計算法』嗎?
(1 – 1) + (1 – 1) + (1 – 1 )+ (1 – 1 )…… = 0 + 0 + 0 + 0 + …
1 + (-1 + 1 ) + (- 1 + 1 ) + (- 1 + 1) + ( – 1 …… = 1+0 + 0 + 0 + …
1 – 1 + 1 – 1 + 1 – 1 + 1 – 1 ……= (1+1+1+1+…) – (1+1+1+1+…)
在 『對話錄』裡伽利略說了一個自然數『平方的悖論』。 每一個自然數 ![]() 都可以平方成
都可以平方成 ![]() ,假使我們把自然數的集合稱作
,假使我們把自然數的集合稱作 ![]() ,將這個平方的集合叫做
,將這個平方的集合叫做 ![]() ,雖然它也有『無限多』的元素,顯然它的元素間的『差距』是越來越大的吧!這樣我們可以因為 N 有『更多的』的元素,就說
,雖然它也有『無限多』的元素,顯然它的元素間的『差距』是越來越大的吧!這樣我們可以因為 N 有『更多的』的元素,就說 ![]() 嗎?再說如果由
嗎?再說如果由 ![]() 構造另一個集合
構造另一個集合 ![]() ,這個集合中的每一個元素都從
,這個集合中的每一個元素都從 ![]() 中的元素『開方根』而來,那難到
中的元素『開方根』而來,那難到 ![]() 的元素個數不等於
的元素個數不等於 ![]() 的元素個數嗎?更不要說
的元素個數嗎?更不要說 ![]() 就是
就是 ![]() 吧!!他又用著『一對一』對應的相同之思路 ,論證一條『短的線段』和一條『長的線段』都是一樣『無窮的可分』,擁有『一樣多』的『點』。所以伽利略認為 『無限』並不是具有『數量』的『可比較』之性質,而『點』── 並非無窮可分的小 ── 卻是『不可分』的『非量』,此兩者都遠遠超越人類的『理解』。也許可以說他非常明白,一般數學的運算並不適用於這兩個『理念』,知道『向大』而無外之無限與 『往小』又無窮之可分,是兩種完全不一樣的『
吧!!他又用著『一對一』對應的相同之思路 ,論證一條『短的線段』和一條『長的線段』都是一樣『無窮的可分』,擁有『一樣多』的『點』。所以伽利略認為 『無限』並不是具有『數量』的『可比較』之性質,而『點』── 並非無窮可分的小 ── 卻是『不可分』的『非量』,此兩者都遠遠超越人類的『理解』。也許可以說他非常明白,一般數學的運算並不適用於這兩個『理念』,知道『向大』而無外之無限與 『往小』又無窮之可分,是兩種完全不一樣的『 ![]() 』。
』。
─── 摘自《亞里斯多德之輪!!》
難到『 □ 線』無有無窮『點』,卻而『偏逢』『 ○ 線 』不依然!『一點對一點』之『曲、直』滿射可以論『拓樸』;『透視眼見』終講『內涵規矩』◎
過去有人曾經想像過一種情況︰如果說宇宙中的一切,在夜間會突然的『變大』或者『縮小』,那麼我們能夠『發現』的嗎?假使從『量測』的觀點來看,如果度量用的『尺』 ![]() 隨著時間改變,『被度量事物』的『大小』
隨著時間改變,『被度量事物』的『大小』 ![]() 也『協同』的跟隨著變化
也『協同』的跟隨著變化 ![]() ,這樣在那個『宇宙』 裡面
,這樣在那個『宇宙』 裡面 ![]() ,也就是講『測量』沒有辦法『知道』到底『有沒有』發生過這件事的啊!!然而這卻更進一步引發了『自然定律』到底是否會在『度量單位』的改變下,而有所不同的呢??
,也就是講『測量』沒有辦法『知道』到底『有沒有』發生過這件事的啊!!然而這卻更進一步引發了『自然定律』到底是否會在『度量單位』的改變下,而有所不同的呢??
之前在《亞里斯多德之輪!!》一文中,我們談到了『伽利略』的『無窮觀』。一六三八年,伽利略在『兩種新科學』 Two New Sciences 一書中,提出了『平方立方定律』。假使一個『物體』等比例放大 ![]() 倍,那麼它的『面積』將放大
倍,那麼它的『面積』將放大 ![]() 倍,而且它的『體積』將放大
倍,而且它的『體積』將放大 ![]() 倍。這難到又有什麼奇怪的嗎?
倍。這難到又有什麼奇怪的嗎?
如果思考在大地上『重力』作用下『生物』之『承受力』的問題,當可以明白『壓力』是『單位面積』所負載的『重量』。如此將之『等比例放大』後,這個『壓力』 ![]() ,將正比於『放大倍率』
,將正比於『放大倍率』 ![]() ,所以說一棵樹,並不能夠一直向上生長,一隻螞蟻也很難變大數萬倍而不受影響的啊!如此講來天文學上所說的『宇宙膨漲』應該是有『現象』依據的吧!然而既然已經說是『宇宙』的了,它又該往『哪裡膨漲』的呢??或許《科赫傳說!!》裡的『雪花維度』是一個『起始點』的吧!!
,所以說一棵樹,並不能夠一直向上生長,一隻螞蟻也很難變大數萬倍而不受影響的啊!如此講來天文學上所說的『宇宙膨漲』應該是有『現象』依據的吧!然而既然已經說是『宇宙』的了,它又該往『哪裡膨漲』的呢??或許《科赫傳說!!》裡的『雪花維度』是一個『起始點』的吧!!
── 摘自《【Sonic π】電路學之補充《四》無窮小算術‧中下中‧中》
縱不知有無『自然單位長』之存在,亦當曉『度量』啟『數值化』的始點◎
且讓我們借著『透視性』之『抽象』定義︰
Projective geometry
In projective geometry the points of a line are called a projective range, and the set of lines in a plane on a point is called a pencil.
Given two lines and
in a plane and a point P of that plane on neither line, the bijective mapping between the points of the range of
and the range of
determined by the lines of the pencil on P is called a perspectivity (or more precisely, a central perspectivity with center P).[4] A special symbol has been used to show that points X and Y are related by a perspectivity;
In this notation, to show that the center of perspectivity is P, write
Using the language of functions, a central perspectivity with center P is a function
(where the square brackets indicate the projective range of the line) defined by
.[5] This map is an involution, that is,
.
The existence of a perspectivity means that corresponding points are in perspective. The dual concept, axial perspectivity, is the correspondence between the lines of two pencils determined by a projective range.
,嘗試『賦值』吧。
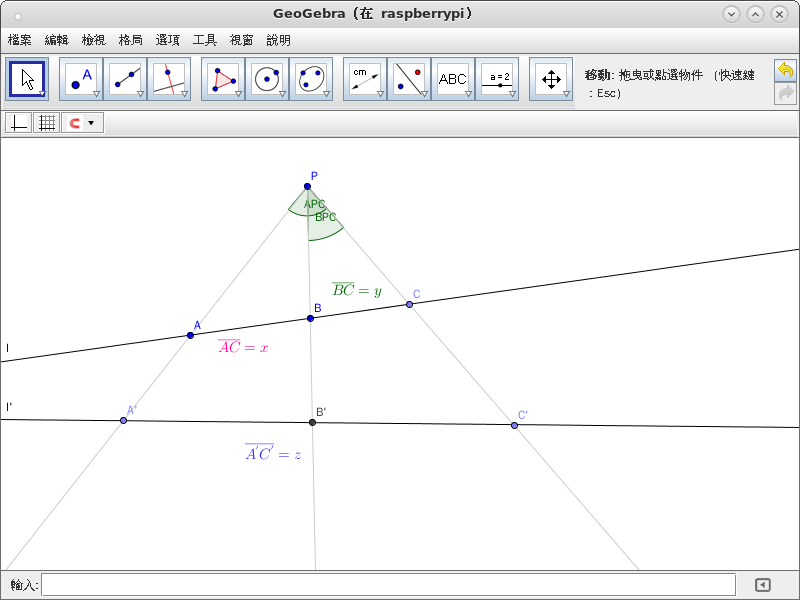
所謂某一『透視』,在給出『兩相異線』 ![]() 以及不在這兩線上的『一點』
以及不在這兩線上的『一點』 ![]() 就已確定。因為不論
就已確定。因為不論 ![]() 線上,任一點
線上,任一點 ![]() 所形成之
所形成之 ![]() 線,將交
線,將交 ![]() 線於唯一一點 ── 且稱
線於唯一一點 ── 且稱 ![]() ── 也。反之依然
── 也。反之依然 ![]() 線上任一點
線上任一點 ![]() 所形成之
所形成之 ![]() 線,亦將交
線,亦將交 ![]() 線於唯一一點
線於唯一一點 ![]() 也。
也。
由於相異兩點決定一條線,
![]()
依理明定了 ![]() 與
與 ![]() 『所有點』之間的『對射關係』。
『所有點』之間的『對射關係』。
如自『幾何推理』知道,若取 ![]() 為『定點』,則
為『定點』,則
![]() 。
。
自然 ![]() 也為『定點』,且
也為『定點』,且
![]() 矣。
矣。
因此『賦值』後之『數值關係』當滿足
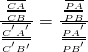 吧!
吧!
然而 ![]() 至少可有兩種選項
至少可有兩種選項
‧ ![]()
‧ ![]()
該如何選擇呢?★☆