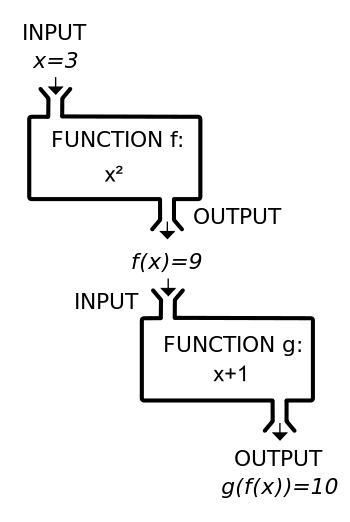
承上篇細咀嚼『透視』是什麼??所謂『線』之『名』 ![]() 虛字也!!
虛字也!!
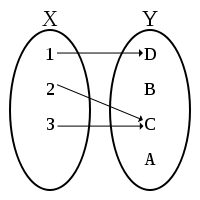
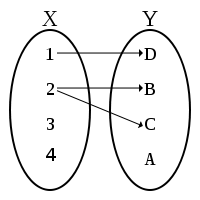
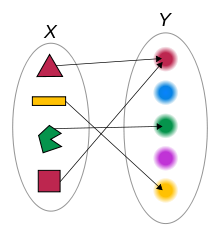
如果仔細考察 ![]() ── 比方說
── 比方說 ![]() ──,那麼『函數
──,那麼『函數 ![]() 』是什麼呢?『變數
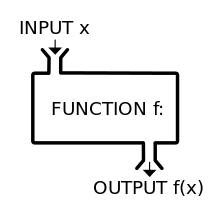
』是什麼呢?『變數 ![]() 』又是什麼呢?如果從函數定義可以知道『變數』並不是什麼『會變的數』,而是規定在『定義域』或者『對應域』中的『某數』的概念,也就是講在該定義的『集合元素中』談到『每一個』、『有一個』和『恰有一個』…的那樣之『指稱』觀念。這能有什麼困難的嗎?假使設想另一個函數
』又是什麼呢?如果從函數定義可以知道『變數』並不是什麼『會變的數』,而是規定在『定義域』或者『對應域』中的『某數』的概念,也就是講在該定義的『集合元素中』談到『每一個』、『有一個』和『恰有一個』…的那樣之『指稱』觀念。這能有什麼困難的嗎?假使設想另一個函數 ![]() ,它的定義域與對應域都和函數
,它的定義域與對應域都和函數 ![]() 一樣,那麼這兩個函數是一樣還是不一樣的呢?如果說它們是相同的函數,那麼這個所說的『函數』就該是『
一樣,那麼這兩個函數是一樣還是不一樣的呢?如果說它們是相同的函數,那麼這個所說的『函數』就該是『![]() 』,其中
』,其中 ![]() 『變數』只是『命名的』── 函數的輸出之數 ──,而且
『變數』只是『命名的』── 函數的輸出之數 ──,而且 ![]() 『變數』是『虛名的』── 函數的輸入之數 ──。如果從函數
『變數』是『虛名的』── 函數的輸入之數 ──。如果從函數 ![]() 將『輸入的數』轉換成『輸出的數』的觀點來看,這個『輸入與輸出』本就是
將『輸入的數』轉換成『輸出的數』的觀點來看,這個『輸入與輸出』本就是 ![]() 所『固有的』,所以和『輸入與輸出』到底是怎麼『命名』無關的啊!更何況『定義域或對應域』任一也都不必是『數的集合』,這時所講的『函數』或許稱作『函式』比較好,『變數』或該叫做『變元』。其次假使將多個函數『合成』composition,好比『輸出入』的串接,舉例來講,一般數學上表達成
所『固有的』,所以和『輸入與輸出』到底是怎麼『命名』無關的啊!更何況『定義域或對應域』任一也都不必是『數的集合』,這時所講的『函數』或許稱作『函式』比較好,『變數』或該叫做『變元』。其次假使將多個函數『合成』composition,好比『輸出入』的串接,舉例來講,一般數學上表達成 ![]() ,此時假使不補足,
,此時假使不補足,![]() 和
和 ![]() ,怕是不能知道這個函數的『結構』是什麼的吧?進一步講『函數』難道不能看成『計算操作子』operator 的概念,定義著什麼是
,怕是不能知道這個函數的『結構』是什麼的吧?進一步講『函數』難道不能看成『計算操作子』operator 的概念,定義著什麼是![]() 、
、![]() 、
、![]() 或
或 ![]() 的嗎?就像將之這樣定義成︰
的嗎?就像將之這樣定義成︰
![]()
,而將函數合成這麼定義為︰
![]()
。如此將使『函數』或者『二元運算』的定義域或對應域可以含括『函數』的物項,所以說它是『泛函式』functional 的了。
再者將函式的定義域由一數一物推廣到『有序元組』turple 也是很自然的事,就像講房間裡的『溫度函數』是 ![]() 一樣,然而這也產生了另一種表達的問題。假想
一樣,然而這也產生了另一種表達的問題。假想 ![]() 、
、 ![]() 和
和 ![]() ,這
,這 ![]() 兩個函數都是
兩個函數都是 ![]() 函數的『部份』partial 函數,構成了兩個不同的『函數族』。於是在一個運算過程中,這個表達式『
函數的『部份』partial 函數,構成了兩個不同的『函數族』。於是在一個運算過程中,這個表達式『 ![]() 』究竟是指什麼?是指『
』究竟是指什麼?是指『![]() 』還是指『
』還是指『![]() 』呢?也許說不定是指『
』呢?也許說不定是指『![]() 』的呢?難道說『兩平方數之差』本身就沒有意義的嗎??因是之故,邱奇所發展的『λ 記號法』是想要『清晰明白』的『表述』一個『表達式』所說之內容到底是指的什麼。如果使用這個記號法,
』的呢?難道說『兩平方數之差』本身就沒有意義的嗎??因是之故,邱奇所發展的『λ 記號法』是想要『清晰明白』的『表述』一個『表達式』所說之內容到底是指的什麼。如果使用這個記號法,![]() 記作︰
記作︰
![]()
![]()
![]()
。那麼之前的 ![]() 也可以寫成了︰
也可以寫成了︰
![]() 。
。
── 說是清晰明白的事理,表達起來卻未必是清楚易懂 ──
─── 摘自《λ 運算︰淵源介紹》
彼此交換又何妨呢??
且讓我們借著『透視性』之『抽象』定義︰
Projective geometry
In projective geometry the points of a line are called a projective range, and the set of lines in a plane on a point is called a pencil.
Given two lines and
in a plane and a point P of that plane on neither line, the bijective mapping between the points of the range of
and the range of
determined by the lines of the pencil on P is called a perspectivity (or more precisely, a central perspectivity with center P).[4] A special symbol has been used to show that points X and Y are related by a perspectivity;
In this notation, to show that the center of perspectivity is P, write
Using the language of functions, a central perspectivity with center P is a function
(where the square brackets indicate the projective range of the line) defined by
.[5] This map is an involution, that is,
.
The existence of a perspectivity means that corresponding points are in perspective. The dual concept, axial perspectivity, is the correspondence between the lines of two pencils determined by a projective range.
,嘗試『賦值』吧。
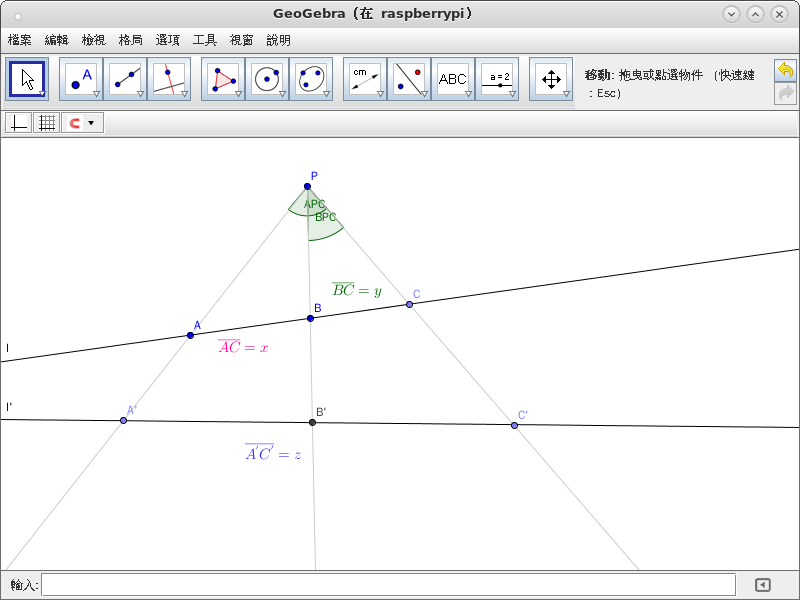
所 謂某一『透視』,在給出『兩相異線』 ![]() 以及不在這兩線上的『一點』
以及不在這兩線上的『一點』 ![]() 就已確定。因為不論
就已確定。因為不論 ![]() 線上,任一點
線上,任一點 ![]() 所形成之
所形成之 ![]() 線,將交
線,將交 ![]() 線於唯一一點 ── 且稱
線於唯一一點 ── 且稱 ![]() ── 也。反之依然
── 也。反之依然 ![]() 線上任一點
線上任一點 ![]() 所形成之
所形成之 ![]() 線,亦將交
線,亦將交 ![]() 線於唯一一點
線於唯一一點 ![]() 也。
也。
由於相異兩點決定一條線,
![]()
依理明定了 ![]() 與
與 ![]() 『所有點』之間的『對射關係』。
『所有點』之間的『對射關係』。
已從『幾何推理』知道,若取 ![]() 為『定點』,則
為『定點』,則
![]() 。
。
自然 ![]() 也為『定點』,且
也為『定點』,且
![]() 矣。
矣。
因此『賦值』後之『數值關係』當滿足
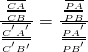 吧!
吧!
然而 ![]() 至少可有兩種選項
至少可有兩種選項
‧ ![]()
‧ ![]()
該如何選擇呢?★☆
然相異之線無窮,觀者亦無限也,
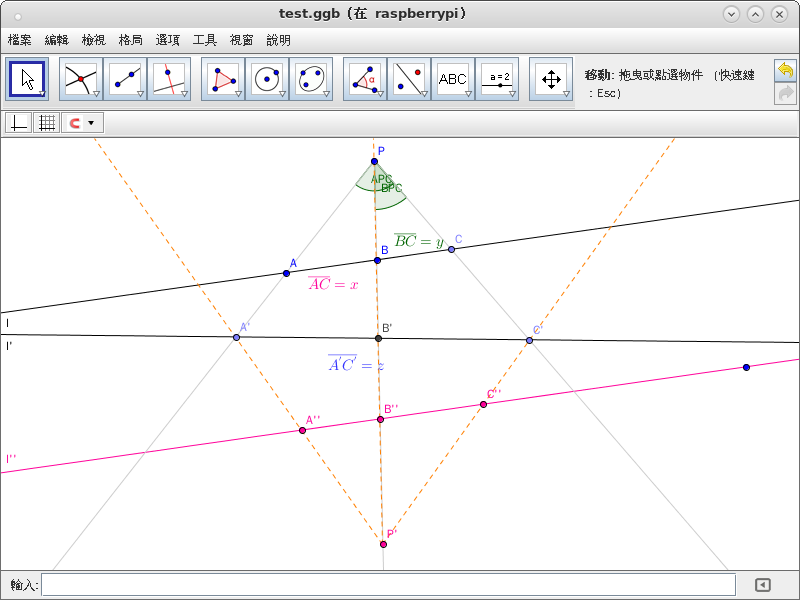
如何能夠『像之像』 ![]() 不變耶??
不變耶??
此所以說,因
![]() ,故優於選
,故優於選
![]()
的嘛!
莫非祇為存其義乎?
大哲學家亞里士多德認為自然界有一種『原因』Cause 關係,它用著『因為 Because 』回答了『為什麼』Why 之問題。他列舉了四種原因,故簡稱之為『四因說』︰
任何『事物』是由它所構成的『原料』、『組件』和『元素』,按著一套完整的『架構』、『組裝』與『結合』方式才形成的,這個『材質』的部份,就是『物質因』Material Cause ;而那個架構規劃的『藍圖』就是『形式因』Formal Cause,形式因也定義了『□之所以是□』。其次任何『事物』之『存在』總是有理由的,它因著『目的因』Final Cause 而能在時空中『存有』,又可能將隨著時流因之而被改變,這就推動著『動力因』Efficient Cause 去『改變什麼』?又會『如何將之改變』!!
那麼亞里士多德的四因說,能不能解說這個『忒修斯之船』的同一性問題呢?也許先讓我們聽聽孔老夫子的『觚之抱怨』吧!
《倫语‧雍也》:
子曰:觚不觚,觚哉!觚哉!
朱熹集注:觚,棱也;或曰酒器,或曰木簡,皆器之有棱者也。不觚者,蓋當時失其制而不為棱也。觚哉:觚哉!言不得為觚也。
從造字來講,『觚』字也有『棱角』的啊,竟然將『方』觚改為『圓』觚!無怪乎孔老夫子會喊著『這算是個觚嗎』?『這難到也算是個觚嗎』??
因此如果問他老先生這個『忒修斯之船』的問題,也許他會說︰依其『形制』並沒有什麼被『改變』,所以還一樣是『那個』。或許說『形式因』定義著『什麼是什麼』,所以相較之下比它是用『什麼所構成』的『物質因』還來的重要的吧!!
─── 摘自《Thue 之改寫系統《三》》
怎通『透鏡』之『矩陣形式』哩!◎
前三篇文本中,我們談了一般『光學矩陣』
![]()
只要 ![]() ,都可借著『自由空間』
,都可借著『自由空間』
![]()
化成一個等效之『薄透鏡』
![]() 。
。
因此在『主平面』之參考系裡,分享著同樣的『成像公式』
![]()
,具有相同『成像條件』, ![]() 參數為
參數為 ![]()
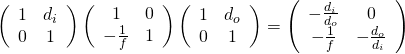 。
。
甚至可以『串接成像』
![]()
的矣!如是就確定了參數 ![]() 之『聚焦』地位,以及參數
之『聚焦』地位,以及參數 ![]() 的『影像縮放』性質!!若問為什麼『平面鏡』是理想成像系統的呢?難到原因在於『反射』與『折射』不同耶??但思
的『影像縮放』性質!!若問為什麼『平面鏡』是理想成像系統的呢?難到原因在於『反射』與『折射』不同耶??但思
【曲面折射】
![]() 和
和
【曲面反射】
![]()
當 ![]() 時,參數
時,參數 ![]() 趨近於零﹐等同於『平面』
趨近於零﹐等同於『平面』
【平面折射】
![]() 和
和
【平面反射】
![]() 的哩。
的哩。
那為何維基百科特別註記『平面反射』之說明為
Only valid for mirrors perpendicular to the ray.
的呢!!??問題在『小角度』近軸近似下,實在無法表象『任意角度』都能『完美成像』之『理想平面鏡』呀??!!