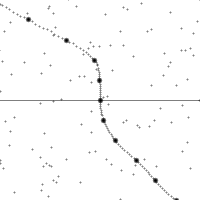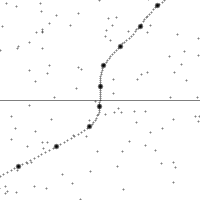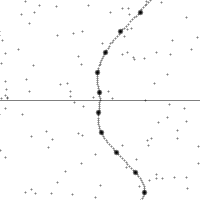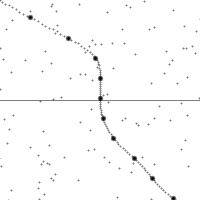
一次再次閱讀相同的文章,令人驚訝的是次次理解都不同◎
《如何閱讀□○??》
一九四零年,美國哲學家莫蒂默‧傑爾姆‧阿德勒 Mortimer Jerome Adler 寫了一本《如何閱讀一本書》的書。其後於一九七二年,美國哥倫比亞大學的教授查爾斯‧范多倫 Charles Van Doren 重新修訂。這本書主要論述如何『通過閱讀』增進『理解力』。《如何閱讀一本書》將閱讀分做四個層次『基礎閱讀』、『檢視閱讀』、『分析閱讀』和『主題閱讀』。並在書後推薦了一系列的『經典名著』。『 目的』是強調閱讀是一種『自主活動』。
其實『知識』如同『蛛網』,經由各種『學習渠道』與『自身經驗』,逐步建立起來。果真能像『蜘蛛』一樣,牽一髮而動全身的去『捕捉』,又何止是談『閱讀』一本書?智慧不只可以『閱讀』一個『時代』! 更能夠『閱讀』整個『自然』與『社會』的啊!!
來來回回又回到『透視性』之『抽象』定義︰
Projective geometry
In projective geometry the points of a line are called a projective range, and the set of lines in a plane on a point is called a pencil.
Given two lines and
in a plane and a point P of that plane on neither line, the bijective mapping between the points of the range of
and the range of
determined by the lines of the pencil on P is called a perspectivity (or more precisely, a central perspectivity with center P).[4] A special symbol has been used to show that points X and Y are related by a perspectivity;
In this notation, to show that the center of perspectivity is P, write
Using the language of functions, a central perspectivity with center P is a function
(where the square brackets indicate the projective range of the line) defined by
.[5] This map is an involution, that is,
.
The existence of a perspectivity means that corresponding points are in perspective. The dual concept, axial perspectivity, is the correspondence between the lines of two pencils determined by a projective range.
既已有了『賦值』辦法、『定位』方案
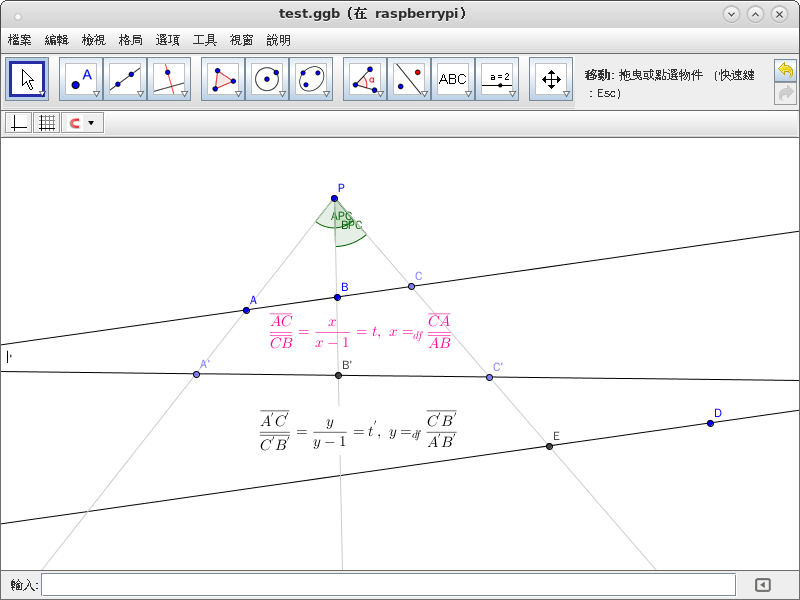
,那麼 ![]() 將如何『表達』呢?
將如何『表達』呢?
假設
![]() ,
, ![]() ,
, ![]()
![]() 是線
是線 ![]() 上的『單位長度』,任意一點
上的『單位長度』,任意一點 ![]() 之『賦值』為
之『賦值』為 ![]()
![]() 。對應之
。對應之
![]() 是線
是線 ![]() 上的『單位長度』,任意一點
上的『單位長度』,任意一點 ![]() 之『賦值』為
之『賦值』為 ![]()
![]()
依據『幾何事實』
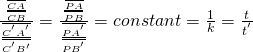 ,因此
,因此
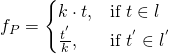 。
。
為什麼 ![]() 彷彿『 case by case 』耶??因為
彷彿『 case by case 』耶??因為
![]() 辭義使然。如是當然
辭義使然。如是當然
![]() 乎!!
乎!!
此處 ![]() 與
與 ![]() 似乎有『簡單』『線性』關係◎
似乎有『簡單』『線性』關係◎
如果選擇 ![]() 來描述,已知
來描述,已知
![]() 。那麼
。那麼
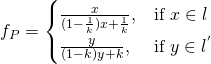 。
。
不單『非線性』而且『複雜』的哩★
宛如『投影』概念之『相對論』呀☆
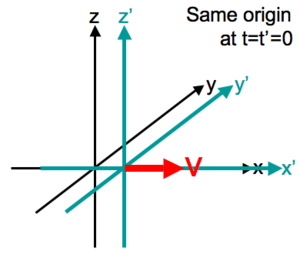
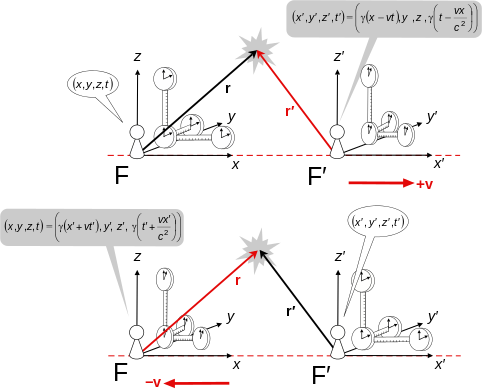
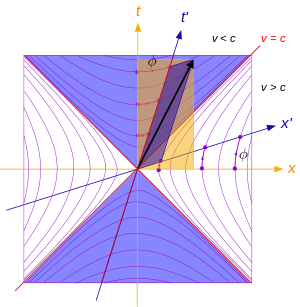
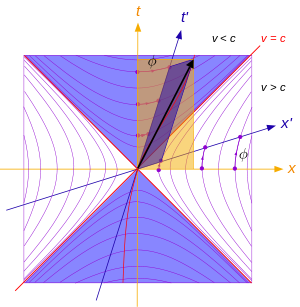
『運動是第一義』它意指什麼的呢?如果考察人們對『時間』的『認識』,總離不開對物體『運動』的『觀察』。之前在《時間是什麼??》一文裡,我們談到了『古典物理』是以『牛頓第一運動定律』所指稱的『慣性座標系觀察者』之『時空觀』為『基礎』的。『牛頓』假設『存在』一個對所有的『慣性座標系』中『觀察者』都『相同』並且『恆定恆速』的『時間之流』,自此『時間』就成為『第一義』的了。也就是說如果『□觀察者』說『兩事件』『同時發生』,『○觀察者』也講那『兩事件』『同時發生』。因而『第一運動定律』── 假使沒有外力作用,靜者恆靜,動者作等速直線運動,在『第二運動定律』的強大光芒『覆照』下,反倒顯得晦暗不明的了,宛如是個『力等於零』的『特例』一般。於是『速度』 ![]() 的『定義』
的『定義』 ![]() 與『相對速度』是
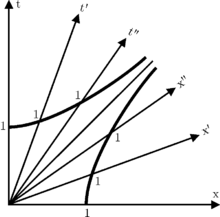
與『相對速度』是 ![]() 的『兩』個『慣性座標系』彷彿是『同義語』。殊不知這個『相對速度』是『兩』個『觀察者』之『互見』,而且『運動方向』相反,並不能『自見』的啊!要是說果真能夠『自見』又豈會自己『無法度量』的呢?於是乎有『無窮多』個『慣性觀察者』各以『無限種』之『相對速度』『運動』,然而他們所『觀察到』的『自然律』都是一樣的,這就是『慣性』的『本義』。其實『觀察者』之『概念』有一點像『抽象擬人化』的說法,比方說,一個『對我而言』運動中的『粒子』,在『粒子』自己的『慣性座標系』裡,『自然律』一樣的『適用』。如此『對我而言』可用『我的時空』將那個『粒子』標示在『我的時空圖』
的『兩』個『慣性座標系』彷彿是『同義語』。殊不知這個『相對速度』是『兩』個『觀察者』之『互見』,而且『運動方向』相反,並不能『自見』的啊!要是說果真能夠『自見』又豈會自己『無法度量』的呢?於是乎有『無窮多』個『慣性觀察者』各以『無限種』之『相對速度』『運動』,然而他們所『觀察到』的『自然律』都是一樣的,這就是『慣性』的『本義』。其實『觀察者』之『概念』有一點像『抽象擬人化』的說法,比方說,一個『對我而言』運動中的『粒子』,在『粒子』自己的『慣性座標系』裡,『自然律』一樣的『適用』。如此『對我而言』可用『我的時空』將那個『粒子』標示在『我的時空圖』 ![]() 上,一個與『粒子偕行』相對『靜止』的『觀察者』,就把『我的運動』畫在『他的時空圖』
上,一個與『粒子偕行』相對『靜止』的『觀察者』,就把『我的運動』畫在『他的時空圖』 ![]() 上的了。這個『互為動靜』的『論述』就是『相對運動』的『實質』,並不存在『絕對運動』的啊。所以『我說』『那個粒子』在
上的了。這個『互為動靜』的『論述』就是『相對運動』的『實質』,並不存在『絕對運動』的啊。所以『我說』『那個粒子』在 ![]() 『時刻』『接近』
『時刻』『接近』 ![]() 『位置』,當
『位置』,當 ![]() 『時』『到達』
『時』『到達』 ![]() 『處』,於
『處』,於 ![]() 『之後』『離開』
『之後』『離開』 ![]() 『之地』,『我』將此『等速運動』歸之於『粒子』的『運動慣性』;那個與『粒子偕行』相對『靜止』的『觀察者』亦將此『等速運動』歸之於『我』的『運動慣性』,這就是『運動』之『慣性』的『第一義』。所謂『飛鳥之景未嘗動也,鏃矢之疾而有不行不止之時』是不了解『慣性之意』『跳躍』於『互為動靜』之間,事實上對『任一方』而言,那個『相對運動』都是『存在的』,根本不會有『瞬時速度』存不存在的問題,所以才名之為『慣性定律』︰
『之地』,『我』將此『等速運動』歸之於『粒子』的『運動慣性』;那個與『粒子偕行』相對『靜止』的『觀察者』亦將此『等速運動』歸之於『我』的『運動慣性』,這就是『運動』之『慣性』的『第一義』。所謂『飛鳥之景未嘗動也,鏃矢之疾而有不行不止之時』是不了解『慣性之意』『跳躍』於『互為動靜』之間,事實上對『任一方』而言,那個『相對運動』都是『存在的』,根本不會有『瞬時速度』存不存在的問題,所以才名之為『慣性定律』︰ ![]() ,或者比喻的說︰在牛頓力學裡,沒有任何東西能夠阻擋『恆定恆速』之『時間之流』的啊!!
,或者比喻的說︰在牛頓力學裡,沒有任何東西能夠阻擋『恆定恆速』之『時間之流』的啊!!
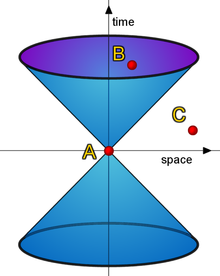
當『愛因斯坦』假設了『光速』對所有的『慣性觀察者』都是『一樣的』之後,引申出了『同時性的破壞』、『運動的鐘會變慢』、『運動的尺會縮短』…等等的『大哉論』,人們開始恍然大悟所謂的『相對』、所見的『運動』…之種種必須以『量測方法』為依據,面對『大自然』的『事實』並沒有『純粹思辯』所得之理『一定對』之『位置』的吧!
─── 摘自《【Sonic π】電聲學之電路學《四》之《 !!!! 》下》