2 | 10 月 | 2017 | FreeSandal

待船停妥，終於登上了平台。這湖心小築上圓小下方大，不知是否是象徵『地包天』的呢？突然吹來一陣霧氣，在月光照耀下，彷彿有道『彩虹』，卻看不清楚。一時霧更濃了，『邀請護照』正閃爍

的圖案。

在 Mrphs 催促下，趕緊進到了小築的大廳。只見他一直向著東邊走，在好大一片落地景觀窗前，忽見那

『幻月』掛空中。

原本以為發生什麼危險，所以急行，此時只是驚訝『幻月』之美，難以形容。 Mrphs 開口說道︰先生『神行』不覺溫度陡降氣壓突變。一般此時『秋雪』早來，由於湖水『鹽度』從南至北梯減，往常日湖北已經結冰，正向南擴大之中。今年氣象又變，據新數據推斷『秋雪』將延一『』旬，大約十天左右。或因為已經多次聽聞這『秋雪』之詞，總覺困惑，問曰︰什麼是『秋雪』的呢？ Mrphs 說︰現今氣候只有『夏‧冬』交替，急徐不定，長短不一，其實『春‧秋』早就名存實亡了。懷念之故，用『秋雪』表示初冬之雪而已。方才『冰晶』突起，『邀請護照』上有多種『氣象』感測器，可以補足『 It 網』之『氣候大數據』，用本地『即時資訊』推斷天氣變化，所以知道『冰晶』將臨，很可能看得到『幻月』。當下 Mrphs 在『邀請護照』上按了按，螢幕上顯現

『冰晶』影像。

《勇闖新世界︰ W!o《卡夫卡村》變形祭︰感知自然‧尖端‧一》

時近中秋，月分外明矣。當此情境，懸想

思維如有內核鉤深索隱，將生結晶乎？

恰似波利亞所說者耶！

回神看著塗鴉手稿，寫著

假設 $z_{\alpha}(t)$ 、 $z_{\beta}(t)$ 是複平面上任意兩條曲線之參數方程

參數方程和函數很相似：它們都是由一些在指定的集的數，稱為參數或自變數，以決定因變數的結果。例如在運動學，參數通常是「時間」，而方程的結果是速度、位置等。

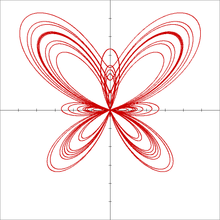
一般地，在平面直角座標系中，如果曲線上任意一點的座標x、y都是某個變數t的函數： ${\begin{cases}x=f(t)\\y=g(t)\end{cases}}$ ，並且對於t的每一個允許的取值，由方程組確定的點(x, y)都在這條曲線上，那麼這個方程就叫做曲線的參數方程，聯繫變數x、y的變數t叫做參變數，簡稱參數。相對而言，直接給出點座標間關係的方程叫普通方程。

用參數方程可以很容易表示出的蝶形線

如果它們在 $t_0$ 時，相交於 $z_0$ ︰

$z_0 = z_{\alpha}(t_0) = z_{\beta}(t_0)$ 。

那麼任一 $z^{'} = h(z)$ 形式之變換，終將之映射至 $z_{\alpha}^{'} (t)$ 、 $z_{\beta}^{'}(t)$ 也。此時兩線會交於 $z_0^{'} = h(z_0)$ 矣。如是

$\frac{d}{dt} z^{'} (t) = \frac{d}{dz} h(z) \cdot \frac{d}{dt} z(t)$

就 $z_0 = x_{\alpha}(t_0) = x_{\beta}(t_0)$ 而言，是說

$\frac{d}{dt} z^{'} (t) |_{t=t_0} = \frac{d}{dz} h(z) |_{z=z_0} \cdot \frac{d}{dt} z(t) |_{t=t_0}$ 呦！！

承上篇，豈能不保角嗎？？

反倒好奇萬花尺在保型變換下的模樣哩◎

內旋輪線參數方程式參考圖

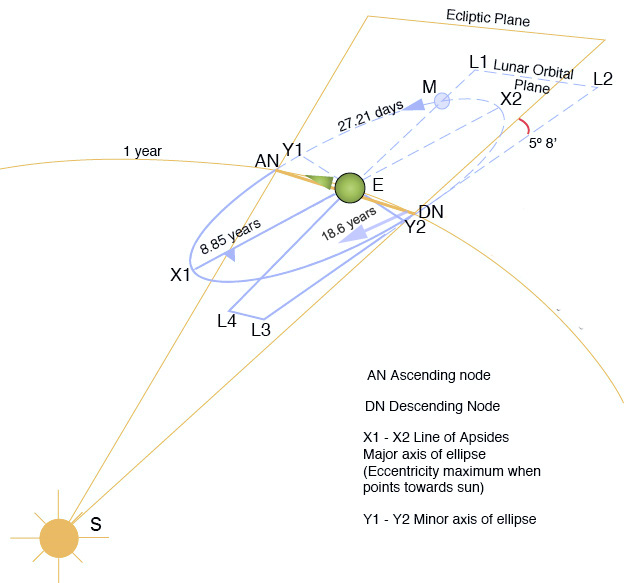
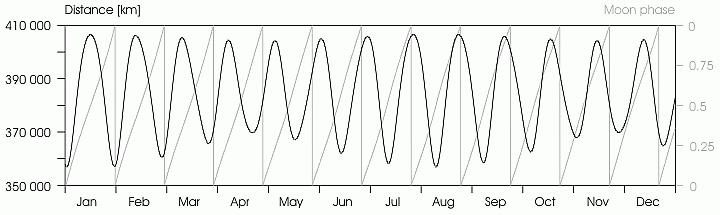
地球繞著太陽轉，月亮繞著地球轉。兩個週期運動耦合起來，卻是複雜萬端。月球軌道以二十七點三二天環繞地球一周。地球和月球的質心在距地心四千七百公里處，各自圍繞著質心運轉。月球與地球中心的平均距離是三十八萬五千公里，約為地球半徑的六十倍。軌道的平均速度是一千零二十三公里／秒，月球在恆星背景上大約每小時移動 0.5°，軌道的平均離心率是0.0549。非圓形的軌道導致從大地上賞月時，視直徑的大小和角速度上都有著顯著的變化。對一位假想在質心上的觀測者而言，月球每天的平均角位移量是向東 13. 176358°，然而軌道的指向在空間中卻不固定，而是隨著時間不斷的進動；其一是拱點線的進動，橢圓形的月球軌道慢慢的逆時鐘方向轉動，一周需要三千兩百三十三天。另一是月球軌道與黃道的交點對的進動，一圈長達十八點六年。

果真簡諧運動的耦合，也許是和諧的，未必是簡單的！！

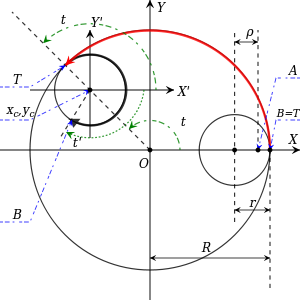
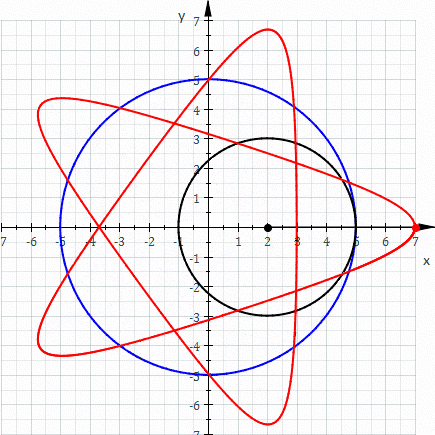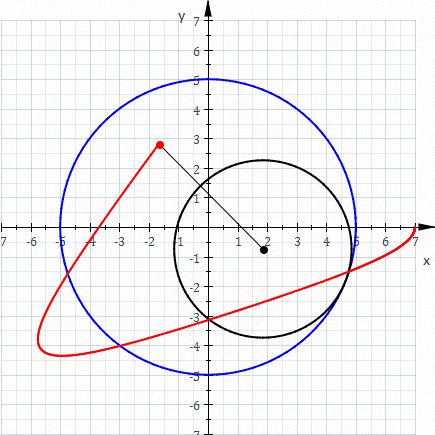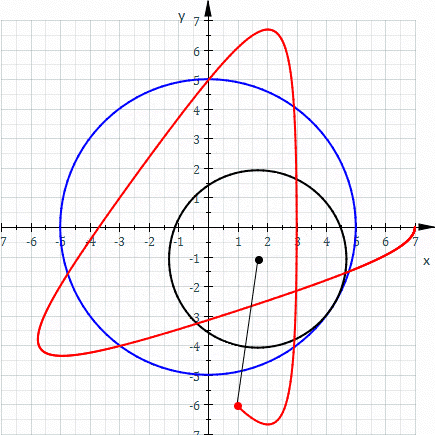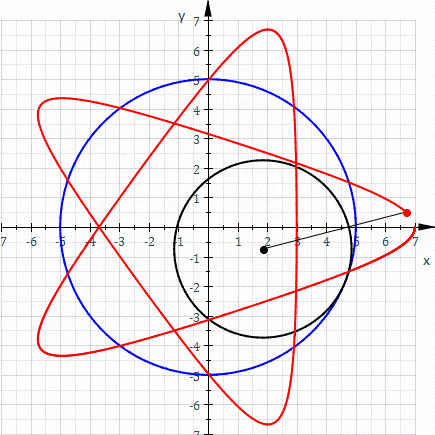
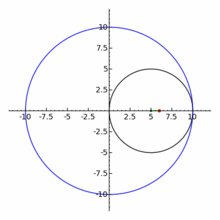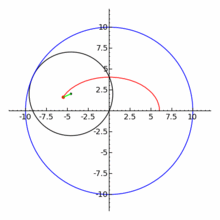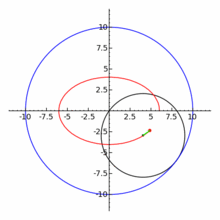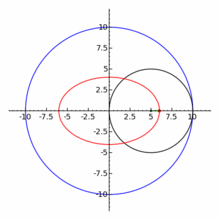
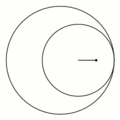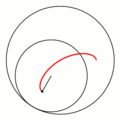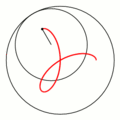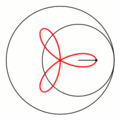
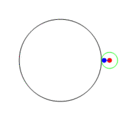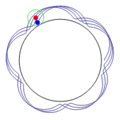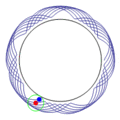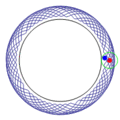
一八八零年代波蘭數學家 Bruno Abakanowicz 發明了『螺旋圖』Spirograph 。一九六四年英國工程師德尼斯‧費舍爾 Denys Fisher 發現使用多種『大小比值』不同的兩個內外『圓形齒輪』，當『內小圓形齒輪』上不同的『筆洞位置』在『外大圓形齒輪』上『循著圓周』轉動時，可以畫出各種美麗的『內旋輪線』 hypotrochoid 以及『外旋輪線 』epitrochoid。在經過一番齒輪『大小比值』與筆洞『位置比值』的研究後，費舍爾於隔年一九六五年的德國 Nuremberg 國際玩具展將之發表上市。由於它所繪出的『圖案』令人聯想到『萬花筒』，所以被我們叫做『萬花尺』。這是一個曾經『流行』過的『益智玩具』，其實它是了解『周期運動』組合的『複雜性』很好的『工具』。萬花尺內旋輪線的參數方程式可以表示為

$\begin{array}{rcl} x(t)&=&R\left[(1-k)\cos t+lk\cos \frac{1-k}{k}t\right] ,\\[4pt] y(t)&=&R\left[(1-k)\sin t-lk\sin \frac{1-k}{k}t\right] .\\\end{array}$