樹莓派、樹莓派之學習、樹莓派之教育

STEM 隨筆︰古典力學︰運動學【二．四C】

2018-03-31 懸鉤子

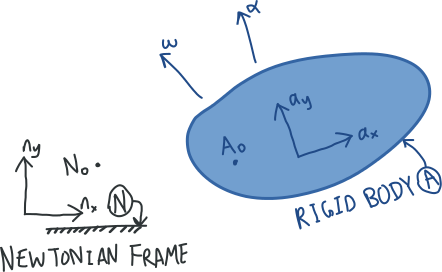
要是不能將相關的『概念』編織『成網』，使之上下聯繫、四通八達，思慮恐泥也！

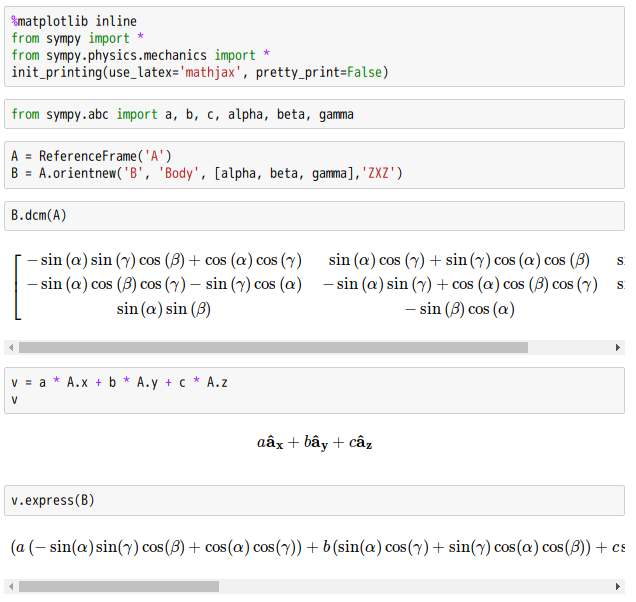
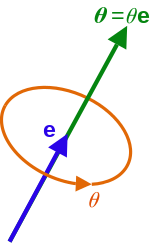
舉例來說︰如何求旋轉矩陣 $R$

$\displaystyle {R = \begin{bmatrix}r_{11}&r_{12}&r_{13}\\r_{21}&r_{22}&r_{23}\\r_{31}&r_{32}&r_{33}\end{bmatrix}}.$

$det(R) = 1, \ R^{T} R = I .$

的旋轉軸呢？

或曰可用『本徵值方程式』 $R \vec{v} = \lambda \vec {v}, \ \lambda = 1$ 解之乎？？

那麼一位親力親為者將可體驗頭暈腦脹呦！！

此處作者假借 SymPy 符號算術略釋此法︰

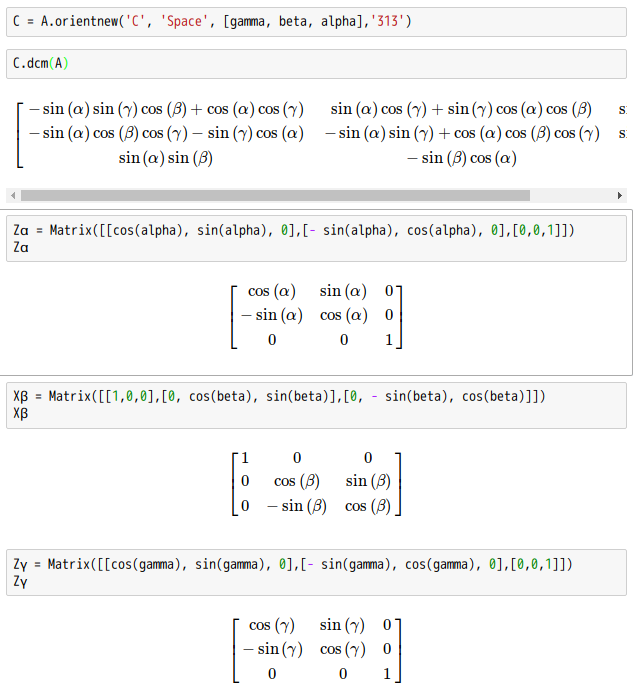
※ 所以用二『歐拉角』不用全，蓋不知 SymPy 要算多久故。

如是一個知道

$\displaystyle \mathbf {R} =\mathbf {I} +(\sin \theta )\mathbf {K} +(1-\cos \theta )\mathbf {K} ^{2}$

的人，深入

Skew-symmetric matrix

In mathematics, particularly in linear algebra, a skew-symmetric (or antisymmetric or antimetric^[1]) matrix is a square matrix whose transpose equals its negative; that is, it satisfies the condition

A^T = −A.

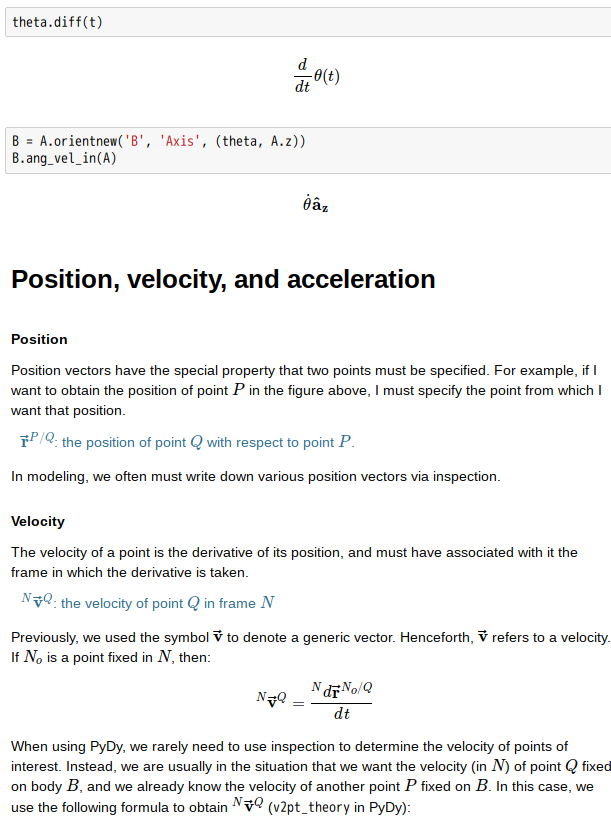
In terms of the entries of the matrix, if a_ij denotes the entry in the i th row and j th column; i.e., A = (a_ij), then the skew-symmetric condition is a_ji = −a_ij. For example, the following matrix is skew-symmetric:

$\displaystyle {\begin{bmatrix}0&2&-1\\-2&0&-4\\1&4&0\end{bmatrix}}.$

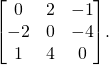
Properties

Throughout, we assume that all matrix entries belong to a field 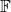$\displaystyle \mathbb {F}$ whose characteristic is not equal to 2: that is, we assume that 1 + 1 ≠ 0, where 1 denotes the multiplicative identity and 0 the additive identity of the given field. If the characteristic of the field is 2, then a skew-symmetric matrix is the same thing as a symmetric matrix.

The sum of two skew-symmetric matrices is skew-symmetric.
A scalar multiple of a skew-symmetric matrix is skew-symmetric.
The elements on the diagonal of a skew-symmetric matrix are zero, and therefore also its trace.
If 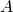$\displaystyle A$ is a skew-symmetric matrix with real entries, i.e., if $\displaystyle \mathbb {F} =\mathbb {R}$ .
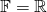If 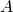$\displaystyle A$ is a real skew-symmetric matrix and 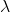$\displaystyle \lambda$ is a real eigenvalue, then $\displaystyle \lambda =0$ .
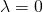If 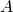$\displaystyle A$ is a real skew-symmetric matrix, then 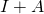$\displaystyle I+A$ is invertible, where 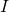$\displaystyle I$ is the identity matrix.

Vector space structure

As a result of the first two properties above, the set of all skew-symmetric matrices of a fixed size forms a vector space. The space of 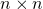$\displaystyle n\times n$ skew-symmetric matrices has dimension n(n−1)/2.

Let Mat_n denote the space of n × n matrices. A skew-symmetric matrix is determined by n(n − 1)/2 scalars (the number of entries above the main diagonal); a symmetric matrix is determined by n(n + 1)/2 scalars (the number of entries on or above the main diagonal). Let Skew_n denote the space of n × n skew-symmetric matrices and Sym_n denote the space of n × n symmetric matrices. If A ∈ Mat_n then

$\displaystyle A={\frac {1}{2}}\left(A-A^{\mathsf {T}}\right)+{\frac {1}{2}}\left(A+A^{\mathsf {T}}\right).$

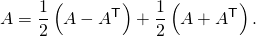
Notice that ½(A − A^T) ∈ Skew_n and ½(A + A^T) ∈ Sym_n. This is true for every square matrix A with entries from any field whose characteristic is different from 2. Then, since Mat_n = Skew_n + Sym_n and Skew_n ∩ Sym_n = {0},

$\displaystyle {\mbox{Mat}}_{n}={\mbox{Skew}}_{n}\oplus {\mbox{Sym}}_{n},$

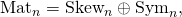
where ⊕ denotes the direct sum.

Denote by 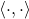$\displaystyle \langle \cdot ,\cdot \rangle$ the standard inner product on Rⁿ. The real n-by-n matrix A is skew-symmetric if and only if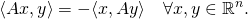

$\displaystyle \langle Ax,y\rangle =-\langle x,Ay\rangle \quad \forall x,y\in {\mathbb {R} }^{n}.$

This is also equivalent to 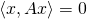$\displaystyle \langle x,Ax\rangle =0$ for all x (one implication being obvious, the other a plain consequence of 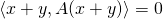$\displaystyle \langle x+y,A(x+y)\rangle =0$ for all x and y). Since this definition is independent of the choice of basis, skew-symmetry is a property that depends only on thelinear operator A and a choice of inner product.

All main diagonal entries of a skew-symmetric matrix must be zero, so the trace is zero. If A = (a_ij) is skew-symmetric, a_ij = −a_ji; hence a_ii = 0.

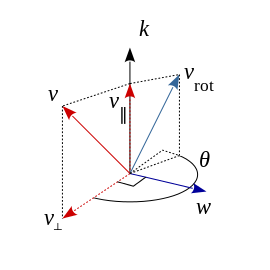
3×3 skew symmetric matrices can be used to represent cross products as matrix multiplications.

Determinant

Let A be a n×n skew-symmetric matrix. The determinant of A satisfies

det(A^T) = det(−A) = (−1)ⁿdet(A).

In particular, if n is odd, and since the underlying field is not of characteristic 2, the determinant vanishes. Hence, all odd dimension skew symmetric matrices are singular as their determinants are always zero. This result is called Jacobi’s theorem, after Carl Gustav Jacobi (Eves, 1980).

The even-dimensional case is more interesting. It turns out that the determinant of A for n even can be written as the square of a polynomial in the entries of A, which was first proved by Cayley:^[2]

det(A) = Pf(A)².

This polynomial is called the Pfaffian of A and is denoted Pf(A). Thus the determinant of a real skew-symmetric matrix is always non-negative. However this last fact can be proved in an elementary way as follows: the eigenvalues of a real skew-symmetric matrix are purely imaginary (see below) and to every eigenvalue there corresponds the conjugate eigenvalue with the same multiplicity; therefore, as the determinant is the product of the eigenvalues, each one repeated according to its multiplicity, it follows at once that the determinant, if it is not 0, is a positive real number.

The number of distinct terms s(n) in the expansion of the determinant of a skew-symmetric matrix of order n has been considered already by Cayley, Sylvester, and Pfaff. Due to cancellations, this number is quite small as compared the number of terms of a generic matrix of order n, which is n!. The sequence s(n) (sequence A002370 in the OEIS) is

1, 0, 1, 0, 6, 0, 120, 0, 5250, 0, 395010, 0, …

and it is encoded in the exponential generating function

$\displaystyle \sum _{n=0}^{\infty }{\frac {s(n)}{n!}}x^{n}=(1-x^{2})^{-{\frac {1}{4}}}\exp \left({\frac {x^{2}}{4}}\right).$

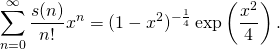
The latter yields to the asymptotics (for n even)

$\displaystyle s(n)=\pi ^{-{\frac {1}{2}}}2^{\frac {3}{4}}\Gamma \left({\frac {3}{4}}\right)\left({\frac {n}{e}}\right)^{n-{\frac {1}{4}}}\left(1+O\left({\frac {1}{n}}\right)\right).$

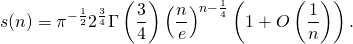
The number of positive and negative terms are approximatively a half of the total, although their difference takes larger and larger positive and negative values as n increases (sequence A167029 in the OEIS).

Cross product

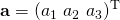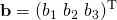Three-by-three skew-symmetric matrices can be used to represent cross products as matrix multiplications. Consider vectors $\displaystyle \mathbf {a} =(a_{1}\ a_{2}\ a_{3})^{\mathrm {T} }$ and $\displaystyle \mathbf {b} =(b_{1}\ b_{2}\ b_{3})^{\mathrm {T} }$ . Then, defining matrix:

$\displaystyle [\mathbf {a} ]_{\times }={\begin{bmatrix}\,\,0&\!-a_{3}&\,\,\,a_{2}\\\,\,\,a_{3}&0&\!-a_{1}\\\!-a_{2}&\,\,a_{1}&\,\,0\end{bmatrix}}$

the cross product can be written as

$\displaystyle \mathbf {a} \times \mathbf {b} =[\mathbf {a} ]_{\times }\mathbf {b}$

This can be immediately verified by computing both sides of the previous equation and comparing each corresponding element of the results.

One actually has

$\displaystyle [\mathbf {a\times b} ]_{\times }=[\mathbf {a} ]_{\times }[\mathbf {b} ]_{\times }-[\mathbf {b} ]_{\times }[\mathbf {a} ]_{\times };$

i.e., the commutator of skew-symmetric three-by-three matrices can be identified with the cross-product of three-vectors. Since the skew-symmetric three-by-three matrices are the Lie algebra of the rotation group 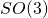$\displaystyle SO(3)$ this elucidates the relation between three-space 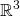$\displaystyle \mathbb {R} ^{3}$ , the cross product and three-dimensional rotations. More on infinitesimal rotations can be found below.

以及

Cross product

In mathematics and vector algebra, the cross product or vector product (occasionally directed area product to emphasize the geometric significance) is a binary operation on two vectors in three-dimensional space (R³) and is denoted by the symbol ×. Given twolinearly independent vectors a and b, the cross product, a × b, is a vector that is perpendicular to both a and b and thus normal to the plane containing them. It has many applications in mathematics, physics, engineering, and computer programming. It should not be confused with dot product (projection product).

If two vectors have the same direction (or have the exact opposite direction from one another, i.e. are not linearly independent) or if either one has zero length, then their cross product is zero. More generally, the magnitude of the product equals the area of aparallelogram with the vectors for sides; in particular, the magnitude of the product of two perpendicular vectors is the product of their lengths. The cross product is anticommutative (i.e., a × b = −(b × a)) and is distributive over addition (i.e.,a × (b + c) = a × b + a × c). The space R³ together with the cross product is an algebra over the real numbers, which is neither commutative nor associative, but is a Lie algebra with the cross product being the Lie bracket.

Like the dot product, it depends on the metric of Euclidean space, but unlike the dot product, it also depends on a choice of orientation or “handedness“. The product can be generalized in various ways; it can be made independent of orientation by changing the result to pseudovector, or in arbitrary dimensions the exterior product of vectors can be used with a bivector or two-form result. Also, using the orientation and metric structure just as for the traditional 3-dimensional cross product, one can in n dimensions take the product ofn − 1 vectors to produce a vector perpendicular to all of them. But if the product is limited to non-trivial binary products with vector results, it exists only in three and seven dimensions.^[1] If one adds the further requirement that the product be uniquely defined, then only the 3-dimensional cross product qualifies. (See § Generalizations, below, for other dimensions.)

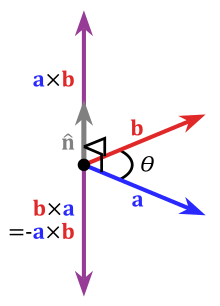
The cross product in respect to a right-handed coordinate system

Definition

The cross product of two vectors a and b is defined only in three-dimensional space and is denoted by a × b. In physics, sometimes the notation a ∧ b is used,^[2] though this is avoided in mathematics to avoid confusion with theexterior product.

The cross product a × b is defined as a vector c that is perpendicular (orthogonal) to both a and b, with a direction given by the right-hand rule and a magnitude equal to the area of the parallelogram that the vectors span.

The cross product is defined by the formula^[3]^[4]

$\displaystyle \mathbf {a} \times \mathbf {b} =\left\|\mathbf {a} \right\|\left\|\mathbf {b} \right\|\sin(\theta )\ \mathbf {n}$

where θ is the angle between a and b in the plane containing them (hence, it is between 0° and 180°), ‖a‖ and ‖b‖ are the magnitudes of vectors a and b, and n is a unit vector perpendicular to the plane containing a and bin the direction given by the right-hand rule (illustrated). If the vectors a and b are parallel (i.e., the angle θ between them is either 0° or 180°), by the above formula, the cross product of a and b is the zero vector 0.

By convention, the direction of the vector n is given by the right-hand rule, where one simply points the forefinger of the right hand in the direction of a and the middle finger in the direction of b. Then, the vector n is coming out of the thumb (see the picture on the right). Using this rule implies that the cross product is anti-commutative, i.e., b × a = −(a × b). By pointing the forefinger toward b first, and then pointing the middle finger toward a, the thumb will be forced in the opposite direction, reversing the sign of the product vector.

Using the cross product requires the handedness of the coordinate system to be taken into account (as explicit in the definition above). If a left-handed coordinate system is used, the direction of the vector n is given by the left-hand rule and points in the opposite direction.

This, however, creates a problem because transforming from one arbitrary reference system to another (e.g., a mirror image transformation from a right-handed to a left-handed coordinate system), should not change the direction of n. The problem is clarified by realizing that the cross product of two vectors is not a (true) vector, but rather a pseudovector. See cross product and handedness for more detail.

Names

According to Sarrus’s rule, the determinant of a 3×3 matrix involves multiplications between matrix elements identified by crossed diagonals

In 1881, Josiah Willard Gibbs, and independently Oliver Heaviside, introduced both the dot product and the cross product using a period (a . b) and an “x” (a x b), respectively, to denote them.^[5]

In 1877, to emphasize the fact that the result of a dot product is a scalar while the result of a cross product is a vector, William Kingdon Clifford coined the alternative namesscalar product and vector product for the two operations.^[5] These alternative names are still widely used in the literature.

Both the cross notation (a × b) and the name cross product were possibly inspired by the fact that each scalar component of a × b is computed by multiplying non-corresponding components of a and b. Conversely, a dot product a ⋅ b involves multiplications between corresponding components of a and b. As explained below, the cross product can be expressed in the form of a determinant of a special 3 × 3 matrix. According to Sarrus’s rule, this involves multiplications between matrix elements identified by crossed diagonals.

之後，將會 …… 耶☆

樹莓派、樹莓派之學習、樹莓派之教育

STEM 隨筆︰古典力學︰運動學【二．四B】

2018-03-30 懸鉤子

生於一八四八年十一月八日的弗里德里希‧路德維希‧戈特洛布‧弗雷格 Friedrich Ludwig Gottlob Frege 德國數學、邏輯和哲學大家，是近代數理邏輯和分析哲學的主要奠基人。享壽七十八年，其子皆不幸早逝，最終於五十八歲時領養了一子。時年二十二歲進耶拿大學修習，兩年後轉進哥廷根，二十六歲時取得數學哲學博士學位，兩年後他回耶拿擔任講師，三十二歲時就任助理教授，四十九歲成為教授。或因其父擅長數學亦任教於校，早年弗雷格研究數學和歐氏幾何學，深感亞里斯多德的邏輯不足以解釋幾何學，根本上很難處理『有一些』與『所有的』這樣的一些『量詞』，於是開始深研邏輯。一八七九年出版了一本名為『概念文字』── Begriffsschrift ──的書，書名副題是『模仿算術純思維之形式語言』，無疑是西方新邏輯學之開山之作。有人說他的形式邏輯系統之想法或得之於萊布尼茲對『運算推論機械』之渴望。其後又於一八八四年出版了《算術之基礎 ── 數之概念邏輯數學研究》，之後於一八九三年發行《算術之基本規律》卷一，這部書用著『集合論』演繹算術，或因卷二考慮自行發售之故，那時卻得英國伯特蘭·羅素回覆來的一封信，讀後大吃一驚，遂於一九零二年六月二十二日立即回覆，見之左圖。此事故因他先前寫給羅素的信上提到為著他的算術之基本規律所構造的一個『特殊的集合』，它由所有不包括自己為元素的一切集合所構成，或可用今天的符號說 S = {x|x ∉ x}，於是羅素便問著那樣 S 屬不屬於 S 呢？只是此時卷二也已然付印，弗雷格於是也祇能在書中加個『後記』以示這事，慨嘆的回信給羅素說︰以為剛將完成之際卻發現那個大厦的基石已然動搖，這對於一個科學的工作者來說，沒有什麼能比這個更不幸的了！！

這就是史稱的『羅素悖論』，之後又叫做『理髮師悖論』，有著許多的版本，其一寫道︰

有一位理髮師宣稱，他為所有不為自己理髮的人理髮，請問他為不為自己理髮？

相傳弗雷格在耶拿大學時僅有一個學生 Rudolf Carnap ；他於有生之年從未得到廣泛的贊譽，即使羅素和維根斯坦都曾大力讚揚他，還是因著第二次世界大戰之後，部分德國的哲學家和邏輯學家移居到了美國，以及嫡傳弟子卡爾納普的宣傳才在英語世界裡廣為人知，那些瞭解和尊敬弗雷格之人才將他一生的主要著作翻譯成了英文。！！

古來就有『晨星』『暮星』之惑；當日太白金星之為天神。又以朝見於東謂之『啟明』，夕位於西而曰『太白』，主殺伐。此事故東西皆然，祇可抱之以微笑 Smile 了！！

由於人們對於語言文字習以為常，以至於論述時其『所指』到底『存在』或是『不存在』反而不甚了了了。比方說吧

白色的念頭躺在茵茵的草地上

，這句話要作何解釋？如果用下面的議論可以嗎？

白色的念頭在我的腦海裡，我躺在茵茵的草地上之故。

─── 《{X|X ∉ X} ！！？？》

『剛體』

Rigid body

In physics, a rigid body is a solid body in which deformation is zero or so small it can be neglected. The distance between any two given points on a rigid body remains constant in time regardless of external forces exerted on it. A rigid body is usually considered as a continuous distribution of mass.

In the study of special relativity, a perfectly rigid body does not exist; and objects can only be assumed to be rigid if they are not moving near the speed of light. In quantum mechanics a rigid body is usually thought of as a collection of point masses. For instance, in quantum mechanics molecules (consisting of the point masses: electrons and nuclei) are often seen as rigid bodies (see classification of molecules as rigid rotors).

之概念其實古就萌芽，歐拉的旋轉定理

歐拉旋轉定理

在運動學裏，歐拉旋轉定理(Euler’s rotation theorem)表明，在三維空間裏，假設一個剛體在做一個位移的時候，剛體內部至少有一點固定不動，則此位移等價於一個繞著包含那固定點的固定軸的旋轉。這定理是以瑞士數學家萊昂哈德·歐拉命名。於1775年，歐拉使用簡單的幾何論述證明了這定理。

用數學術語，在三維空間內，任何共原點的兩個座標系之間的關係，是一個繞著包含原點的固定軸的旋轉。這也意味著，兩個旋轉矩陣的乘積還是旋轉矩陣。一個不是單位矩陣的旋轉矩陣必有一個實值的本徵值，而這本徵值是 1 。對應於這本徵值的本徵向量就是旋轉所環繞的固定軸^[1]。

使得一般固體物可用『平移』與『旋轉』向量 ── 最多六個自由度 ── 來描述其運動︰

自由度 (物理學)

在力學裡，自由度指的是力學系統的獨立坐標的個數。力學系統由一組坐標來描述。比如一個質點的三維空間中的運動，在笛卡爾坐標系中，由 $\displaystyle x,\ y,\ z\,$ 三個坐標來描述；或者在球坐標系中，由 $\displaystyle r,\ \theta ,\ \phi \,$ 三個坐標描述。描述系統的坐標可以自由的選取，但獨立坐標的個數總是一定的，即系統的自由度。一般而言， $N$ 個質點組成的力學系統由 $3N$ 個坐標來描述。但力學系統中常常存在著各種約束，使得這 $3N$ 個坐標並不都是獨立的。對於 $N$ 個質點組成的力學系統，若存在 $m$ 個完整約束，則系統的自由度減為

$\displaystyle S=3N-m\,$

比如，運動於平面的一個質點，其自由度為 2。又或是，在空間中的兩個質點，中間以線連接。所以其自由度

$\displaystyle {\begin{aligned}S&=3\times 2-1\\&=3+2+0\end{aligned}}$

其中的3表示2個質點的質心有3個位移方向，但由於有一條線約束，兩個質點繞質心的轉動自由度由3減為2，即不可做以線為軸的轉動，而又由於線是剛性不可伸縮的，故兩質點不可在線的方向上振動，即振動自由度為0。如果線是彈性的，則這個模型類似於兩原子構成的氣體分子模型，除了有3個位移自由度、2個轉動自由度外，還有1個振動自由度。

因此在研究氣體分子時一般將自由度分為平移自由度，轉動自由度及振動自由度三類。

為什麼『狹義相對論』宣稱不存在『完美剛體』呢？

絕非因為傳說愛因斯坦想像『馭光而行』所發現的！

且不論以接近光速『平移』 ── 各點速度都一樣 ── 人類能否存活？？一個高速『旋轉』的東西，視其大小，外緣恐或超過光速矣！！既依據『狹義相對論』講無物可以『超光速』而行，故而過程中蓋早已碎裂也！！◎ 該如何說『完美剛體』之概念呦？？◎

如是假設『宇宙大霹靂』時就有『起始角動量』，那麼其後形成之『銀河規模』會不受限乎？！★

『做人』及『學問』都在道理『前後一貫』的啊！？☆

『什麼是旋轉』 ── 保長保角的變換 ── 之『定義』實已蘊涵『旋轉矩陣』 $R$ 滿足

$\displaystyle \mathbf {R} ^{\mathsf {T}}\mathbf {R} =\mathbf {R} \mathbf {R} ^{\mathsf {T}}=\mathbf {I} ,$

『性質』矣。◎

※ 提示

Dot product

Definition

The dot product may be defined algebraically or geometrically. The geometric definition is based on the notions of angle and distance (magnitude of vectors). The equivalence of these two definitions relies on having a Cartesian coordinate system for Euclidean space.

In modern presentations of Euclidean geometry, the points of space are defined in terms of their Cartesian coordinates, and Euclidean space itself is commonly identified with the real coordinate space Rⁿ. In such a presentation, the notions of length and angles are defined by means of the dot product. The length of a vector is defined as the square root of the dot product of the vector by itself, and the cosine of the (non oriented) angle of two vectors of length one is defined as their dot product. So the equivalence of the two definitions of the dot product is a part of the equivalence of the classical and the modern formulations of Euclidean geometry.

Algebraic definition

The dot product of two vectors a = [a₁, a₂, …, a_n] and b = [b₁, b₂, …, b_n] is defined as:^[1]

$\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}$

where Σ denotes summation and n is the dimension of the vector space. For instance, in three-dimensional space, the dot product of vectors [1, 3, −5] and [4, −2, −1] is:

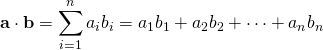
$\displaystyle {\begin{aligned}\ [1,3,-5]\cdot [4,-2,-1]&=(1)(4)+(3)(-2)+(-5)(-1)\\&=4-6+5\\&=3\end{aligned}}$

The dot product can also be written as:

$\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {a} ^{T}\mathbf {b}$ .

Here, $\displaystyle \mathbf {a} ^{T}$ means the transpose of $\displaystyle \mathbf {a}$ $\mathbf {a}$ .

Using the above example, a 1 × 3 matrix (row vector) is multiplied by a 3 × 1 matrix (column vector) to get the result (1 × 1 matrix is obtained by matrix multiplication, which is a scalar):

$\displaystyle {\begin{bmatrix}1&3&-5\end{bmatrix}}{\begin{bmatrix}4\\-2\\-1\end{bmatrix}}=3$ .

Geometric definition

In Euclidean space, a Euclidean vector is a geometric object that possesses both a magnitude and a direction. A vector can be pictured as an arrow. Its magnitude is its length, and its direction is the direction that the arrow points. The magnitude of a vector a is denoted by $\displaystyle \left\|\mathbf {a} \right\|$ . The dot product of two Euclidean vectors a and b is defined by^[2]^[3]

$\displaystyle \mathbf {a} \cdot \mathbf {b} =\|\mathbf {a} \|\ \|\mathbf {b} \|\cos(\theta ),$

where θ is the angle between a and b.

In particular, if a and b are orthogonal, then the angle between them is 90° and

$\displaystyle \mathbf {a} \cdot \mathbf {b} =0.$

At the other extreme, if they are codirectional, then the angle between them is 0° and

$\displaystyle \mathbf {a} \cdot \mathbf {b} =\left\|\mathbf {a} \right\|\,\left\|\mathbf {b} \right\|$

This implies that the dot product of a vector a with itself is

$\displaystyle \mathbf {a} \cdot \mathbf {a} =\left\|\mathbf {a} \right\|^{2},$

which gives

$\displaystyle \left\|\mathbf {a} \right\|={\sqrt {\mathbf {a} \cdot \mathbf {a} }},$

the formula for the Euclidean length of the vector.

『旋轉』意義︰

$\forall u , \forall v \ u^{T} v {=}_{df} {(R u)}^{T} (R v) = u^{T} R^{T} R v = u^{T} (R^{T} R) v$

樹莓派、樹莓派之學習、樹莓派之教育

STEM 隨筆︰古典力學︰運動學【二．四A】

2018-03-29 懸鉤子

如何認識一個重要的『定理』︰

歐拉旋轉定理

A rotation represented by an Euler axis and angle.

透過『跨文本』之片段，能否拼湊出『全貌』︰

Matrix proof

A spatial rotation is a linear map in one-to-one correspondence with a 3 × 3 rotation matrix $R$ that transforms a coordinate vector $x$ into $X$ , that is $Rx = X$ . Therefore, another version of Euler’s theorem is that for every rotation $R$ , there is a nonzero vector $n$ for which $Rn = n$ ; this is exactly the claim that $n$ is an eigenvector of $R$ associated with the eigenvalue 1. Hence it suffices to prove that 1 is an eigenvalue of $R$ ; the rotation axis of $R$ will be the line $μ n$ , where $n$ is the eigenvector with eigenvalue 1.

A rotation matrix has the fundamental property that its inverse is its transpose, that is

$\displaystyle \mathbf {R} ^{\mathsf {T}}\mathbf {R} =\mathbf {R} \mathbf {R} ^{\mathsf {T}}=\mathbf {I} ,$

where

I

is the 3 × 3 identity matrix and superscript T indicates the transposed matrix.

Compute the determinant of this relation to find that a rotation matrix has determinant ±1. In particular,

$\displaystyle 1=\det(\mathbf {I} )=\det \left(\mathbf {R} ^{\mathsf {T}}\mathbf {R} \right)=\det \left(\mathbf {R} ^{\mathsf {T}}\right)\det(\mathbf {R} )=\det(\mathbf {R} )^{2}\quad \Longrightarrow \quad \det(\mathbf {R} )=\pm 1.$

A rotation matrix with determinant +1 is a proper rotation, and one with a negative determinant −1 is an improper rotation, that is a reflection combined with a proper rotation.

It will now be shown that a rotation matrix $R$ has at least one invariant vector $n$ , i.e., $Rn = n$ . Because this requires that $(R - I) n = 0$ , we see that the vector $n$ must be an eigenvector of the matrix $R$ with eigenvalue $λ = 1$ . Thus, this is equivalent to showing that $det(R - I) = 0$ .

Use the two relations

$\displaystyle \det(-\mathbf {A} )=(-1)^{3}\det(\mathbf {A} )=-\det(\mathbf {A} )\quad$

for any 3 × 3 matrix A and

$\displaystyle \det \left(\mathbf {R} ^{-1}\right)=1\quad$

(since

det(R) = 1

) to compute

$\displaystyle {\begin{aligned}\det(\mathbf {R} -\mathbf {I} )=\det \left((\mathbf {R} -\mathbf {I} )^{\mathsf {T}}\right)&=\det \left(\mathbf {R} ^{\mathsf {T}}-\mathbf {I} \right)=\det \left(\mathbf {R} ^{-1}-\mathbf {R} ^{-1}\mathbf {R} \right)\\&=\det \left(\mathbf {R} ^{-1}(\mathbf {I} -\mathbf {R} )\right)=\det \left(\mathbf {R} ^{-1}\right)\,\det(-(\mathbf {R} -\mathbf {I} ))=-\det(\mathbf {R} -\mathbf {I} )\quad \Longrightarrow \quad \det(\mathbf {R} -\mathbf {I} )=0.\end{aligned}}$

This shows that

λ = 1

is a root (solution) of the characteristic equation, that is,

$\displaystyle \det(\mathbf {R} -\lambda \mathbf {I} )=0\quad {\hbox{for}}\quad \lambda =1.$

In other words, the matrix

R - I

is singular and has a non-zero kernel, that is, there is at least one non-zero vector, say

n

, for which

$\displaystyle (\mathbf {R} -\mathbf {I} )\mathbf {n} =\mathbf {0} \quad \Longleftrightarrow \quad \mathbf {R} \mathbf {n} =\mathbf {n} .$

The line

μ n

for real

μ

is invariant under

R

, i.e.,

μ n

is a rotation axis. This proves Euler’s theorem.

───

Rodrigues’ rotation formula

Statement

If $v$ is a vector in $ℝ 3$ and $k$ is a unit vector describing an axis of rotation about which $v$ rotates by an angle $θ$ according to the right hand rule, the Rodrigues formula is

$\displaystyle \mathbf {v} _{\mathrm {rot} }=\mathbf {v} \cos \theta +(\mathbf {k} \times \mathbf {v} )\sin \theta +\mathbf {k} ~(\mathbf {k} \cdot \mathbf {v} )(1-\cos \theta )\,.$

An alternative statement is to write the axis vector as a cross product $a \times b$ of any two nonzero vectors $a$ and $b$ which define the plane of rotation, and the sense of the angle $θ$ is measured away from $a$ and towards $b$ . Letting $α$ denote the angle between these vectors, the two angles $θ$ and $α$ are not necessarily equal, but they are measured in the same sense. Then the unit axis vector can be written

$\displaystyle \mathbf {k} ={\frac {\mathbf {a} \times \mathbf {b} }{|\mathbf {a} \times \mathbf {b} |}}={\frac {\mathbf {a} \times \mathbf {b} }{|\mathbf {a} ||\mathbf {b} |\sin \alpha }}\,.$

This form may be more useful when two vectors defining a plane are involved. An example in physics is the Thomas precession which includes the rotation given by Rodrigues’ formula, in terms of two non-collinear boost velocities, and the axis of rotation is perpendicular to their plane.

Derivation

Rodrigues’ rotation formula rotates $v$ by an angle $θ$ around vector $k$ by decomposing it into its components parallel and perpendicular to $k$ , and rotating only the perpendicular component.

Let $k$ be a unit vector defining a rotation axis, and let $v$ be any vector to rotate about $k$ by angle $θ$ (right hand rule, anticlockwise in the figure).

Using the dot and cross products, the vector $v$ can be decomposed into components parallel and perpendicular to the axis $k$ ,

$\displaystyle \mathbf {v} =\mathbf {v} _{\parallel }+\mathbf {v} _{\perp }\,,$

where the component parallel to

k

$\displaystyle \mathbf {v} _{\parallel }=(\mathbf {v} \cdot \mathbf {k} )\mathbf {k}$

called the vector projection of

v

k

, and the component perpendicular to

k

$\displaystyle \mathbf {v} _{\perp }=\mathbf {v} -\mathbf {v} _{\parallel }=\mathbf {v} -(\mathbf {k} \cdot \mathbf {v} )\mathbf {k} =-\mathbf {k} \times (\mathbf {k} \times \mathbf {v} )$

called the vector rejection of

v

from

k

The vector $k \times v$ can be viewed as a copy of $v ⊥$ rotated anticlockwise by 90° about $k$ , so their magnitudes are equal but directions are perpendicular. Likewise the vector $k \times (k \times v)$ a copy of $v ⊥$ rotated anticlockwise through $180°$ about $k$ , so that $k \times (k \times v)$ and $v ⊥$ are equal in magnitude but in opposite directions (i.e. they are negatives of each other, hence the minus sign). Expanding the vector triple productestablishes the connection between the parallel and perpendicular components, for reference the formula is $a \times (b \times c) = (a \cdot c) b - (a \cdot b) c$ given any three vectors $a$ , $b$ , $c$ .

The component parallel to the axis will not change magnitude nor direction under the rotation,

$\displaystyle \mathbf {v} _{\parallel \mathrm {rot} }=\mathbf {v} _{\parallel }\,,$

only the perpendicular component will change direction but retain its magnitude, according to

$\displaystyle {\begin{aligned}\left|\mathbf {v} _{\perp \mathrm {rot} }\right|&=\left|\mathbf {v} _{\perp }\right|\,,\\\mathbf {v} _{\perp \mathrm {rot} }&=\cos \theta \mathbf {v} _{\perp }+\sin \theta \mathbf {k} \times \mathbf {v} _{\perp }\,,\end{aligned}}$

and since

k

and

v ∥

are parallel, their cross product is zero

k \times v ∥ = 0

, so that

$\displaystyle \mathbf {k} \times \mathbf {v} _{\perp }=\mathbf {k} \times \left(\mathbf {v} -\mathbf {v} _{\parallel }\right)=\mathbf {k} \times \mathbf {v} -\mathbf {k} \times \mathbf {v} _{\parallel }=\mathbf {k} \times \mathbf {v}$

and it follows

$\displaystyle \mathbf {v} _{\perp \mathrm {rot} }=\cos \theta \mathbf {v} _{\perp }+\sin \theta \mathbf {k} \times \mathbf {v} \,.$

This rotation is correct since the vectors

v ⊥

and

k \times v

have the same length, and

k \times v

v ⊥

rotated anticlockwise through

90°

about

k

. An appropriate scaling of

v ⊥

and

k \times v

using the trigonometric functions sine and cosine gives the rotated perpendicular component. The form of the rotated component is similar to the radial vector in 2D planar polar coordinates

(r, θ)

in the Cartesian basis

$\displaystyle \mathbf {r} =r\cos \theta \mathbf {e} _{x}+r\sin \theta \mathbf {e} _{y}\,,$

where

e x

e y

are unit vectors in their indicated directions.

Now the full rotated vector is

$\displaystyle \mathbf {v} _{\mathrm {rot} }=\mathbf {v} _{\parallel \mathrm {rot} }+\mathbf {v} _{\perp \mathrm {rot} }\,,$

By substituting the definitions of

v ∥rot

and

v ⊥rot

in the equation results in

$\displaystyle {\begin{aligned}\mathbf {v} _{\mathrm {rot} }&=\mathbf {v} _{\parallel }+\cos \theta \,\mathbf {v} _{\perp }+\sin \theta \,\mathbf {k} \times \mathbf {v} \\&=\mathbf {v} _{\parallel }+\cos \theta \left(\mathbf {v} -\mathbf {v} _{\parallel }\right)+\sin \theta \,\mathbf {k} \times \mathbf {v} \\&=\cos \theta \,\mathbf {v} +(1-\cos \theta )\mathbf {v} _{\parallel }+\sin \theta \,\mathbf {k} \times \mathbf {v} \\&=\cos \theta \,\mathbf {v} +(1-\cos \theta )(\mathbf {k} \cdot \mathbf {v} )\mathbf {k} +\sin \theta \,\mathbf {k} \times \mathbf {v} \end{aligned}}$

Vector geometry of Rodrigues’ rotation formula, as well as the decomposition into parallel and perpendicular components.

Matrix notation

Representing $v$ and $k \times v$ as column matrices, the cross product can be expressed as a matrix product

$\displaystyle {\begin{bmatrix}(\mathbf {k} \times \mathbf {v} )_{x}\\(\mathbf {k} \times \mathbf {v} )_{y}\\(\mathbf {k} \times \mathbf {v} )_{z}\end{bmatrix}}={\begin{bmatrix}k_{y}v_{z}-k_{z}v_{y}\\k_{z}v_{x}-k_{x}v_{z}\\k_{x}v_{y}-k_{y}v_{x}\end{bmatrix}}={\begin{bmatrix}0&-k_{z}&k_{y}\\k_{z}&0&-k_{x}\\-k_{y}&k_{x}&0\end{bmatrix}}{\begin{bmatrix}v_{x}\\v_{y}\\v_{z}\end{bmatrix}}\,.$

Letting

K

denote the “cross-product matrix” for the unit vector

k

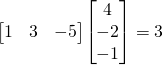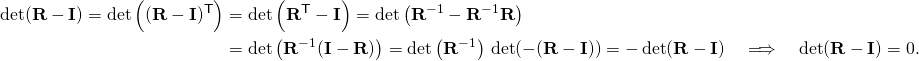
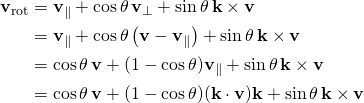
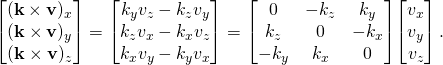
$\displaystyle \mathbf {K} =\left[{\begin{array}{ccc}0&-k_{z}&k_{y}\\k_{z}&0&-k_{x}\\-k_{y}&k_{x}&0\end{array}}\right]\,,$

the matrix equation is, symbolically,

$\displaystyle \mathbf {K} \mathbf {v} =\mathbf {k} \times \mathbf {v}$

for any vector

v

. (In fact,

K

is the unique matrix with this property. It has eigenvalues 0 and

\pm i

Iterating the cross product on the right is equivalent to multiplying by the cross product matrix on the left, in particular

$\displaystyle \mathbf {K} (\mathbf {K} \mathbf {v} )=\mathbf {K} ^{2}\mathbf {v} =\mathbf {k} \times (\mathbf {k} \times \mathbf {v} )\,.$

Moreover, since

k

is a unit vector,

K

has unit 2-norm. The previous rotation formula in matrix language is therefore

$\displaystyle \mathbf {v} _{\mathrm {rot} }=\mathbf {v} +(\sin \theta )\mathbf {K} \mathbf {v} +(1-\cos \theta )\mathbf {K} ^{2}\mathbf {v} \,,\quad \|\mathbf {K} \|_{2}=1\,.$

Note the coefficient of the leading term is now 1, in this notation.

Factorizing the $v$ allows the compact expression

$\begin{aligned}\mathbf {v} _{\mathrm {rot} }&=\mathbf {R} \mathbf {v} \end{aligned}}$

where

$\displaystyle \mathbf {R} =\mathbf {I} +(\sin \theta )\mathbf {K} +(1-\cos \theta )\mathbf {K} ^{2}$

is the rotation matrix through an angle $θ$ anticlockwise about the axis $k$ , and $I$ the 3 × 3 identity matrix. This matrix $R$ is an element of the rotation group $SO(3)$ of $ℝ 3$ , and $K$ is an element of the Lie algebra $so (3)$ generating that Lie group (note that $K$ is skew-symmetric, which characterizes $so (3)$ ). In terms of the matrix exponential,

$\displaystyle \mathbf {R} =\exp(\theta \mathbf {K} )\,.$

To see that the last identity holds, one notes that

$\displaystyle \mathbf {R} (\theta )\mathbf {R} (\phi )=\mathbf {R} (\theta +\phi ),\quad \mathbf {R} (0)=\mathbf {I} \,,$

characteristic of a one-parameter subgroup, i.e. exponential, and that the formulas match for infinitesimal

θ

For an alternative derivation based on this exponential relationship, see exponential map from $so (3)$ to $SO(3)$ . For the inverse mapping, see log map from $SO(3)$ to $so (3)$ .

───

Axis–angle representation

In mathematics, the axis–angle representation of a rotation parameterizes a rotation in a three-dimensional Euclidean space by two quantities: a unit vector $e$ indicating the direction of an axis of rotation, and an angle $θ$ describing the magnitude of the rotation about the axis. Only two numbers, not three, are needed to define the direction of a unit vector $e$ rooted at the origin because the magnitude of $e$ is constrained. For example, the elevation and azimuth angles of $e$ suffice to locate it in any particular Cartesian coordinate frame. The angle $θ$ scalar multiplied by the unit vector $e$ is the axis-angle vector

$\displaystyle {\boldsymbol {\theta }}=\theta \mathbf {e} \,.$

The vector itself does not perform rotations, but is used to construct transformations on vectors that correspond to rotations. The rotation occurs in the sense prescribed by the right-hand rule. The rotation axis is sometimes called theEuler axis.

It is one of many rotation formalisms in three dimensions. The axis–angle representation is predicated on Euler’s rotation theorem, which dictates that any rotation or sequence of rotations of a rigid body in a three-dimensional space is equivalent to a pure rotation about a single fixed axis.

The angle axis vector $θ = θ e$ is a unit vector $e$ multiplied by an angle $θ$ .

Exponential map from ${\mathfrak {so}}$ (3) to SO(3)

The exponential map effects a transformation from the axis-angle representation of rotations to rotation matrices,

$\displaystyle \exp \colon {\mathfrak {so}}(3)\to \mathrm {SO} (3)\,.$

Essentially, by using a Taylor expansion one derives a closed-form relation between these two representations. Given a unit vector

\displaystyle {\mathfrak {so}}

representing the unit rotation axis, and an angle,

θ \in ℝ

, an equivalent rotation matrix

R

is given as follows, where

K

is the cross product matrix of

ω

, that is,

Kv = ω \times v

for all vectors

v \in ℝ 3

$\displaystyle R=\exp(\theta \mathbf {K} )=\sum _{k=0}^{\infty }{\frac {(\theta \mathbf {K} )^{k}}{k!}}=I+\theta \mathbf {K} +{\frac {1}{2!}}(\theta \mathbf {K} )^{2}+{\frac {1}{3!}}(\theta \mathbf {K} )^{3}+\cdots$

Because

K

is skew-symmetric, and the sum of the squares of its above-diagonal entries is 1, the characteristic polynomial

P (t)

K

P (t) = det(K - t I) = -(t 3 + t)

. Since, by the Cayley–Hamilton theorem,

P (K)

= 0, this implies that

$\displaystyle \mathbf {K} ^{3}=-\mathbf {K} \,.$

As a result,

K 4 = - K 2

K 5 = K

K 6 = K 2

K 7 = - K

This cyclic pattern continues indefinitely, and so all higher powers of $K$ can be expressed in terms of $K$ and $K 2$ . Thus, from the above equation, it follows that

$\displaystyle R=I+\left(\theta -{\frac {\theta ^{3}}{3!}}+{\frac {\theta ^{5}}{5!}}-\cdots \right)\mathbf {K} +\left({\frac {\theta ^{2}}{2!}}-{\frac {\theta ^{4}}{4!}}+{\frac {\theta ^{6}}{6!}}-\cdots \right)\mathbf {K} ^{2}\,,$

that is,

$\displaystyle R=I+(\sin \theta )\mathbf {K} +(1-\cos \theta )\mathbf {K} ^{2}\,.$

This is a Lie-algebraic derivation, in contrast to the geometric one in the article Rodrigues’ rotation formula.^[1]

Due to the existence of the above-mentioned exponential map, the unit vector $ω$ representing the rotation axis, and the angle $θ$ are sometimes called the exponential coordinates of the rotation matrix $R$ .

因此我們敢篤定的說︰剛體運動可用『定點』之『平移』與相對『定點』的『轉動』來描述！！

Rigid body

Kinematics

Linear and angular position

The position of a rigid body is the position of all the particles of which it is composed. To simplify the description of this position, we exploit the property that the body is rigid, namely that all its particles maintain the same distance relative to each other. If the body is rigid, it is sufficient to describe the position of at least three non-collinear particles. This makes it possible to reconstruct the position of all the other particles, provided that their time-invariant position relative to the three selected particles is known. However, typically a different, mathematically more convenient, but equivalent approach is used. The position of the whole body is represented by:

the linear position or position of the body, namely the position of one of the particles of the body, specifically chosen as a reference point (typically coinciding with the center of mass or centroid of the body), together with
the angular position (also known as orientation, or attitude) of the body.

Thus, the position of a rigid body has two components: linear and angular, respectively.^[2] The same is true for other kinematic and kinetic quantities describing the motion of a rigid body, such as linear and angular velocity, acceleration, momentum, impulse, andkinetic energy.^[3]

The linear position can be represented by a vector with its tail at an arbitrary reference point in space (the origin of a chosen coordinate system) and its tip at an arbitrary point of interest on the rigid body, typically coinciding with its center of mass or centroid. This reference point may define the origin of a coordinate system fixed to the body.

There are several ways to numerically describe the orientation of a rigid body, including a set of three Euler angles, a quaternion, or a direction cosine matrix (also referred to as a rotation matrix). All these methods actually define the orientation of a basis set (orcoordinate system) which has a fixed orientation relative to the body (i.e. rotates together with the body), relative to another basis set (or coordinate system), from which the motion of the rigid body is observed. For instance, a basis set with fixed orientation relative to an airplane can be defined as a set of three orthogonal unit vectors b₁, b₂, b₃, such that b₁ is parallel to the chord line of the wing and directed forward, b₂ is normal to the plane of symmetry and directed rightward, and b₃ is given by the cross product $\displaystyle b_{3}=b_{1}\times b_{2}$ .

In general, when a rigid body moves, both its position and orientation vary with time. In the kinematic sense, these changes are referred to as translation and rotation, respectively. Indeed, the position of a rigid body can be viewed as a hypothetic translation and rotation (roto-translation) of the body starting from a hypothetic reference position (not necessarily coinciding with a position actually taken by the body during its motion).

Linear and angular velocity

Velocity (also called linear velocity) and angular velocity are measured with respect to a frame of reference.

The linear velocity of a rigid body is a vector quantity, equal to the time rate of change of its linear position. Thus, it is the velocity of a reference point fixed to the body. During purely translational motion (motion with no rotation), all points on a rigid body move with the same velocity. However, when motion involves rotation, the instantaneous velocity of any two points on the body will generally not be the same. Two points of a rotating body will have the same instantaneous velocity only if they happen to lie on an axis parallel to the instantaneous axis of rotation.

Angular velocity is a vector quantity that describes the angular speed at which the orientation of the rigid body is changing and the instantaneous axis about which it is rotating (the existence of this instantaneous axis is guaranteed by the Euler’s rotation theorem). All points on a rigid body experience the same angular velocity at all times. During purely rotational motion, all points on the body change position except for those lying on the instantaneous axis of rotation. The relationship between orientation and angular velocity is not directly analogous to the relationship between position and velocity. Angular velocity is not the time rate of change of orientation, because there is no such concept as an orientation vector that can be differentiated to obtain the angular velocity.

樹莓派、樹莓派之學習、樹莓派之教育

STEM 隨筆︰古典力學︰運動學【二．三】

2018-03-28 懸鉤子

要是我們不熟悉一個程式庫使用的術語︰

ReferenceFrame

class sympy.physics.vector.frame.ReferenceFrame(name, indices=None, latexs=None, variables=None)

A reference frame in classical mechanics.

ReferenceFrame is a class used to represent a reference frame in classical mechanics. It has a standard basis of three unit vectors in the frame’s x, y, and z directions.

It also can have a rotation relative to a parent frame; this rotation is defined by a direction cosine matrix relating this frame’s basis vectors to the parent frame’s basis vectors. It can also have an angular velocity vector, defined in another frame.

……

orient(parent, rot_type, amounts, rot_order=”)

Defines the orientation of this frame relative to a parent frame.

Parameters:	parent : ReferenceFrame The frame that this ReferenceFrame will have its orientation matrix defined in relation to. rot_type : str The type of orientation matrix that is being created. Supported types are ‘Body’, ‘Space’, ‘Quaternion’, ‘Axis’, and ‘DCM’. See examples for correct usage. amounts : list OR value The quantities that the orientation matrix will be defined by. In case of rot_type=’DCM’, value must be a sympy.matrices.MatrixBase object (or subclasses of it). rot_order : str If applicable, the order of a series of rotations.

Parameters:

parent : ReferenceFrame

The frame that this ReferenceFrame will have its orientation matrix defined in relation to.

rot_type : str

The type of orientation matrix that is being created. Supported types are ‘Body’, ‘Space’, ‘Quaternion’, ‘Axis’, and ‘DCM’. See examples for correct usage.

amounts : list OR value

The quantities that the orientation matrix will be defined by. In case of rot_type=’DCM’, value must be a sympy.matrices.MatrixBase object (or subclasses of it).

rot_order : str

If applicable, the order of a series of rotations.

單靠簡單的例子，通常無法弄清用法也︰

Examples

>>> from sympy.physics.vector import ReferenceFrame, Vector
>>> from sympy import symbols, eye, ImmutableMatrix
>>> q0, q1, q2, q3 = symbols('q0 q1 q2 q3')
>>> N = ReferenceFrame('N')
>>> B = ReferenceFrame('B')

Now we have a choice of how to implement the orientation. First is Body. Body orientation takes this reference frame through three successive simple rotations. Acceptable rotation orders are of length 3, expressed in XYZ or 123, and cannot have a rotation about about an axis twice in a row.

>>> B.orient(N, 'Body', [q1, q2, q3], '123')
>>> B.orient(N, 'Body', [q1, q2, 0], 'ZXZ')
>>> B.orient(N, 'Body', [0, 0, 0], 'XYX')

Next is Space. Space is like Body, but the rotations are applied in the opposite order.

>>> B.orient(N, 'Space', [q1, q2, q3], '312')

Next is Quaternion. This orients the new ReferenceFrame with Quaternions, defined as a finite rotation about lambda, a unit vector, by some amount theta. This orientation is described by four parameters: q0 = cos(theta/2) q1 = lambda_x sin(theta/2) q2 = lambda_y sin(theta/2) q3 = lambda_z sin(theta/2) Quaternion does not take in a rotation order.

>>> B.orient(N, 'Quaternion', [q0, q1, q2, q3])

Next is Axis. This is a rotation about an arbitrary, non-time-varying axis by some angle. The axis is supplied as a Vector. This is how simple rotations are defined.

>>> B.orient(N, 'Axis', [q1, N.x + 2 * N.y])

Last is DCM (Direction Cosine Matrix). This is a rotation matrix given manually.

>>> B.orient(N, 'DCM', eye(3))
>>> B.orient(N, 'DCM', ImmutableMatrix([[0, 1, 0], [0, 0, -1], [-1, 0, 0]]))

比方說『Body』和『Space』都可指『歐拉角』，讀一讀維基百科詞條或能明白所指是什麼︰

歐拉角

萊昂哈德·歐拉用歐拉角來描述剛體在三維歐幾里得空間的取向。對於任何參考系，一個剛體的取向，是依照順序，從這參考系，做三個歐拉角的旋轉而設定的。所以，剛體的取向可以用三個基本旋轉矩陣來決定。換句話說，任何關於剛體旋轉的旋轉矩陣是由三個基本旋轉矩陣複合而成的。

三個歐拉角： ( $α, β, γ$ )。藍色的軸是 xyz-軸，紅色的軸是 XYZ-坐標軸。綠色的線是交點線 (N)。

靜態的定義

對於在三維空間裏的一個參考系，任何坐標系的取向，都可以用三個歐拉角來表現。參考系又稱為實驗室參考系，是靜止不動的。而坐標系則固定於剛體，隨著剛體的旋轉而旋轉。

參閲右圖。設定xyz-軸為參考系的參考軸。稱 xy-平面與 XY-平面的相交為交點線，用英文字母（N）代表。 zxz 順規的歐拉角可以靜態地這樣定義：

$α$ 是x-軸與交點線的夾角，
$β$ 是z-軸與Z-軸的夾角，
$γ$ 是交點線與X-軸的夾角。

很可惜地，對於夾角的順序和標記，夾角的兩個軸的指定，並沒有任何常規。科學家對此從未達成共識。每當用到歐拉角時，我們必須明確的表示出夾角的順序，指定其參考軸。

實際上，有許多方法可以設定兩個坐標系的相對取向。歐拉角方法只是其中的一種。此外，不同的作者會用不同組合的歐拉角來描述，或用不同的名字表示同樣的歐拉角。因此，使用歐拉角前，必須先做好明確的定義。

角值範圍

$α$ 、 $γ$ 值分別從 0 至 $2π$ 弧度。
$β$ 值從 0 至 $π$ 弧度。

對應於每一個取向，設定的一組歐拉角都是獨特唯一的；除了某些例外：

兩組歐拉角的 $α$ ，一個是0，一個是 $2π$ ，而 $β$ 與 $γ$ 分別相等，則此兩組歐拉角都描述同樣的取向。

兩組歐拉角的 $γ$ ，一個是 0，一個是 $2π$ ，而 $α$ 與 $β$ 分別相等，則此兩組歐拉角都描述同樣的取向。

旋轉矩陣

前面提到，設定剛體取向的旋轉矩陣 $\displaystyle [\mathbf {R} ]$ 是由三個基本旋轉矩陣合成的：

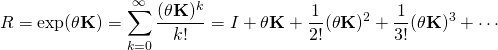
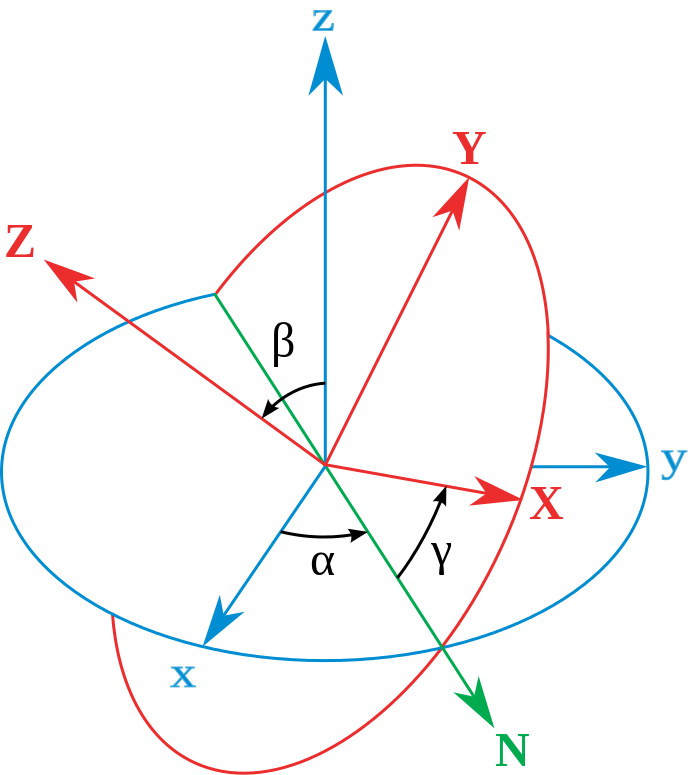
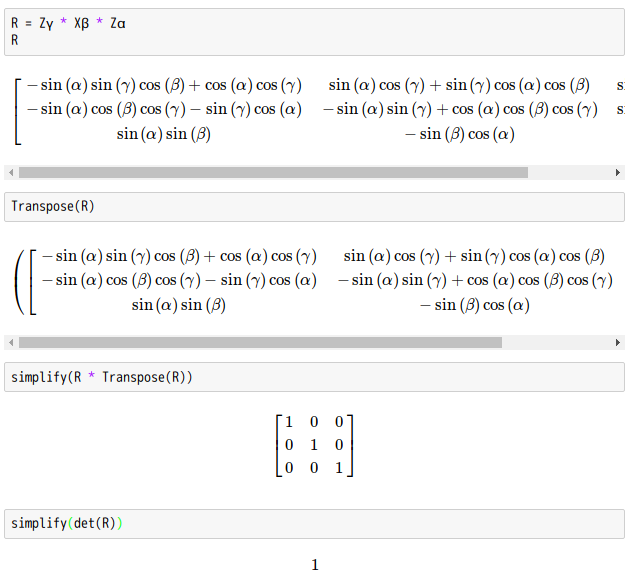
$\displaystyle [\mathbf {R} ]={\begin{bmatrix}\cos \gamma &\sin \gamma &0\\-\sin \gamma &\cos \gamma &0\\0&0&1\end{bmatrix}}{\begin{bmatrix}1&0&0\\0&\cos \beta &\sin \beta \\0&-\sin \beta &\cos \beta \end{bmatrix}}{\begin{bmatrix}\cos \alpha &\sin \alpha &0\\-\sin \alpha &\cos \alpha &0\\0&0&1\end{bmatrix}}$

從左到右依次代表繞著z軸的旋轉、繞著交點線的旋轉、繞著Z軸的旋轉。

經過一番運算,

$\displaystyle [\mathbf {R} ]={\begin{bmatrix}\cos \alpha \cos \gamma -\cos \beta \sin \alpha \sin \gamma &\sin \alpha \cos \gamma +\cos \beta \cos \alpha \sin \gamma &\sin \beta \sin \gamma \\-\cos \alpha \sin \gamma -\cos \beta \sin \alpha \cos \gamma &-\sin \alpha \sin \gamma +\cos \beta \cos \alpha \cos \gamma &\sin \beta \cos \gamma \\\sin \beta \sin \alpha &-\sin \beta \cos \alpha &\cos \beta \end{bmatrix}}$

\displaystyle [\mathbf {R} ]

的逆矩陣是：

$\displaystyle [\mathbf {R} ]^{-1}={\begin{bmatrix}\cos \alpha \cos \gamma -\cos \beta \sin \alpha \sin \gamma &-\cos \alpha \sin \gamma -\cos \beta \sin \alpha \cos \gamma &\sin \beta \sin \alpha \\\sin \alpha \cos \gamma +\cos \beta \cos \alpha \sin \gamma &-\sin \alpha \sin \gamma +\cos \beta \cos \alpha \cos \gamma &-\sin \beta \cos \alpha \\\sin \beta \sin \gamma &\sin \beta \cos \gamma &\cos \beta \end{bmatrix}}$

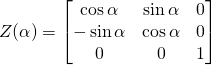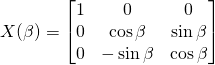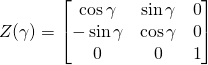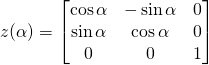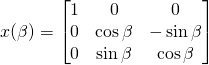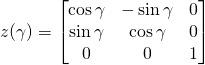別種順序

在古典力學裏，時常用 zxz 順規來設定歐拉角；照著第二個轉動軸的軸名，簡稱為 x 順規。另外，還有別種歐拉角組。合法的歐拉角組中，唯一的限制是，任何兩個連續的旋轉，必須繞著不同的轉動軸旋轉。因此，一共有12種順規。例如， y 順規，第二個轉動軸是 y-軸，時常用在量子力學、核子物理學、粒子物理學。另外，還有一種順規， xyz 順規，是用在航空航天工程學；參閱泰特-布萊恩角。

動態的定義

我們也可以給予歐拉角兩種不同的動態定義。一種是繞著固定於剛體的坐標軸的三個旋轉的複合；另外一種是繞著實驗室參考軸的三個旋轉的複合。用動態的定義，我們能更了解，歐拉角在物理上的含義與應用。特別注意，以下的描述, XYZ 坐標軸是旋轉的剛體坐標軸；而 xyz 坐標軸是靜止不動的實驗室參考軸。

A) 繞著 XYZ 坐標軸旋轉：最初，兩個坐標系統 xyz 與 XYZ 的坐標軸都是重疊著的。開始先繞著Z-軸旋轉 $α$ 角值。然後，繞著 X-軸旋轉 $β$ 角值。最後，繞著 Z-軸作角值 $γ$ 的旋轉。

B) 繞著 xyz 坐標軸旋轉：最初，兩個坐標系統 xyz 與 XYZ 的坐標軸都是重疊著的。開始先繞著z-軸旋轉 $γ$ 角值。然後，繞著 x-軸旋轉 $β$ 角值。最後，繞著 z-軸作角值 $α$ 的旋轉。

參閱歐拉角圖，定義A與靜態定義的相等，這可以直接用幾何製圖方法來核對。

定義A與定義B的相等可以用旋轉矩陣來證明：

思考任何一點 $\displaystyle P_{1}\,$ ，在 xy z與 XYZ坐標系統的坐標分別為 $\displaystyle \mathbf {r} _{1}\,$ 與 $\displaystyle \mathbf {R} _{1}\,$ 。定義角算符 $\displaystyle Z(\alpha )\,$ 為繞著Z-軸旋轉 $α$ 角值。那麼，定義 A 可以表述如下：

$\displaystyle \mathbf {R} _{1}=Z(\gamma )\circ X(\beta )\circ Z(\alpha )\circ \mathbf {r} _{1}\,$ 。

用旋轉矩陣表示,

$\displaystyle Z(\alpha )={\begin{bmatrix}\cos \alpha &\sin \alpha &0\\-\sin \alpha &\cos \alpha &0\\0&0&1\end{bmatrix}}\,$ ，

$\displaystyle X(\beta )={\begin{bmatrix}1&0&0\\0&\cos \beta &\sin \beta \\0&-\sin \beta &\cos \beta \end{bmatrix}}\,$ ，

$\displaystyle Z(\gamma )={\begin{bmatrix}\cos \gamma &\sin \gamma &0\\-\sin \gamma &\cos \gamma &0\\0&0&1\end{bmatrix}}\,$ 。

思考任何一點 $\displaystyle P_{2}\,$ ，在 xyz 與 XYZ 坐標系統的坐標分別為 $\displaystyle \mathbf {r} _{2}\,$ 與 $\displaystyle \mathbf {R} _{2}\,$ 。定義角算符 $\displaystyle z(\alpha )\,$ 為繞著z-軸旋轉 $α$ 角值。則定義 B 可以表述如下：

$\displaystyle \mathbf {r} _{2}=z(\alpha )\circ x(\beta )\circ z(\gamma )\circ \mathbf {R} _{2}\,$ 。

用旋轉矩陣表示,

$\displaystyle z(\alpha )={\begin{bmatrix}\cos \alpha &-\sin \alpha &0\\\sin \alpha &\cos \alpha &0\\0&0&1\end{bmatrix}}\,$ ，

$\displaystyle x(\beta )={\begin{bmatrix}1&0&0\\0&\cos \beta &-\sin \beta \\0&\sin \beta &\cos \beta \end{bmatrix}}\,$ ，

$\displaystyle z(\gamma )={\begin{bmatrix}\cos \gamma &-\sin \gamma &0\\\sin \gamma &\cos \gamma &0\\0&0&1\end{bmatrix}}\,$ 。

假設， $\displaystyle \mathbf {r} _{1}=\mathbf {r} _{2}\,$ 那麼，

$\displaystyle \mathbf {r} _{1}=z(\alpha )\circ x(\beta )\circ z(\gamma )\circ \mathbf {R} _{2}\,$ 。

乘以逆算符，

$\displaystyle z^{-1}(\gamma )\circ x^{-1}(\beta )\circ z^{-1}(\alpha )\circ \mathbf {r} _{1}=z^{-1}(\gamma )\circ x^{-1}(\beta )\circ z^{-1}(\alpha )\circ z(\alpha )\circ x(\beta )\circ z(\gamma )\circ \mathbf {R} _{2}\,$ 。