假使說給定了一個『 λ表達式』 ![]() ,有人『第一步』這樣作『
,有人『第一步』這樣作『 ![]() 化約』︰
化約』︰
![]()
,也有人『第一步』這樣作『 ![]() 化約』︰
化約』︰
![]()
,這樣不同的『步驟選擇』是否會產生『不同結果』的呢?如果說再次繼續進行『 ![]() 化約』,兩者都會得到︰
化約』,兩者都會得到︰
![]()
,於是我們就可以歸結的說『 ![]() 化約』不管是用著怎麽樣的『步驟次序』,都一定能夠得到『相同結果』的嗎??
化約』不管是用著怎麽樣的『步驟次序』,都一定能夠得到『相同結果』的嗎??
為了考察不同次序步驟的『化約策略』,首先讓我們定義『單步 ![]() 化約』︰
化約』︰
![]()
是指表達式 ![]() 是經由表達式
是經由表達式 ![]() 中的某一函式應用子表達式
中的某一函式應用子表達式 ![]() 『
『 ![]() 化約』而得來。假使『約定』零步
化約』而得來。假使『約定』零步 ![]() 化約是說 『
化約是說 『![]() 』,這樣我們就可以說『單步』或『多次單步』之『單步
』,這樣我們就可以說『單步』或『多次單步』之『單步 ![]() 化約』的『化約封閉性』︰
化約』的『化約封閉性』︰
![]()
,是講存在一個『單步 ![]() 化約』的『序列』
化約』的『序列』
![]()
。某一表達式 ![]() 我們稱它是『
我們稱它是『 ![]() 可化約』
可化約』![]() -redex 是指這個表達式還有『未化約』的子應用表達式
-redex 是指這個表達式還有『未化約』的子應用表達式 ![]() 。如果經過『有限的』化約序列,最終抵達一個『沒有未化約』的表達式
。如果經過『有限的』化約序列,最終抵達一個『沒有未化約』的表達式 ![]() ,也就是說
,也就是說 ![]() 中沒有
中沒有 ![]() -redex,這時我們將
-redex,這時我們將 ![]() 稱之為『
稱之為『 ![]() 正規元型』normal form。於是我們就可以問︰
正規元型』normal form。於是我們就可以問︰
各種不同的『化約序列』如果存在『 ![]() 正規元型』,那它們是相同的嗎?
正規元型』,那它們是相同的嗎?
【Church-Rosser 定理】說
如果 ![]() 而且
而且 ![]() ;那麼就會存在一個
;那麼就會存在一個 ![]() , 使得
, 使得 ![]() 以及
以及 ![]() 。
。
所以可以講不同的『化約序列』之『 ![]() 正規元型』,除了其內函式中的『受約束變元』之『虛名』不同外 ── 可以作『
正規元型』,除了其內函式中的『受約束變元』之『虛名』不同外 ── 可以作『 ![]() 變換』使之一樣 ──,都是『相同的』。這是一個非常重要的歸結,設想萬一它不是這樣,那所謂的『計算』不就成『笑話』了嗎!然而需要小心的是『
變換』使之一樣 ──,都是『相同的』。這是一個非常重要的歸結,設想萬一它不是這樣,那所謂的『計算』不就成『笑話』了嗎!然而需要小心的是『 ![]() 化約』是『單行道』,也就是說
化約』是『單行道』,也就是說 ![]() 成立,並不代表
成立,並不代表 ![]() 正確。比方講
正確。比方講 ![]() ,從結果變元
,從結果變元 ![]() 又要怎麼得回原來函式應用的呢?
又要怎麼得回原來函式應用的呢?
那麼『 ![]() 化約策略』Reduction Strategy 又是什麼呢?它是一個『函式』
化約策略』Reduction Strategy 又是什麼呢?它是一個『函式』![]() ,可以定義如下︰
,可以定義如下︰
一、『定義域』與『對應域』是『所有的 λ 表達式』構成的集合
二、如果 ![]() 是一個『
是一個『 ![]() 正規元型』,
正規元型』,![]()
三、假使 ![]() 不是『
不是『 ![]() 正規元型』,化約策略會依據特定方式選擇
正規元型』,化約策略會依據特定方式選擇 ![]() 中的某一『優先』
中的某一『優先』 ![]() -redex 子表達項
-redex 子表達項 ![]() ,
,![]()
這樣看來 ![]() 函式選擇了特定的『步驟次序』── 策略 ── 來作『單步
函式選擇了特定的『步驟次序』── 策略 ── 來作『單步 ![]() 化約』,這也是『程式』之『最佳化』optimize 的源起。然而不是每種『化約策略』都能夠抵達存在的『
化約』,這也是『程式』之『最佳化』optimize 的源起。然而不是每種『化約策略』都能夠抵達存在的『 ![]() 正規元型』。舉例說兩種簡單的『左』和『右』化約策略,它總是優先選擇表達式中的『最左』與『最右』
正規元型』。舉例說兩種簡單的『左』和『右』化約策略,它總是優先選擇表達式中的『最左』與『最右』 ![]() -redex 子表達項 。
-redex 子表達項 。
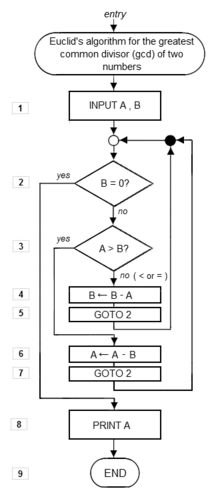
用『左』策略會得到『上圖』,用『右』策略會卡在 ![]() 。
。
所謂的『正規策略』是說用這個策略能夠得到『所有可能存在的』 ![]() 正規元型。事實上從邏輯推理可以證明『最左優先』策略是一種『正則策略』,果真是『天左旋』的乎!!
正規元型。事實上從邏輯推理可以證明『最左優先』策略是一種『正則策略』,果真是『天左旋』的乎!!
最後讓我們談談『相等』的概念以及『等號 ![]() 』的使用,相等和『邏輯推導規則』有關︰
』的使用,相等和『邏輯推導規則』有關︰
一、 ![]() ,無條件自反律
,無條件自反律
二、 ![]() ,對稱律
,對稱律
三、 ![]() ,遷移律
,遷移律
此處的 ![]() 是講,如果由『前提』Premises,我們可以邏輯上推導出『結論』Conclusion。也就是說這是廣義的『相等』關係的『內涵』。
是講,如果由『前提』Premises,我們可以邏輯上推導出『結論』Conclusion。也就是說這是廣義的『相等』關係的『內涵』。
此處雖然並不定義『 λ 運算』中所謂的『等式』到底是指什麼?只是從『基元』觀點下,就是說假設我們基本『知道』或者『同意』兩個表達式『![]() 』所指的意義── 比方說指相同的計算結果 ──,於是我們可以提出下面的『 λ 理論』︰
』所指的意義── 比方說指相同的計算結果 ──,於是我們可以提出下面的『 λ 理論』︰
一、 ![]() ,『應用』於『等式』之『結果』相等
,『應用』於『等式』之『結果』相等
二、 ![]() ,『等式』之『函式』的『應用』相等
,『等式』之『函式』的『應用』相等
三、 ![]() ,『等式』之『函式抽象』相等
,『等式』之『函式抽象』相等
四、 ![]() ,『應用』是無條件的『化約相等』
,『應用』是無條件的『化約相等』
五、 ![]() 擴張,
擴張, ![]() ,『外延』相同的『函式』相等
,『外延』相同的『函式』相等
簡單的將『變元』、『函式』和『應用』結構起來形成的『 λ 運算』,彷彿是『概念』的『水滴』墜落『心湖』,激起『思想』的『浪花』。這些『浪花』彼此『碰撞』,掀起陣陣『漣漪』,最後『波光』點點,早就分不清哪兒是『始點』,哪兒又是『終點』!!
─── 《Λ 運算︰概念導引《四》》
知道 ![]() 是什麼。且能將之聯繫上 PLT
是什麼。且能將之聯繫上 PLT
Programming language theory
Programming language theory (PLT) is a branch of computer science that deals with the design, implementation, analysis, characterization, and classification of programming languages and their individual features. It falls within the discipline of computer science, both depending on and affecting mathematics, software engineering, linguistics and even cognitive science. It is a well-recognized branch of computer science, and an active research area, with results published in numerous journals dedicated to PLT, as well as in general computer science and engineering publications.
History
In some ways, the history of programming language theory predates even the development of programming languages themselves. The lambda calculus, developed by Alonzo Church and Stephen Cole Kleene in the 1930s, is considered by some to be the world’s first programming language, even though it was intended to model computation rather than being a means for programmers to describe algorithms to a computer system. Many modern functional programming languages have been described as providing a “thin veneer” over the lambda calculus,[1] and many are easily described in terms of it.
The first programming language to be invented was Plankalkül, which was designed by Konrad Zuse in the 1940s, but not publicly known until 1972 (and not implemented until 1998). The first widely known and successful high-level programming language was Fortran, developed from 1954 to 1957 by a team of IBM researchers led by John Backus. The success of FORTRAN led to the formation of a committee of scientists to develop a “universal” computer language; the result of their effort was ALGOL 58. Separately, John McCarthy of MIT developed the Lisp programming language (based on the lambda calculus), the first language with origins in academia to be successful. With the success of these initial efforts, programming languages became an active topic of research in the 1960s and beyond.
大體明白 PLT Redex 名目也︰
PLT Redex is a domain-specific language designed for specifying and debugging operational semantics. Write down a grammar and the reduction rules, and PLT Redex allows you to interactively explore terms and to use randomized test generation to attempt to falsify properties of your semantics.
PLT Redex is embedded in Racket, meaning all of the convenience of a modern programming language is available, including standard libraries (and non-standard ones) and a program-development environment.
Getting started: Install Racket, and try the tutorial.
Book: Semantics Engineering with PLT Redex (SEwPR) by Matthias Felleisen,Robert Bruce Findler, and Matthew Flatt gives the mathematical background for operational semantics, as well as a tutorial introduction to Redex. The preface, table of contents, and an example syllabus are available online. The book is available fromMIT Press.
Documentation: The reference manual contains all of the gory details of all of Redex’s operators.
Citation: If you use a reduction semantics and/or you modeled a reduction semantics with Redex and you wish to give academic credit, please cite the book (above). If you are studying the effectiveness of meta-tools, the proper citation is our POPL 2012 paper.
至於那個
![]() v.7.2
v.7.2
2 Long Tutorial
This tutorial is derived from a week-long Redex summer school, run July 27–31, 2015 at the University of Utah.
2.1 The Theoretical Framework
| Goals |
| — |
| — |
| — |
| — |
| — |
| — |
| — |
The lambda calculus:
e = x | (\x.e) | (e e)
Terms vs trees, abstract over concrete syntax
Encode some forms of primitives: numbers, booleans – good for theory of computation; mostly irrelevant for PL. extensions with primitive data
e = x | (\x.e) | (e e) | tt | ff | (if e e e)
What we want: develop LC as a model of a PL. Because of history, this means two things: a simple logic for calculating with the terms of the language e == e’ and a system for determining the value of a program. The former is the calculus, the latter is thesemantics.
Both start with basic notions of reduction (axioms). They are just relation on terms:
((\x.e) e’) beta e[x=e’]
((\x.e) e’) beta [e’/x]e
Think substitution via tree surgery, preserving bindings
Here are two more, often done via external interpretation functions (δ)
(if tt e e’) if-tt e
(if ff e e’) if-ff e’
If this is supposed to be a theory of functions (and if expressions) we need to be able to use this relations in context
| e xyz e’ |
| ————– |
| e = e’ |
| e = e’ e = e’ e = e’ |
| ————– ————– ————– |
| e e” = e’ e” e” e = e” e’ \x.e = \x.e’ |
| plus reflexivity, symmetry, and transitivity |
Now you have an equational system. what’s it good for? you can prove such facts as
e (Y e) = (Y e)
meaning every single term has a fixpoint
All of the above is mathematics but it is just that, mathematics. It might be considered theory of computation, but it is not theory of programming languages. But we can use these ideas to create a theory of programming languages. Plotkin’s 1974 TCS paper on call-by-name versus call-by-value shows how to create a theory of programming languages.
In addition, Plotkin’s paper also sketches several research programs, mostly on scaling up his ideas to the full spectrum of languages but also on the precise connection between by-value and by-name their relationship, both at the proof-theoretical level as well as at the model-theoretic level.
- Start from an abstract syntax, plus notions of scope and scope-preserving substitution. Consider closed terms Programs.
- Identify a subset of expressions as Values. Use v to range over Values.Note The complement of this set was (later) dubbed computations, due to Moggi’s work under Plotkin.
- Define basic notions of reduction (axioms). Examples:
((\x.e) e’) beta-name e[x=e’]
((\x.e) v) beta-value e[x=v]
- Inductively generate an equational theory from the basic notions of reduction.
- This theory defines a semantics, that is, a relation eval from programs to values:
eval : Program x Value
def e eval v iff e = v
- Prove that eval is a function, and you have got yourself a specification of an interpreter.
eval : Program -> Value
eval(e) = v
Note This step often reuses a variant of the Church-Rosser theorem of the mathematical theory of lambda calculus.
- Prove that the calculus satisfies a Curry-Feys standard reduction property. This gives you a second semantics:
eval-standard : Program -> Value
def eval-standard(e) = v iff e standard reduces to v
The new semantics is correct:Theorem eval-standard = eval
Standard reduction is a strategy for the lambda calculus, that is, a function that picks the next reducible expression (called redex) to reduce. Plotkin specifically uses the leftmost-outermost strategy but others may work, too.
- The interpreter of a programming language (non-constructively) generates a theory of equivalence on phrases.
def e ~ e’ iff placing e and e’ into any context yields programs that produce the same observable behavior according to eval
Theorem ~ is the coarsest equivalence theory and thus unique.
- Theorem e = e’ implies e ~ e’. Naturally the reverse doesn’t hold.
- Plotkin’s “algorithm” applies to imperative programming language, especially those extending the lambda calculus syntax with (variable) assignment and non-local control operators.Imperative Extensions explains how two of these work.
- It is possible to derive useful abstract register machines from the standard reduction semantics of the programming language
Each machine M defines a new semantics:
def eval-M(e) = v iff load M with e, run, unload, yields v
For each of these functions, we can prove an equivalence theorem.
Theorem eval-M = eval-standard = eval
未曾深研,不敢亂講呦。








 cd lambda-py/base/
rock64@rock64:~/lambda-py/base
cd lambda-py/base/
rock64@rock64:~/lambda-py/base![Rendered by QuickLaTeX.com python3 Python 3.5.3 (default, Sep 27 2018, 17:25:39) [GCC 6.3.0 20170516] on linux Type "help", "copyright", "credits" or "license" for more information. >>> ... Ellipsis >>> l = [] >>> l.append(l) >>> print(l) [[...]] >>></pre> <span style="color: #666699;">果說此意乎??</span> <h1><span style="color: #ff9900;"><a style="color: #ff9900;" href="https://mail.python.org/pipermail/tutor/2017-August/111817.html">[Tutor] What exactly does the three dots do? Why such as thing?</a></span></h1> <span style="color: #808080;"><b>Steven D'Aprano</b> <a style="color: #808080;" title="[Tutor] What exactly does the three dots do? Why such as thing?" href="mailto:tutor%40python.org?Subject=Re%3A%20%5BTutor%5D%20What%20exactly%20does%20the%20three%20dots%20do%3F%20Why%20such%20as%20thing%3F&In-Reply-To=%3C20170810124759.GC7395%40ando.pearwood.info%3E">steve at pearwood.info </a></span> <span style="color: #808080;"> <i>Thu Aug 10 08:47:59 EDT 2017</i></span> <span style="color: #808080;">On Wed, Aug 09, 2017 at 12:06:37PM -0400, C W wrote:</span> <span style="color: #808080;">> Dear Python experts,</span> <span style="color: #808080;">> </span> <span style="color: #808080;">> What exactly does the three dots do?</span> <span style="color: #808080;">> > aList = ...</span> <span style="color: #808080;">... is literal syntax for the Ellipsis singleton object.</span> <span style="color: #808080;">Ellipsis was added to the language at the express request of the numpy </span><span style="color: #808080;">developers. Although numpy is a third-party project outside of the </span><span style="color: #808080;">standard library, it is big enough and important enough that their </span><span style="color: #808080;">requests carry a LOT of weight with the core Python devs. Other features </span><span style="color: #808080;">Python has that were originally added at the request of numpy include:</span> <span style="color: #808080;">- extended slicing with two colons obj[a:b:c]</span> <span style="color: #808080;">- the @ operator used by numpy for matrix multiplication.</span> <span style="color: #808080;">I don't know what Ellipsis is used for by numpy, but now it makes a </span> <span style="color: #808080;">convenient pseudo-pass command:</span> <span style="color: #808080;">class X:</span> <span style="color: #808080;"> ...</span> <span style="color: #808080;">def func():</span> <span style="color: #808080;"> ...</span> <span style="color: #808080;">> It's an ellipsis, a spot holder to later. But what data type is it: vector,</span> <span style="color: #808080;">> matrix?</span> <span style="color: #808080;">Its a singleton object. Think of it as a sibling to None and </span> <span style="color: #808080;">NotImplemented, but with optional funny syntactic sugar ... to refer to </span><span style="color: #808080;">it.</span> <span style="color: #808080;">None is a special value used as "no such value", or nil or null;</span> <span style="color: #808080;">NotImplemented is a special value used by operator dunder methods like </span><span style="color: #808080;">__add__ and __mul__ to mean "I can't handle this argument";</span> <span style="color: #808080;">Ellipsis is a special value used by numpy to mean whatever it is that </span> <span style="color: #808080;">numpy uses it to me.</span> <span style="color: #808080;">-- </span> <span style="color: #808080;">Steve</span> <span style="color: #666699;">心懷疑問?!</span> <pre class="lang:default decode:true ">rock64@rock64:~](http://www.freesandal.org/wp-content/ql-cache/quicklatex.com-bd9460b4c2ad61852d63ff7ace3955a5_l3.png) python3
Python 3.5.3 (default, Sep 27 2018, 17:25:39)
[GCC 6.3.0 20170516] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> 無限大 = int('inf')
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: invalid literal for int() with base 10: 'inf'
>>> 無限大 = float('inf')
>>> 無限大 == 無限大
True
>>> 無限大 * 0
nan
>>> nan = int('nan')
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: invalid literal for int() with base 10: 'nan'
>>> nan = float('nan')
>>> nan == nan
False
>>> nan * 0
nan
>>> nan / nan
nan
>>> ... == nan
False
>>> ... == 無限大
False
>>>
python3
Python 3.5.3 (default, Sep 27 2018, 17:25:39)
[GCC 6.3.0 20170516] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>> 無限大 = int('inf')
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: invalid literal for int() with base 10: 'inf'
>>> 無限大 = float('inf')
>>> 無限大 == 無限大
True
>>> 無限大 * 0
nan
>>> nan = int('nan')
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
ValueError: invalid literal for int() with base 10: 'nan'
>>> nan = float('nan')
>>> nan == nan
False
>>> nan * 0
nan
>>> nan / nan
nan
>>> ... == nan
False
>>> ... == 無限大
False
>>>
 v.7.2
v.7.2
_2-1.png)
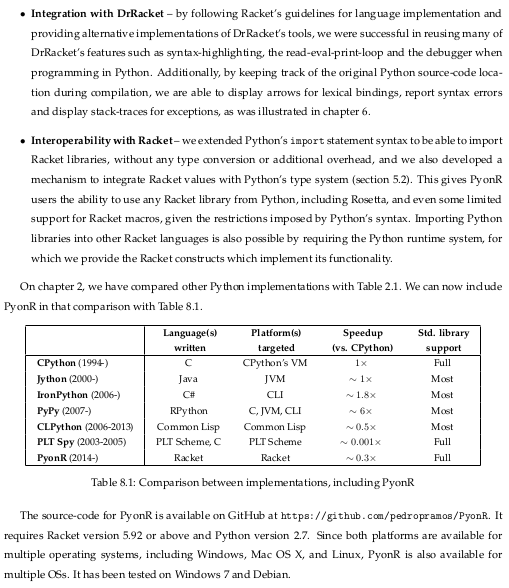
![Rendered by QuickLaTeX.com python Python 2.7.13 (default, Sep 26 2018, 18:42:22) [GCC 6.3.0 20170516] on linux2 Type "help", "copyright", "credits" or "license" for more information. >>> l = [] >>> l.append(l) >>> print l [[...]] >>></pre> <span style="color: #666699;">那麼是否是 <a style="color: #666699;" href="https://beautifulracket.com/appendix/glossary.html#source-to-source-compiler">source-to-source compiler</a></span> <span style="color: #808080;"><strong>source-to-source compiler</strong> A <a class="glossary" style="color: #808080;" href="https://beautifulracket.com/appendix/glossary.html#compiler"><span class="glossary-link-text">compiler</span></a> that converts the <a class="glossary" style="color: #808080;" href="https://beautifulracket.com/appendix/glossary.html#source-code"><span class="glossary-link-text">source code</span></a> of one language into the source code of another. All Racket-implemented languages are essentially source-to-source compilers from the source language to Racket. Also called a <a class="glossary" style="color: #808080;" href="https://beautifulracket.com/appendix/glossary.html#transcompiler"><span class="glossary-link-text">transcompiler</span></a>.</span> <span style="color: #808080;">※ 註︰</span> <img class="alignnone size-full wp-image-97045" src="http://www.freesandal.org/wp-content/uploads/PyonR_1-1.png" alt="" width="515" height="370" /> <span style="color: #666699;">有所侷限呢?</span> <span style="color: #666699;">對比著 <a style="color: #666699;" href="https://github.com/brownplt/lambda-py">lambda-py</a> 的結果︰</span> <pre class="lang:default decode:true ">rock64@rock64:~](http://www.freesandal.org/wp-content/ql-cache/quicklatex.com-a98aa17c1cc99dd66c5de2f339c7671b_l3.png) cd lambda-py/base/
rock64@rock64:~/lambda-py/base
cd lambda-py/base/
rock64@rock64:~/lambda-py/base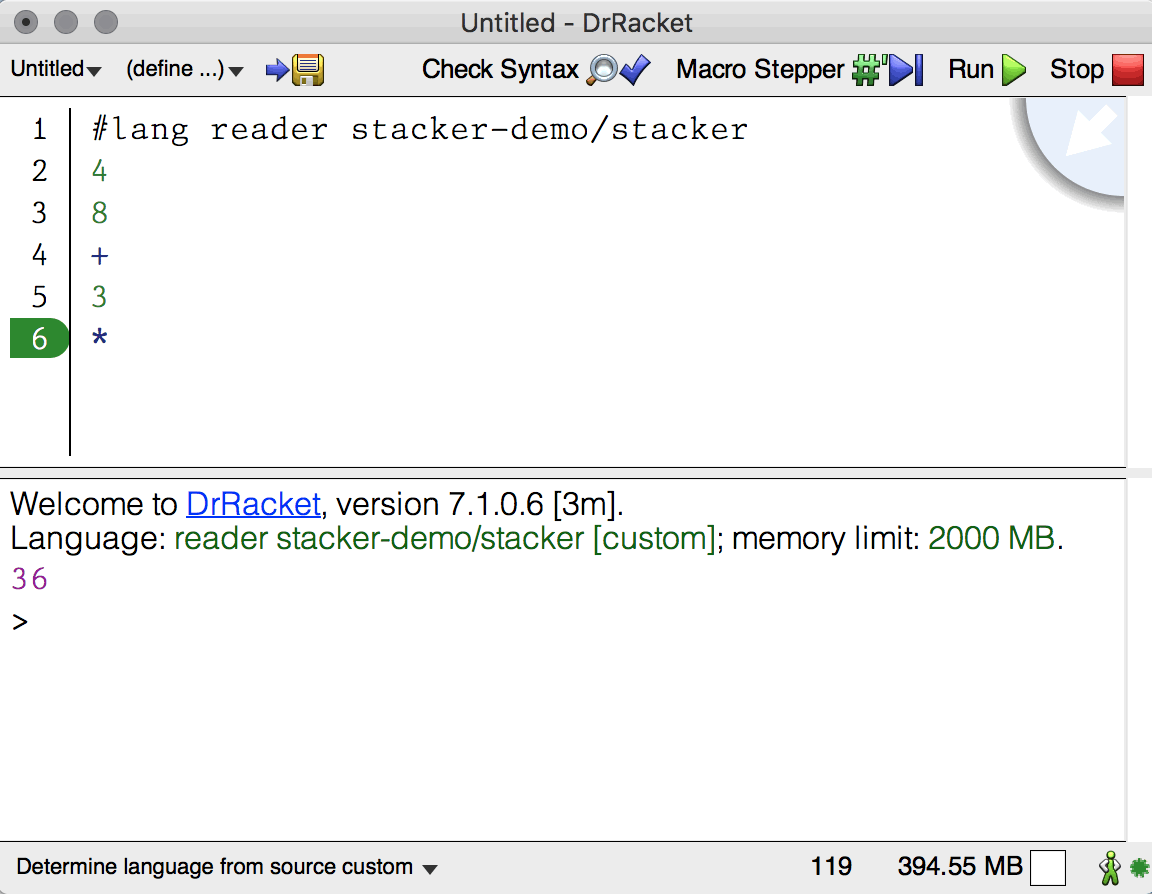
_1-1.png)

_5.png)


_2.png)