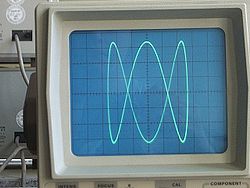
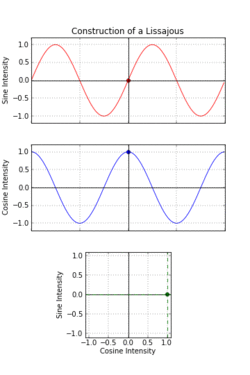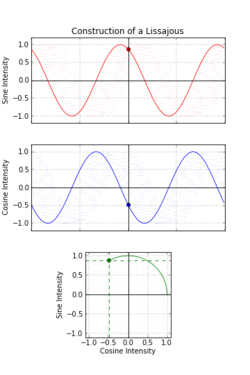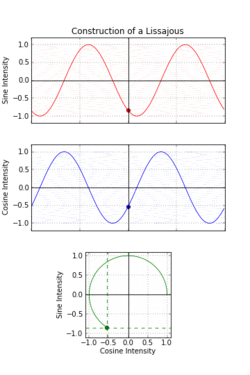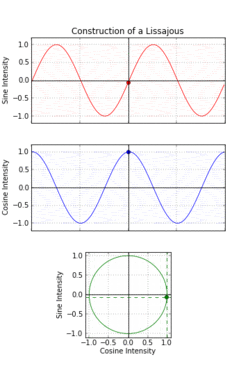
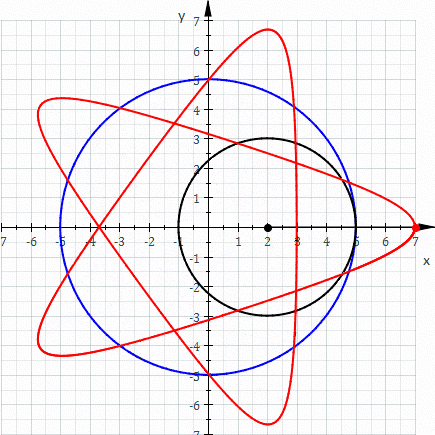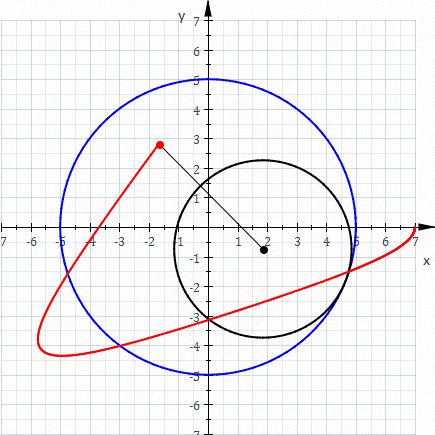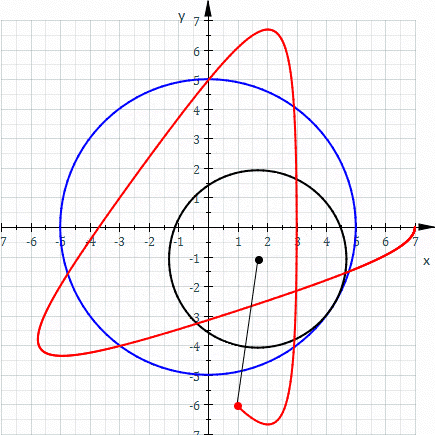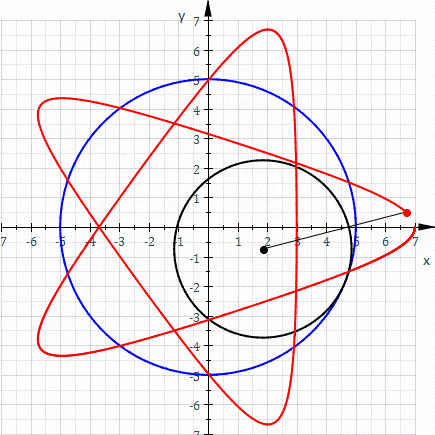
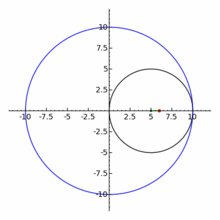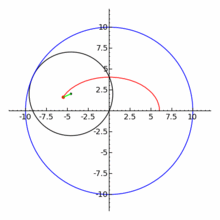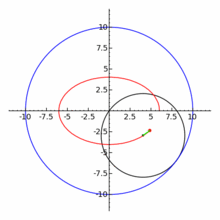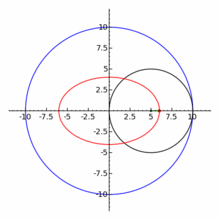
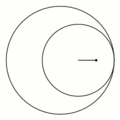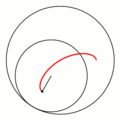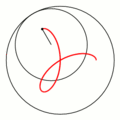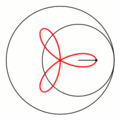
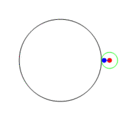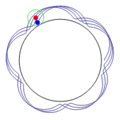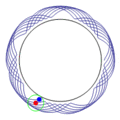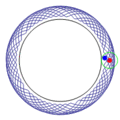
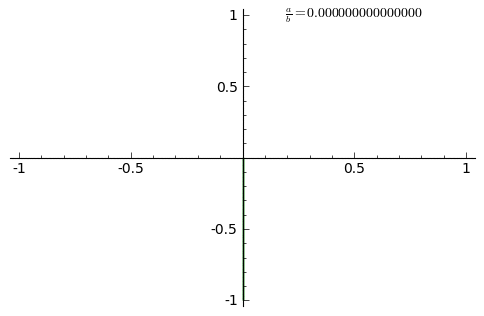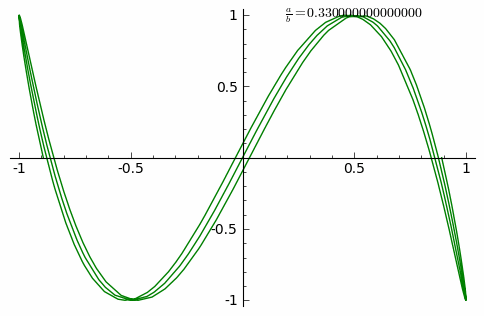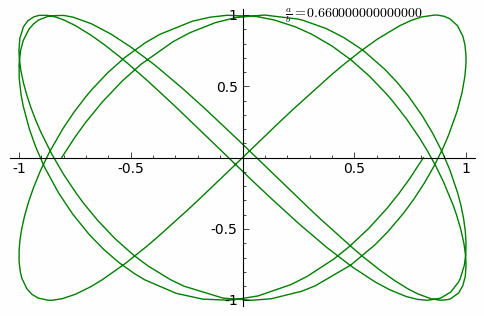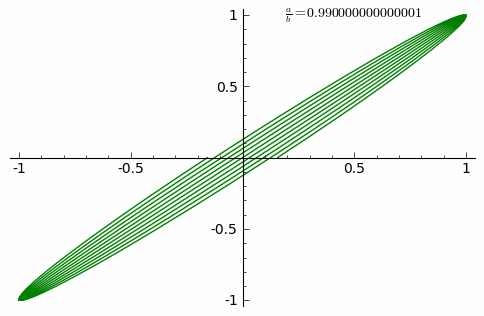一八一五年納撒尼爾‧鮑迪奇 Nathaniel Bowditch 首先研究了『一族曲線』,它是兩個沿著『互相垂直』方向的『正弦振動』之合成的『軌跡』。一八五七年朱爾‧安托瓦內‧利薩茹 Jules Antoine Lissajous 作了詳細研究。他同時利用『一束光』射向固定在一個『音叉』上的『鏡子』,再將『反射光』又導往固定在另一個『音叉』上的一面『鏡子』,之後的這一個音叉的振動方向與之前的那一個垂直,一般所使用的振動頻率也不同,最終反射光就在牆上形成了今天所說的『利薩茹圖形』。假使從『音樂』的角度來看,這就是兩個『音符』同奏或接續時,所產生的一種特定的『頻率』harmonic interval 之間『和諧』與否的關係!!
數學上,利薩茹 Lissajous 曲線可以用『參數方程式』表示為
![]()
![]()
這族曲線的『外貌』與兩個振動之『頻率比』![]() 有很大的關係。如果它是最簡『有理數』
有很大的關係。如果它是最簡『有理數』![]() ,此處
,此處 ![]() 是自然數,這條曲線是靜止『封閉的』,在
是自然數,這條曲線是靜止『封閉的』,在 ![]() 軸上有
軸上有 ![]() 個『波瓣』,以及在
個『波瓣』,以及在 ![]() 軸上有
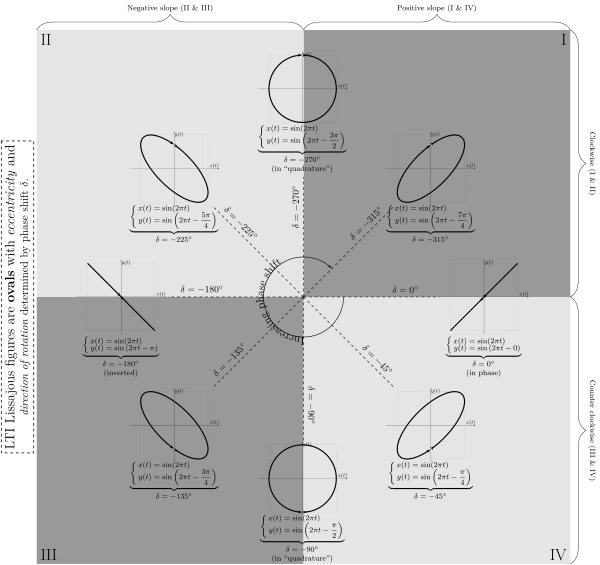
軸上有 ![]() 個『波瓣』。假使比值是『無理數』,這條曲線看起來在『旋轉』。兩振動的『振幅』之比值
個『波瓣』。假使比值是『無理數』,這條曲線看起來在『旋轉』。兩振動的『振幅』之比值 ![]() 確定了此曲線相對的『長與寬』;兩振動之間的『相位差』
確定了此曲線相對的『長與寬』;兩振動之間的『相位差』 ![]() 決定了曲線外貌的『旋轉角』。
決定了曲線外貌的『旋轉角』。
傳說中畢達哥拉斯發現『音律』有一段美麗的故事。有一天他偶然經過『打鐵鋪』店門口,卻為『打鐵』時有『節奏』而且『悅耳』的聲音所吸引。他感覺到很『驚奇』,於是走進了鋪中『觀察』,『研究』後發現四個『打鐵錘』的『重量比』恰為 『12:9:8:6』。假使將之兩兩一組拿來敲打,『12: 6= 2:1』、『12 : 8 = 9:6 = 3:2』和『12:9=8:6=4:3』的組合都能發出『和諧』的聲音。之後畢達哥拉斯更進一步用『弦琴』來做『實驗』並且加以『驗證』,這就是著名之『弦琴律』的由來!!
如果在一台『示波器』上 ![]() 輸入
輸入 ![]() 軸信號,
軸信號,![]() 輸入
輸入 ![]() 軸信號,這時你就可以用示波器來觀察它所顯示的曲線,並且衡量出這兩個信號的『頻率比』以及『相位差』。在專業聲音的領域,通常利薩茹曲線用來分析『左右』聲道的『立體聲信號』stereo audio signal 之間的『相位關係』。假使你正研究一個『線性非時變系統』的『電路』,因此『輸入信號』的頻率就一定會與『輸出信號』的頻率『相同』。由於物理的『因果原理』要求『輸出信號』發生在『輸入信號』之後,所以輸出入間的『相位關係』將如左圖所示,應當都是『負值』。這個情況下,你可以相當『精確』的『測量』相位差,也就是說這個 LTI 系統的『響應遲延』。
軸信號,這時你就可以用示波器來觀察它所顯示的曲線,並且衡量出這兩個信號的『頻率比』以及『相位差』。在專業聲音的領域,通常利薩茹曲線用來分析『左右』聲道的『立體聲信號』stereo audio signal 之間的『相位關係』。假使你正研究一個『線性非時變系統』的『電路』,因此『輸入信號』的頻率就一定會與『輸出信號』的頻率『相同』。由於物理的『因果原理』要求『輸出信號』發生在『輸入信號』之後,所以輸出入間的『相位關係』將如左圖所示,應當都是『負值』。這個情況下,你可以相當『精確』的『測量』相位差,也就是說這個 LTI 系統的『響應遲延』。
在沒有『示波器』的時代,有一種使用『單擺』的機械『繪圖工具』,稱之為『諧振記錄器』harmonograph。大約在十九世紀中葉出現,傳聞是英國蘇格蘭格拉斯哥大學 University of Glasgow 數學教授休‧布来克本 Hugh Blackburn 所發明的。一個簡單『橫向的』 lateral 諧振記錄器上的兩個『阻尼單擺』運動方程式,可以數學上表示為
![]()
![]()
,式中 ![]() 是『幅度大小』、
是『幅度大小』、![]() 是『角頻率』、
是『角頻率』、![]() 是『相位角』以及
是『相位角』以及 ![]() 為『阻尼常數』。在這個裝置上
為『阻尼常數』。在這個裝置上 ![]() 控制『繪圖筆』的
控制『繪圖筆』的 ![]() 軸運動,
軸運動,![]() 控制『繪圖板』的
控制『繪圖板』的 ![]() 軸運動,通常繪出的圖形也是『利薩茹』一類的相關曲線。
軸運動,通常繪出的圖形也是『利薩茹』一類的相關曲線。
二零一一年 JM Gustafson 先生發表了一個『虛擬的』諧振記錄器模擬軟體,有興趣的讀者可以到那兒去『玩玩』,嘗試設計不同的『單擺參數』,『創造』自己喜歡的『美麗曲線』!!
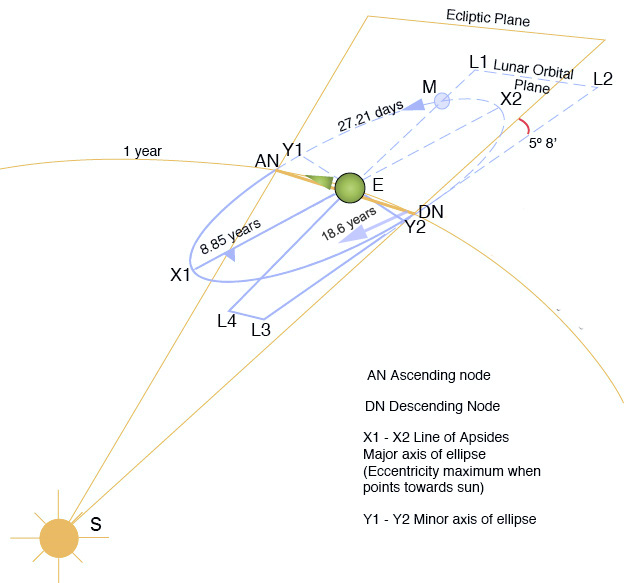
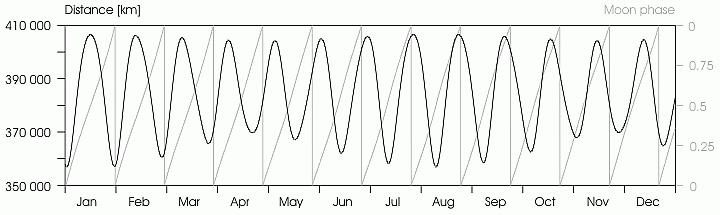
地球繞著太陽轉,月亮繞著地球轉。兩個週期運動耦合起來,卻是複雜萬端。月球軌道以二十七點三二天環繞地球一周。地球和月球的質心在距地心四千七百公里處,各自圍繞著質心運轉。月球與地球中心的平均距離是三十八萬五千公里,約為地球半徑的六十倍。軌道的平均速度是一千零二十三公里/秒,月球在恆星背景上大約每小時移動 0.5°,軌道的平均離心率是0.0549。非圓形的軌道導致從大地上賞月時,視直徑的大小和角速度上都有著顯著的變化。對一位假想在質心上的觀測者而言,月球每天的平均角位移量是向東 13. 176358°,然而軌道的指向在空間中卻不固定,而是隨著時間不斷的進動;其一是拱點線的進動,橢圓形的月球軌道慢慢的逆時鐘方向轉動,一周需要三千兩百三十三天。另一是月球軌道與黃道的交點對的進動,一圈長達十八點六年。
果真簡諧運動的耦合,也許是和諧的,未必是簡單的!!
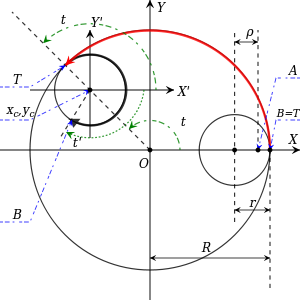
一八八零年代波蘭數學家 Bruno Abakanowicz 發明了『螺旋圖』Spirograph 。一九六四年英國工程師德尼斯‧費舍爾 Denys Fisher 發現使用多種『大小比值』不同的兩個內外『圓形齒輪』,當『內小圓形齒輪』上不同的『筆洞位置』在『外大圓形齒輪』上『循著圓周』轉動時,可以畫出各種美麗的『內旋輪線』 hypotrochoid 以及『外旋輪線 』epitrochoid。在經過一番齒輪『大小比值』與筆洞『位置比值』的研究後,費舍爾於隔年一九六五年的德國 Nuremberg 國際玩具展將之發表上市。由於它所繪出的『圖案』令人聯想到『萬花筒』 ,所以被我們叫做『萬花尺』。這是一個曾經『流行』過的『益智玩具』,其實它是了解『周期運動』組合的『複雜性』很好的『工具』。萬花尺內旋輪線的參數方程式可以表示為
![Rendered by QuickLaTeX.com \begin{array}{rcl} x(t)&=&R\left[(1-k)\cos t+lk\cos \frac{1-k}{k}t\right] ,\\[4pt] y(t)&=&R\left[(1-k)\sin t-lk\sin \frac{1-k}{k}t\right] .\\\end{array}](http://www.freesandal.org/wp-content/ql-cache/quicklatex.com-ea77aa476c55506d41f7e14c0473dc7c_l3.png)
此處 ![]() 是『外大齒輪』的半徑,
是『外大齒輪』的半徑,![]() 是大小齒輪的『半徑比』
是大小齒輪的『半徑比』 ![]() ,
,![]() 是筆洞所在位置到『內小齒輪』圓心的距離與『內小齒輪』半徑的比值
是筆洞所在位置到『內小齒輪』圓心的距離與『內小齒輪』半徑的比值 ![]() 。
。
網路上有一個『Spirograph Art』的網頁,假使讀者有興趣的話,不妨前去看看。