樹莓派、樹莓派之學習、樹莓派之教育

【Sonic π】電聲學補充《三》上

220px-Early_Pinball

彈珠台

200px-Electrona_in_crystallo_fluentia.svg

德國物理學家保羅‧卡爾‧路德維希‧德汝德 Paul Karl Ludwig Drude 於一九零零年提出了一個『電傳導』的模型。他想從『微觀』的角度來推導『歐姆定律』。雖然在今天或許需要一些量子力學的修正，這個古典簡單的模型卻提供了『金屬』中『直流電』和『交流電』的傳導、磁場的『霍爾效應』，以及『熱傳導』種種現象非常好的解釋。

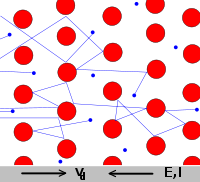
德汝德將『導體』想像成由相對固定的『正離子』與可移動的『自由電子』所構成。這些為數眾多的『自由電子』彼此間不斷的發生『碰撞』，又和固定的『正離子』間也發生碰撞，彷彿就像在『彈珠台』裡的那些『彈珠』一樣。那麼到底這些『自由電子』的數量有多大的呢？如果用 D_e 代表『電子密度』，D_e = N_A \frac{Z_c \rho_m}{A_m}，此處 N_A = 6.02 \times {10}^{23} 是阿佛加德羅常數，Z_c 是一個金屬原子貢獻多少個『自由電子』，\rho_m 是金屬質量密度，A_m 是金屬的原子量。

舉例來說『鈉』 Na 很容易形成一價的『鈉離子』， 就說它的 Z_c = 1，如此 D_{eNa} = 6.02 \times {10}^{23} atoms/mole \frac {1 e / atom \cdot 0.968 \times {10}^6 g / m^3}{22.98 g/mole} = 2.54 \times {10}^{28} e / m^3，這樣一克的鈉，體積大約一立方公分，就有『數量級』為 {10}^{22} 個『自由電子』。

假使將它看成『自由電子氣體』，再利用奧地利物理學家路德維希‧愛德華‧波茲曼 Ludwig Eduard Boltzmann 所發展的古典氣體『運動理論』Kinetic theory 來探討這些『自由電子』，就如同理想氣體一樣，在『熱平衡』時，一個『自由電子』的『熱速度』 v_{thermal}  可以用 \frac {1} {2} m \cdot \overline{{v_{thermal}}^2} = \frac {3} {2} k_B T 來計算，此處 k_B 是波茲曼常數 k_b = 1.3806488(13) \times 10^{-23} \mbox{ JK}^{-1}， T 是『絕對溫標』。那麼室溫下 {25}^{\circ} C = {298.16}^{\circ} K 的一個『自由電子』的『熱速度』大約是 v_{thermal} = \sqrt{\frac {3 k_B T}{m}} = 1.16 \times {10}^5 m/s。

225px-Boltzmann2
統計力學拓荒者

Translational_motion

這個速度一秒大於百公里，不可謂之不大，假使用『費米氣體』的量子統計力學來講，更要大上個十倍，不過由於它在『各方向』的『均等性』，因此統計上來說『淨電流』的貢獻為『零』。也就是說 \langle \vec{v}_{thermal} \rangle = 0。

那麼德汝德是如何看待這些『碰撞』作用的呢？或者說他做了哪些『假設』的呢？這點正是探討一個『物理模型』的『合理性』與『適切性』的重要之處。依據現今的說法，德汝德假設了︰

一、如果沒有外部的『電磁場』作用，『自由電子』將會作『直線運動』，彼此間的『電磁作用力』可以被忽略。這意味著是一種『獨立電子』的假設，它處於一個由『正離子』與『其他電子』所構成的『平均的環境』 ── 因此淨作用為零 ──，統計上來講這一般認為是『合宜的』。

二、『電子』和『正離子』之間的『碰撞』是『即時』的，統計上無關之『隨機事件』，所以總體來說這沒有任何『淨貢獻』，雖然有不同的學者『批評』它的『合宜性』。然而如果從『散射事件』來看，這也許只是說某些『物質屬性』之『均向性』的另一種說法罷了。

三、假設了『平均碰撞時間』 \tau 的『存在』，所以我們可以說很小的一段時距 \delta t 發生『碰撞』的『機會』是 \frac {\delta t}{\tau}，而且這個『機率』和一個『自由電子』的『位置』與『動量』無關。這正像是『丟一根』長度為 \delta t 的『針』投到一個以 \tau 為『格子線』板子上，問『針』掉到『線上』的『機率』大小如何，通常被認為是很好的『近似』。

四、『碰撞』後的『熱電子』應該保有該處『熱平衡』的速度。這是一個作用『鄰近原則』的假設，一般從『物理因果』上講，以為應是『正確的』。

那麼我們如何推導『自由電子』受到一個外在時變的『力場』 \vec{F}(t) 中之『平均動量』方程式的呢？假使在 t 時刻，一個『自由電子』的『動量』是 \vec{p}(t)，到了 t + dt 時刻它的動量 \vec{p}(t+dt) 可以這樣考慮，如果說這個『自由電子』發生了『碰撞』，按造『假設三』它的『碰撞』機率是 P_c = \frac{dt}{\tau}，再依據『假設二』，它的淨『平均動量』貢獻將會是『零』， \langle {\vec{p}}_c(t+dt) \rangle = 0。如果說此時這個『自由電子』沒有發生『碰撞』，於是按造『牛頓第二運動定律』\langle {\vec{p}}_{nc}(t+dt) \rangle = \langle \vec{p}(t) \rangle + \vec{F}(t)dt，這個不發生『碰撞』的機率 P_{nc} 是 1 - P_c = 1 - \frac{dt}{\tau}，因此

\langle \vec{p}(t+dt) \rangle = P_c \cdot \langle {\vec{p}}_c(t+dt) \rangle + P_{nc} \cdot \langle {\vec{p}}_{nc}(t+dt) \rangle

= \left( 1 - \frac{dt}{\tau} \right) \left( \langle \vec{p}(t) \rangle + \vec{F}(t)dt \right)，所以可得

\frac{d \langle \vec{p}(t) \rangle}{dt} = \frac{\langle \vec{p}(t+dt) \rangle - \langle \vec{p}(t) \rangle}{dt} = - \frac{\langle \vec{p}(t) \rangle}{\tau} + \vec{F}(t)。

這就是德汝德模型之電子的運動方程式。首先我們考慮一些典型的『時變力場』\vec{F}(t) 情況︰

一、沒有外力存在 \vec{F}(t) = 0 時，\langle \vec{p}(t) \rangle = \langle \vec{p}(0) \rangle \cdot e^{- \frac {t}{\tau}}，這說明了『弛豫時間』 Relaxation Time \tau 的物理意義，每經過 \tau 時距，『平均動量』以 e^{-1} 為比率『衰減』。事實上，電子的運動方程式中的 - \frac{\langle \vec{p}(t) \rangle}{\tau} 項就是一種『阻力』的啊！

二、常量不隨時變的外力 \vec{F} 時，\langle \vec{p}(t) \rangle = \langle \vec{p}(0) \rangle \cdot e^{- \frac {t}{\tau}} + \vec{F} \cdot \tau。當 t >> \tau 時，『暫態解』可以被忽略，這時 \langle \vec{p}(t) \rangle = \vec{F} \cdot \tau。假使將此應用於『導體』中的電子在一個『均勻恆定的電場』 \vec{E} 情況下，這時 \langle \vec{p}(t) \rangle = e \cdot \vec{E} \cdot \tau，由於

\langle \vec{p}(t) \rangle = m \cdot \langle \vec{v}(t) \rangle，

\vec{J} = D_e \cdot e \langle \vec{v}(t) \rangle

，於是就得到了 \vec{J} = \left( \frac{D_e e^2 \tau}{m} \right) \vec{E}，也就是說電流密度 \vec{J} 與電場 \vec{E} 成正比，這就是『歐姆定律』的『微觀表述』。通常人們將『電場』作用下的電子『平均速度』稱作『漂移速度』 Drift Velocity，那麼這個『漂移速度』有多大的呢？如果考慮一根直徑一公釐的銅線，因為銅的密度是每立方公分 8.94 克，它的莫爾原子量是 63.546 克，所以假設每個銅原子貢獻一個自由電子，那麼一立方公尺的銅，就有 8.5 * 10^{28} 個自由電子。假使這根銅線上流過 3 A 安培的電流，『漂移速度』可以用下式來計算

v = {I \over nAq}

v = \frac{3}{\left(8.5 \times 10^{28}\right) \left(7.85 \times 10^{-7}\right) \left(-1.6 \times 10^{-19}\right)}

v = -0.00028

上式中，I 是電流量，n 是電流密度，A 是銅線的截面積，q 是電子的電荷量，因次分析的結果是︰

v = \dfrac{\text{A}}{\dfrac{\text{electron}}{\text{m}^3}{\cdot}\text{m}^2\cdot\dfrac{\text{C}}{\text{electron}}} = \dfrac{\text{C}}{\text{s}{\cdot}\dfrac{1}{\text{m}}{\cdot}\text{C}} = \dfrac{\text{m}}{\text{s}}

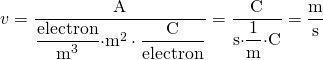
，由此可知『電子』在電場中的『漂移速度』如果和『熱速度』作比較其實是非常的小。那麼『電流』的『速度』到底有多快的呢？『電子』果真會從『電力公司』長途跑到『你家裡』的嗎？？

 

─── 待續……