【Sonic π】電聲學之電路學《四》之《 V!!》

玉連環

九連環

Baguenaudier

《戰國策‧卷十三》

齊閔王之遇殺，其子法章變姓名，為莒太史家庸夫。太史敫女，奇法章之狀貌，以為非常人，憐而常竊衣食之，與私焉。莒中及齊亡臣相聚，求閔王子，欲立之。法章乃自言於莒。共立法章為襄王。襄王立，以太史氏女為王后，生子建。太史敫曰：『女無謀而嫁者，非吾種也，汙吾世矣。』終身不睹。君王后賢，不以不睹之故，失人子之禮也。

襄王卒，子建立為齊王。君王后事秦謹，與諸侯信，以故建立四十有餘年不受兵。

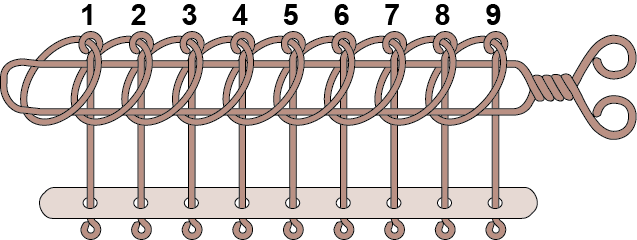
秦始皇嘗使使者遺君王后玉連環，曰：『齊多知，而解此環不？』君王后以示群臣，群臣不知解。君王后引椎椎破之，謝秦使曰：『謹以解矣。』

及君王后病且卒，誡建曰：『群臣之可用者某』。建曰：『請書之。』君王后曰：『善。』取筆牘受言。君王后曰：『老婦已亡矣！』

君王后死，後后勝相齊，多受秦間金玉，使賓客入秦，皆為變辭，勸王朝秦，不脩攻戰之備。

『卓文君』為四川臨卭巨商卓王孫之女，姿嬌貌美，精通音律，善彈琴，富文采。司馬相如到卓王孫家裡赴宴，聞知『文君新寡』，便奏了一曲《鳳求凰》，於是夜『連夜私奔』逃到了成都。

傳說她倆也曾過得幾年鴛鴦生活，據聞當司馬相如在長安，被封為中郎將時，自覺身份已是不凡，興起休妻的念頭，便寫了一封『數字信』︰一二三四五六七八九十百千萬；且囑送信人必得帶回『回信』。冰雪聰明『卓文君』頓然識破乃『無億』也，是『無憶』又『無意』的啊！於是回了封《怨郎詩》給司馬相如：

一別之後，二地相思，只說三四月，又誰知五六年。七弦琴無心彈，八行書無可傳，九連環從中折斷，十里長亭望眼欲穿。百思量，千繫念，萬般無奈把郎怨。萬語千言說不完，百無聊賴十依欄，重九登高看孤雁，八月中秋月圓人不圓。七月半燒香秉燭問蒼天，六月伏天人人搖扇我心寒。五月石榴如火偏遇陣陣冷雨澆花端，四月枇杷未黃我欲對鏡心意亂，三月桃花隨水轉，飄零零，二月風箏線兒斷。噫，郎呀郎，巴不得下一世你為女來我為男。

這一千古奇聞，至今考證不完。

《西京雜記》
眉色如望遠山，
臉際常若芙蓉，
肌膚柔滑如脂。

《白頭吟》卓文君

皚如山上雪，　皎若雲間月。
聞君有兩意，　故來相決絕。
今日斗酒會，　明旦溝水頭。
躞蹀御溝上，　溝水東西流。
淒淒復淒淒，　嫁娶不須啼。
願得一心人，　白頭不相離。
竹竿何嫋嫋，　魚尾何簁簁。
男兒重意氣，　何用錢刀為。

於是乎『九連環』出自何時何處誰人之手，眾說紛紜『莫宰羊』矣。『惠施』一句【連環可解也。】是『可解』是『不可解』的呢？『攻玉石』而得『玉連環』本來自『一石』，秦國之意明矣，非在問『智』，以『技力』『威』之也，而『君王后』引『椎』『破』之，是知其『不可解』，寧可『玉碎』以為之『解』，乃『不畏刀兵』之意也明矣。一九三一年時，『哥德爾』發表了兩條『哥德爾不完備定理』︰

一、任何『相容』的形式系統，只要蘊涵著『皮亞諾算術公理』，就一定可以在之中構造出體系裡既『不能證明』也『不能否證』的『命題』，也就是說那個體系是『不完備』的。

二、任何『相容』的形式系統，只要蘊涵著『皮亞諾算術公理』，它就無法用此來證明它自身的『相容性』。

由此看來若是『連環』出自『天工』，自是『無縫而成』，自然就『無可解』，那麼『惠施』的時代果真已有『九連環』的嗎？假使那時真有『九連環』的話，『惠施』此言又在說什麼呢？？或許以『名家思辨』揣想『既然可順以成連環，必然可逆之解連環』，也許這就是『惠施』所說的【連環可解也。】之理的吧！這個『順逆操作觀』就是理解『九連環數學』的關鍵。據聞，西方人多以為『九連環』是『諸葛孔明』所作，因他經年帶兵打仗，為排遣妻子寂寞而發明。之後，那個講『梵天寺』之『浮屠』── 塔 ──的傳說之法國數學家『Édouard Lucas』最早用『二進制』觀點，給出了 $n$ 連環的最少步驟之『一般解』︰

$a(n) = \begin{cases} \frac{2^{n+1}-2}{3}, & \text{when }n\text{ is even,}\\ \frac{2^{n+1}-1}{3}, & \text{when }n\text{ is odd.}\end{cases}$ 。

解之前

解之中

解之後

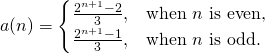就讓我們略探一下『九連環』之奧妙的吧！假使用『圖靈機』的『狀態操作觀』來看，『N 連環』的『狀態』可以用 $[r_n, r_{n-1}, \cdots , r_k, \cdots, r_1]$ 所表示， $r_k = 0$ 代表 $k$ 『位置』上『無環』， $r_k = 1$ 就是說 $k$ 『位置』上『有環』。依其『形制』，除了『第一環』它隨時可以『套上柄』 $[r_n, r_{n-1}, \cdots , r_k, \cdots, r_2, 1]$ 或是『卸下柄』 $[r_n, r_{n-1}, \cdots , r_k, \cdots, r_2, 0]$ 之外。『其餘環』 $i$ 皆得只有『前環在』 $i-1$ ，又得『其前無環』方得『上、下』，也就是說 $k$ 環之上下，必得於 $[r_n, r_{n-1}, \cdots , r_k, 1, 0, \cdots, 0, 0]$ 之時。於是乎，欲解『N 連環』就得要『倒著解』，必先將『最後環』來『卸下柄』，再『及其次』以至於『至其一』而後『解』。

古有『口訣』言︰相『陰陽』始『陰陽』，續用『陽陰』交互使，下下上上『有時盡』，千重連環『終可解』！！

若問『步數』是『幾何』？欲解『第 N 環』 $R_n$ 須先解前『N – 2 之環』 $R_{n-2}$ ，至此僅存『二連環』，故可『卸下』那『第 N 環』，一過此步 $+1$ 祇剩 $N-1$ 之『那一環』，欲解之，又得『套上』前『N – 2 之環』 $R_{n-2}$ 那些環，後再解此下『N-1 之連環』 $R_{n-1}$ 的啊！由是故得