如果人們已經知道『五次以上』之方程式沒有『多次方根』形式的一般解︰
概念的由來並非是無根之木突然結果,自有歷史的淵源,比較像鐵樹開花,基礎之因和境遇之緣的偶遇,彷彿一道閃光劃破天際 ,於是人們就知道了雷聲不遠的了。
在『群論』 group theory 的歷史上,兩位重要的興起者,或許因為不同的環境因素,都發生不幸的早夭事件。其一是挪威數學家尼爾斯‧亨利克‧阿貝爾 Niels Henrik Abel 生於一八零二年,一八二五年得到政府之資助,始得遊學柏林和巴黎。由於生前不得志,現實裡一直無法獲得教席而能專心的研究,最終在一八二九年,因肺結核在 挪威的弗魯蘭病世。就在死後兩天,家中收到了來自柏林的聘書。阿貝爾他以證明五次方程式『不可能』用『多次方根形式』 ![]() 的一般解與對於『橢圓函數論』的研究而聞名於世。
的一般解與對於『橢圓函數論』的研究而聞名於世。
法國著名的數學家埃瓦里斯特‧伽羅瓦 Évariste Galois 生於一八一一年,當他還是十多歲的青年之時,他就已經發現了 N 次多項式可以用『根式解』的『充份必要條件』,這解決了長期困擾數學界的問題。伽羅瓦是第一個使用『群』 group 這一個術語的人。據聞他是一位激進的共和主義者,在路易‧菲利普復辟的時期被捕入獄。一八三二年時,伽羅瓦於出獄後,在一次幾乎自殺式的決鬥中喪了命,此事件的起因引起了多方各種的揣測??在今天他與阿貝爾並稱為『現代群論』的創始人 。
過去大數學家『歐拉』曾經著書立論,強調新的數學常常是起源於『觀察』與『實驗』。那麼伽羅瓦和阿貝爾他們又在觀察『什麼』的呢?假使思考 N 階『多項式』和 N 次『方程式』的『融會處』
![]()
,此處 ![]() 是『有理數』,
是『有理數』,![]() 是對應的『根』。
是對應的『根』。
那麼當時果真已經證明了 N 次『方程式』就有 N 個解的嗎?其實並非如此,然而『三次』與『四次』方程式求解的一般的『方法』大概已經知道了。這又和『五次』方程式能不能求解有什麼關係的呢?就樣我們就從 ![]() 是『有理數』嗎開始,也許可以窺見一斑。為什麼說
是『有理數』嗎開始,也許可以窺見一斑。為什麼說 ![]() 『不可能』是『有理數』的呢?因為它不可能『表達』成『有理數』的『形式』
『不可能』是『有理數』的呢?因為它不可能『表達』成『有理數』的『形式』 ![]() ,一般約定的說此處
,一般約定的說此處 ![]() 與
與 ![]() 是整數而且互質。如果依據『歐幾里得』的證法,假使講一個有理數
是整數而且互質。如果依據『歐幾里得』的證法,假使講一個有理數 ![]() 的『因式分解』,沒有任何一個『質因子次方』大於二 ── 其內沒有平方數 ──,那麼這個
的『因式分解』,沒有任何一個『質因子次方』大於二 ── 其內沒有平方數 ──,那麼這個 ![]() 也就必然不會是『有理數』的了。這又是為什麼呢?因為假設
也就必然不會是『有理數』的了。這又是為什麼呢?因為假設 ![]() ,就可以得到
,就可以得到 ![]() ,然而因為
,然而因為 ![]() 『互質』,所以
『互質』,所以 ![]() ,而且
,而且 ![]() 也『互質』,這樣又可以得到
也『互質』,這樣又可以得到 ![]() ,因此
,因此 ![]() 就一定是當然的了,於是
就一定是當然的了,於是 ![]() 和
和 ![]() 就有了共同『因子』
就有了共同『因子』 ![]() ,這卻產生了『假設矛盾』,因是之故,『歸謬』的得出了
,這卻產生了『假設矛盾』,因是之故,『歸謬』的得出了 ![]() 不是『有理數』。那麼當我們談及
不是『有理數』。那麼當我們談及 ![]() 時,這裡所說的『多項式』與『方程式』是一樣的嗎?它們的內在聯繫又是什麼的呢?
時,這裡所說的『多項式』與『方程式』是一樣的嗎?它們的內在聯繫又是什麼的呢?
── 摘自《【Sonic π】電路學之補充《四》無窮小算術‧中下下‧上》
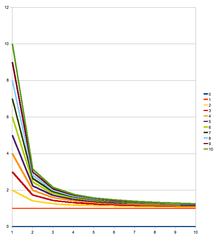
為何繼續探究『白努利多項式序列』 ![]() 之『根』呢?
之『根』呢?
乃今這個序列又稱之為『阿佩爾序列』
Appell sequence
In mathematics, an Appell sequence, named after Paul Émile Appell, is any polynomial sequence {pn(x)}n = 0, 1, 2, … satisfying the identity
and in which p0(x) is a non-zero constant.
Among the most notable Appell sequences besides the trivial example { xn } are the Hermite polynomials, the Bernoulli polynomials, and the Euler polynomials. Every Appell sequence is a Sheffer sequence, but most Sheffer sequences are not Appell sequences.
Equivalent characterizations of Appell sequences
The following conditions on polynomial sequences can easily be seen to be equivalent:
- For n = 1, 2, 3, …,
- and p0(x) is a non-zero constant;
- For some sequence {cn}n = 0, 1, 2, … of scalars with c0 ≠ 0,
- For the same sequence of scalars,
- where
- For n = 0, 1, 2, …,
應是開拓者有所得乎?『真理』面前人人『平等』,『思路』之內各各『不同』。某人之『解題方法』果真是其人之『神經網絡』的『獨特通道』耶??抑或是來自於外乎其身的大千世界之『經驗』 也!難到不可是『生而知之』嗎!!故而令人『好奇』了☆
此所以說起『讀書學習』乙事!喜歡依著次序、按部就班,好乎?不好耶 ??作者反省反思之後,以為『各適其性』矣☆
於是特說在前,提筆落處未必『重點』,輕描淡寫也許『關鍵』,只是隨著自己的『思路』感覺,希望讀者容易『理解』,信筆寫去而已。
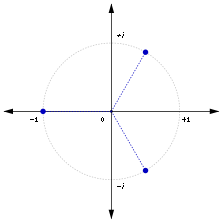
因此直言曰︰那個『奇次』的白努利多項式,看來於 ![]() 、
、 ![]() 、
、 ![]() 都是『其根』??!!
都是『其根』??!!
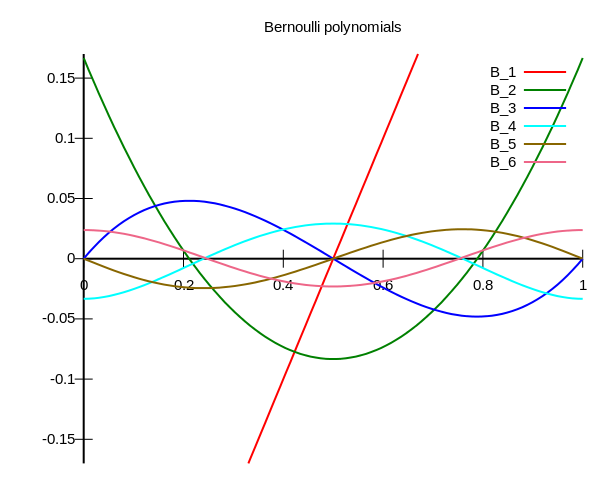
,首要就是『知道』如何計算 ![]() 的呀!! ??
的呀!! ??