針對『響度』循名責實,終究把我們帶回『聲壓』這個物理概念︰
Sound pressure
Sound pressure or acoustic pressure is the local pressure deviation from the ambient (average or equilibrium) atmospheric pressure, caused by a sound wave. In air, sound pressure can be measured using a microphone, and in water with a hydrophone. The SI unit of sound pressure is the pascal (Pa).[1]
Mathematical definition
A sound wave in a transmission medium causes a deviation (sound pressure, a dynamic pressure) in the local ambient pressure, a static pressure.
Sound pressure, denoted p, is defined by
where
- ptotal is the total pressure;
- pstat is the static pressure.
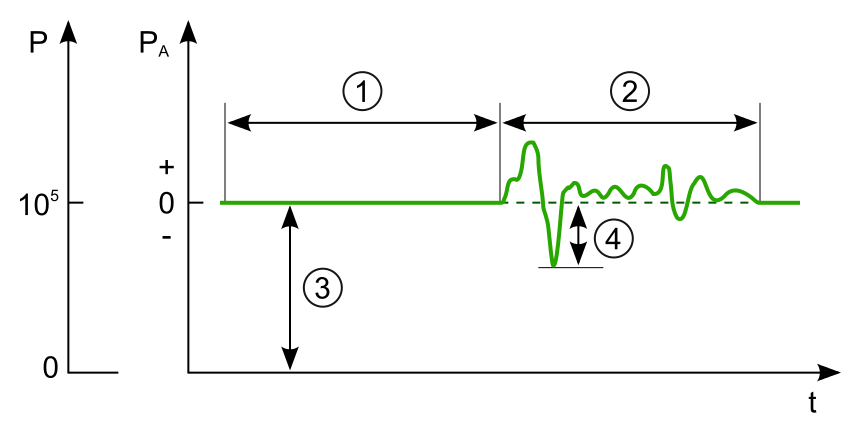
Sound pressure diagram:
- silence;
- audible sound;
- atmospheric pressure;
- sound pressure
…
Sound measurements
Sound intensity
In a sound wave, the complementary variable to sound pressure is the particle velocity. Together, they determine the sound intensity of the wave.
Sound intensity, denoted I and measured in W·m−2 in SI units, is defined by
where
- p is the sound pressure;
- v is the particle velocity.
……
Inverse-proportional law
When measuring the sound pressure created by an object, it is important to measure the distance from the object as well, since the sound pressure of a spherical sound wave decreases as 1/r from the centre of the sphere (and not as 1/r2, like the sound intensity):[3]
This relationship is an inverse-proportional law.
If the sound pressure p1 is measured at a distance r1 from the centre of the sphere, the sound pressure p2 at another position r2 can be calculated:
The inverse-proportional law for sound pressure comes from the inverse-square law for sound intensity:
Indeed,
where
- ∗
is the convolution operator;
- z −1 is the convolution inverse of the specific acoustic impedance,
hence the inverse-proportional law:
The sound pressure may vary in direction from the centre of the sphere as well, so measurements at different angles may be necessary, depending on the situation. An obvious example of a sound source whose spherical sound wave varies in level in different directions is a bullhorn.[citation needed]
………
Sound pressure level
Sound pressure level (SPL) or acoustic pressure level is a logarithmic measure of the effective pressure of a sound relative to a reference value.
Sound pressure level, denoted Lp and measured in dB, is defined by[4]
where
- p is the root mean square sound pressure;[5]
- p0 is the reference sound pressure;
- 1 Np is the neper;
- 1 B = (1/2 ln 10) Np is the bel;
- 1 dB = (1/20 ln 10) Np is the decibel.
The commonly used reference sound pressure in air is[6]
which is often considered as the threshold of human hearing (roughly the sound of a mosquito flying 3 m away). The proper notations for sound pressure level using this reference are Lp/(20 μPa) or Lp (re 20 μPa), but the suffix notations dB SPL, dB(SPL), dBSPL, or dBSPL are very common, even if they are not accepted by the SI.[7]
Most sound level measurements will be made relative to this reference, meaning 1 Pa will equal an SPL of 94 dB. In other media, such as underwater, a reference level of 1 μPa is used.[8] These references are defined in ANSI S1.1-1994.[9]
………
Multiple sources
The formula for the sum of the sound pressure levels of n incoherent radiating sources is
Inserting the formulas
in the formula for the sum of the sound pressure levels yields
藉此我們將更了解 MIR
The energy (Wikipedia; FMP, p. 66) of a signal corresponds to the total magntiude of the signal. For audio signals, that roughly corresponds to how loud the signal is. The energy in a signal is defined as
![]()
The root-mean-square energy (RMSE) in a signal is defined as
![]()
筆記的內容!能夠區分它與『物理能量』之異同?
Energy (signal processing)
In signal processing, the energy of a continuous-time signal x(t) is defined as
the energy of a discrete-time signal x(n) is defined as
Relationship to energy in physics
Energy in this context is not, strictly speaking, the same as the conventional notion of energy in physics and the other sciences. The two concepts are, however, closely related, and it is possible to convert from one to the other:
-
- where Z represents the magnitude, in appropriate units of measure, of the load driven by the signal.
For example, if x(t) represents the potential (in volts) of an electrical signal propagating across a transmission line, then Z would represent the characteristic impedance (in ohms) of the transmission line. The units of measure for the signal energy would appear as volt2·seconds, which is not dimensionally correct for energy in the sense of the physical sciences. After dividing
by Z, however, the dimensions of E would become volt2·seconds per ohm, which is equivalent to joules, the SI unit for energy as defined in the physical sciences.
倘使再讀點 Make 麥克風量測文章
12/7/2017》
回顧 ReSpeaker 4Mic 規格︰
無論打算拿 ReSpeaker 4-Mic Array

的麥克風做什麼?最好能先知道它的規格。
於是考察其電路圖︰
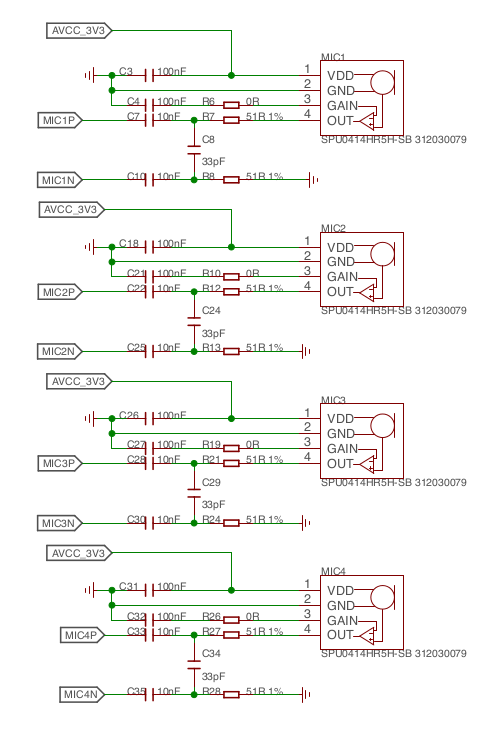
得知使用 SPU0414HR5H-SB 也。



─── 摘自《【鼎革‧革鼎】︰ Raspbian Stretch 《六之 I 》》
或可思
recognizer_instance.energy_threshold = 300 # type: float
Represents the energy level threshold for sounds. Values below this threshold are considered silence, and values above this threshold are considered speech. Can be changed.
This is adjusted automatically if dynamic thresholds are enabled (see recognizer_instance.dynamic_energy_threshold). A good starting value will generally allow the automatic adjustment to reach a good value faster.
This threshold is associated with the perceived loudness of the sound, but it is a nonlinear relationship. The actual energy threshold you will need depends on your microphone sensitivity or audio data. Typical values for a silent room are 0 to 100, and typical values for speaking are between 150 and 3500. Ambient (non-speaking) noise has a significant impact on what values will work best.
If you’re having trouble with the recognizer trying to recognize words even when you’re not speaking, try tweaking this to a higher value. If you’re having trouble with the recognizer not recognizing your words when you are speaking, try tweaking this to a lower value. For example, a sensitive microphone or microphones in louder rooms might have a ambient energy level of up to 4000:
import speech_recognition as sr r = sr.Recognizer() r.energy_threshold = 4000 # rest of your code goes here
The dynamic energy threshold setting can mitigate this by increasing or decreasing this automatically to account for ambient noise. However, this takes time to adjust, so it is still possible to get the false positive detections before the threshold settles into a good value.
To avoid this, use recognizer_instance.adjust_for_ambient_noise(source, duration = 1) to calibrate the level to a good value. Alternatively, simply set this property to a high value initially (4000 works well), so the threshold is always above ambient noise levels: over time, it will be automatically decreased to account for ambient noise levels.
所以 Case By Case 耶?!


![L_{\Sigma }=10\log _{{10}}\!\left({\frac {{p_{1}}^{2}+{p_{2}}^{2}+\ldots +{p_{n}}^{2}}{{p_{0}}^{2}}}\right)\!~{\mathrm {dB}}=10\log _{{10}}\!\left[\left({\frac {p_{1}}{p_{0}}}\right)^{2}+\left({\frac {p_{2}}{p_{0}}}\right)^{2}+\ldots +\left({\frac {p_{n}}{p_{0}}}\right)^{2}\right]\!~{\mathrm {dB}}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/b2675e99b2d24d3ef00227217420bcbc906d38a5)



