『孫子算經』的作者不知何許人也,成書的年代不詳,一些學者根據書中事物發生的時間來看,約是在魏晉南北朝,距今已超過一千五百年了。
《卷下‧第三十一題》︰雞兔同籠問題的始祖
今有雉、兔同籠,上有三十五頭,下九十四足。問雉、兔各幾何?
答曰:雉二十三。兔一十二。
術曰:上置三十五頭,下置九十四足。半其足,得四十七。以少減多,再命之,上三除下三,上五除下五。下有一除上一,下有二除上二,即得。
又術曰:上置頭,下置足。半其足,以頭除足,以足除頭,即得。
《卷下‧第二十六題》︰中國餘數定理
今有物,不知其數。三、三數之,賸二;五、五數之,賸三;七、七數之,賸二。問物幾何?
答曰:二十三。
術曰:「三、三數之,賸二」,置一百四十;「五、五數之,賸三」,置六十三;「七、七數之,賸二」,置三十。并之,得二百三十三。以二百一十減之,即得。凡 三、三數之,賸一,則置七十;五,五數之,賸一,則置二十一;七、七數之,賸一,則置十五。一百六以上,以一百五減之,即得。
【孫子歌】
三人同行七十稀,
五樹梅花廿一枝,
七子團圓正半月,
除百零五便得知。
《孫子算經‧序》孫子曰:
夫算者,天地之經緯,群生之元首;五常之本末,陰陽之父母;星辰之建號,三光之表裹;五行之準平,四時之終始;萬物之祖宗,六藝之綱紀。稽群倫之聚散,考二氣之降升;推寒暑之迭運,步遠近之殊同;觀天道精微之兆基,察地理從橫之長短;采神祇之所在,極成敗之符驗;窮道德之 理,究性命之情。立規矩,準方圓,謹法度,約尺丈,立權衡,平重輕,剖毫釐,析黍絫;歷億載而不朽,施八極而無疆。散之不可勝究,斂之不盈掌握。嚮之者富 有餘,背之者貧且窶;心開者幼沖而即悟,意閉者皓首而難精。夫欲學之者必務量能揆己,志在所專。如是則焉有不成者哉。
南宋時的數學家秦九韶著作《數書九章》內有『大衍求一術』,正好用來『解詩』,『七十』除三餘一,卻為『五、七』整除;『二十一』除五餘一,卻為『三、七』整除;『十五』除七餘一,卻為『三、五』整除;三數的最小公倍數『三乘五乘七』是為『百零五』,所以答案是 ![]() 。『科技』與『人文』難道一定是『南轅北轍』不能『對話共歌』的嗎??
。『科技』與『人文』難道一定是『南轅北轍』不能『對話共歌』的嗎??
義大利的數學家朱塞佩‧皮亞諾 Giuseppe Peano 提出『自然數』之五條公設的系統。用著『未定義』的『基元』數『零 ![]() 』,以及『後繼數』successor 的概念,打造了一階算術系統,現今稱之為『皮亞諾算術系統』︰
』,以及『後繼數』successor 的概念,打造了一階算術系統,現今稱之為『皮亞諾算術系統』︰
一、 ![]() 是自然數。
是自然數。
二、 如果 ![]() 是自然數,則
是自然數,則 ![]() 的後繼數也是自然數。
的後繼數也是自然數。
三、 ![]() 不是任何自然數的後繼數。
不是任何自然數的後繼數。
四、 如果兩個自然數的後繼數相等,則這兩個自然數相等。
五、 任何關於自然數的命題,假使證明了這個命題對於自然數 ![]() 是真的,如果它對自然數
是真的,如果它對自然數 ![]() 為真時,又可以證明它對
為真時,又可以證明它對 ![]() 後繼數也真,那麼這個命題對所有的自然數都是真的── 數學歸納法 ──。
後繼數也真,那麼這個命題對所有的自然數都是真的── 數學歸納法 ──。
於是可以將皮亞諾算術表達成︰此處 ![]() 代表某數之後繼數
代表某數之後繼數
![]()
![]()
![]() ,就是數學歸納法
,就是數學歸納法
![]()
![]()
![]()
![]()
自從坎特爾用『集合論』將『數是什麼』以『一對一』『函數』來說明『有限集合』的『元素數目相等』概念之時,目的是通向『無限大』的『詮釋』,然而這使得人們重新發現『數ㄕㄨˇ數ㄕㄨˋ』的概念原來並非是『那麼簡單』。一八八九年皮亞諾所寫之《算術原理:用一種新方法的說明》 的書開啟了自然數公設化的先河。或許這就是邱奇之所以會用著『一一對應』的方式,創造了一種將整體『自然數』都給『編碼』encode 成了『 λ函式』的方法。在此為了避免『歷史事實』的爭議,就讓我們先拋掉所謂的『自然數』是不是該『始於一』之『歷史包袱』吧!也許簡單假設它是『起於無』的吧!由於『 λ 表達式』中根本就沒有『數』的『概念』,只有『變元』、『函式』和『應用』與可以『運用』,因此將『計物』比擬成『記點函式』應用於『所數之物』,彷彿用指點著它『一個一個』的數,『指點幾次』就是『該物之數』也是很自然的吧!!這樣我們就可以在『純 λ語言』裡『定義』邱奇數 ── 皮亞諾自然數的編碼 ──,是︰
一、 ![]() ,零
,零
二、 ![]() ,後繼數產生方法
,後繼數產生方法
三、 ![]() ,某數
,某數 ![]()
。假使你將『第一條』與『第二條』輸入設定為『純 λ 運算』且沒有『![]() 變換』的 Lambda Calculator,然後用著『逐次逐個』的方式定義『
變換』的 Lambda Calculator,然後用著『逐次逐個』的方式定義『![]() 』,你會得到︰
』,你會得到︰
0 [\f.\x.x] = \f.\x.x
1 [SUCC 0] = \f.\x.f x
2 [SUCC 1] = \f.\x.f (f x)
3 [SUCC 2] = \f.\x.f (f (f x))
4 [SUCC 3] = \f.\x.f (f (f [f x]))
5 [SUCC 4] = \f.\x.f (f (f [f (f x)]))
6 [SUCC 5] = \f.\x.f (f (f [f (f (f x))]))
7 [SUCC 6] = \f.\x.f (f (f [f (f (f {f x}))]))
8 [SUCC 7] = \f.\x.f (f (f [f (f (f {f (f x)}))]))
9 [SUCC 8] = \f.\x.f (f (f [f (f (f {f (f (f x))}))]))
…
假使將 ![]() 詮釋成的『作記號函式』── 在『物上作《 . 》記號』──, 這樣
詮釋成的『作記號函式』── 在『物上作《 . 》記號』──, 這樣 ![]() 就是調用『作記號函式』針對『當下物』
就是調用『作記號函式』針對『當下物』 ![]() 多作『一次』記號。由於這是『一一對應』的『記點』作法,那麼『物之數』自然就會『相等』於『做了幾次記號』的函式。難到這樣當真是『可行』的嗎?這一種『鏡花水月』的『定義』方式就已經能夠產生『算術』的了嗎??
多作『一次』記號。由於這是『一一對應』的『記點』作法,那麼『物之數』自然就會『相等』於『做了幾次記號』的函式。難到這樣當真是『可行』的嗎?這一種『鏡花水月』的『定義』方式就已經能夠產生『算術』的了嗎??
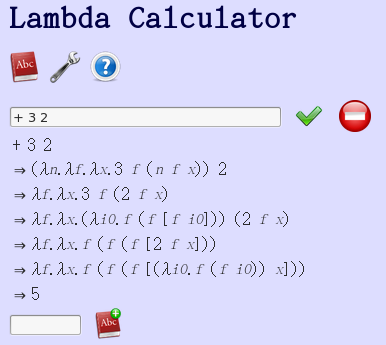
忘了誰說的︰檢驗是測試『真理』唯一的『辦法』。不如看看能否定義一個『計算之始』的簡單『加法』︰
+ [\m.\n.\f.\x.m f (n f x)] = \m.\n.\f.\x.m f (n f x)
─── 待續… λ 運算︰計物數《中》───