《百戰天龍》(MacGyver)(港譯《玉面飛龍》),美國電視劇系列,最初是在1985年9月在美國廣播公司電視網播出的,一直到1992年中的一季才結束,全劇共有七季139集。
故事舞台遍及世界各地,然而實際都是在加州南部(第一季、第二季和第七季)與加拿大的溫哥華周邊地區(第三季至第六季)拍攝 。雖然影集已經停播,但後來仍有兩部電視電影,分別是《馬蓋先奪寶奇謀[1](The Lost City of Atlantic)》和《馬蓋先橫掃千軍[2](Trail to Doomsday)》。影集及電影大致上的情節在於馬蓋先的冒險故事與化解危機。他從來不帶武器,只靠一把瑞士刀,他過人的智慧,利用身邊任何不起眼的物品來解決困難。馬蓋先有著廣泛的物理及化學知識,還有一切能實行他的「馬蓋先主義(MacGyverism)」的東西。
此處以平行光,思無窮,鑽籬木取離火!得百戰天龍智慧之旨耶☆物理固非數學,當物理原理用數學式子表達時,數學之正確,或需物理的詮釋乎?論疑惑生之所焉★
若問焦、焦面
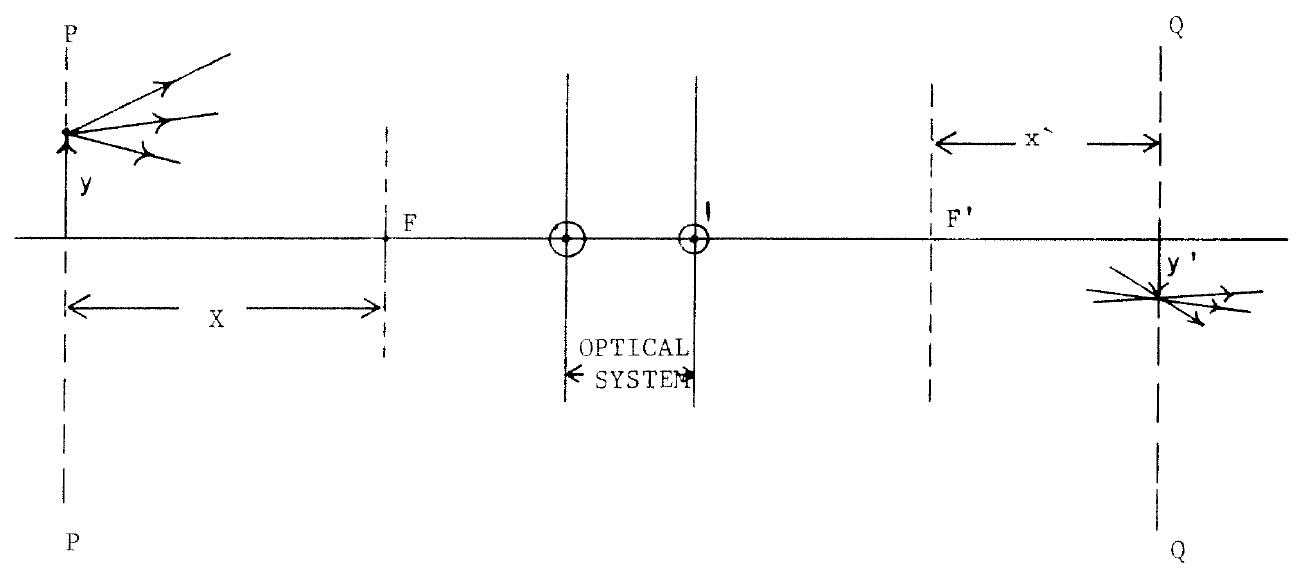
之成像法則
![]()
所 說何事?不管 ![]() 是正或是負,
是正或是負, ![]() 都是正的也!如是對凸透鏡來講,無窮遠之物
都是正的也!如是對凸透鏡來講,無窮遠之物 ![]() ,將成像於後焦點之平面上
,將成像於後焦點之平面上 ![]() 。那麼對凹透鏡來說,分明數學式子一樣!!又怎麼能一樣的呢??假使知道凹透鏡的後焦距面在凹透鏡之前,前焦距面在凹透鏡之後 ,能否釋疑呢???當真成像還是在後焦距面上!!!
。那麼對凹透鏡來說,分明數學式子一樣!!又怎麼能一樣的呢??假使知道凹透鏡的後焦距面在凹透鏡之前,前焦距面在凹透鏡之後 ,能否釋疑呢???當真成像還是在後焦距面上!!!
其實物理的基礎是現象事實,從幾何光學來談光行經透鏡時的現象 ,不過是光束之聚或散而已。事實與成不成像 ── 有人在看、相機在拍 ── 語意有差異矣。就像『照明』
Lighting
Lighting or illumination is the deliberate use of light to achieve a practical or aesthetic effect. Lighting includes the use of both artificial light sources like lamps and light fixtures, as well as natural illumination by capturing daylight. Daylighting (using windows, skylights, or light shelves) is sometimes used as the main source of light during daytime in buildings. This can save energy in place of using artificial lighting, which represents a major component of energy consumption in buildings. Proper lighting can enhance task performance, improve the appearance of an area, or have positive psychological effects on occupants.
Indoor lighting is usually accomplished using light fixtures, and is a key part of interior design. Lighting can also be an intrinsic component of landscape projects.
豈因為要成像嘛。而且見物攝影無非是見物之像而已。所以虛、實之名義,只是說︰透鏡後光線聚焦稱實像;若是透鏡後光線往前之延伸線才匯聚叫虛像的哩。
【實】
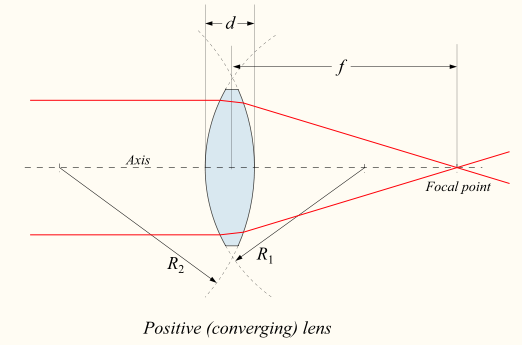

凸
【虛】
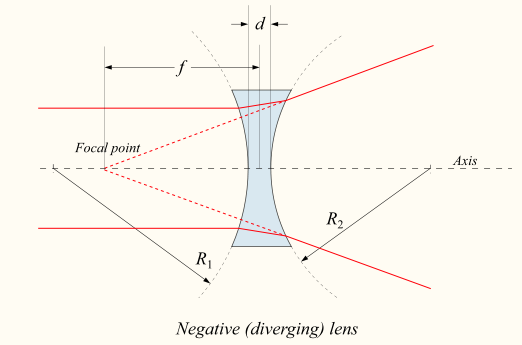

凹
所以『實點光源』、『虛點光源』不過『它』在哪裡的說法。物理現象『聚後實散』與『散前虛匯』,實際上是相同的吧。
因此一個一般光學矩陣
![]()
,可以等效於一個透鏡
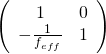
,在主平面參考系裡,享有著同樣的成像公式
![]()
又說什麼呢?設若以 ![]() 表示物距
表示物距 ![]() 比等效焦距大,但是很接近那個焦距。
比等效焦距大,但是很接近那個焦距。![]() 表達物距
表達物距 ![]() 比此等效焦距小,但是也很接近那個焦距。當此實、虛之際,聚、散之時
比此等效焦距小,但是也很接近那個焦距。當此實、虛之際,聚、散之時
![]()
![]()
到底該哪樣解釋
![]() 的啊??倘以現象而言,同也。皆平行光罷了!!
的啊??倘以現象而言,同也。皆平行光罷了!!
實 發光體 ![]() 自無窮遠處
自無窮遠處 ![]() 向凸透鏡之前焦距趨近,其像距
向凸透鏡之前焦距趨近,其像距 ![]() 將由後焦距往後遠離,當
將由後焦距往後遠離,當 ![]() ,像將在無窮遠也
,像將在無窮遠也 ![]() ,豈非透鏡後之平行光耶?★要是它從凸透鏡之主平面向後開始靠近前焦距面
,豈非透鏡後之平行光耶?★要是它從凸透鏡之主平面向後開始靠近前焦距面 ![]() ,那麼
,那麼 ![]() ,難到能不是以『所見』為重,省略其透鏡後已然平行的乎!☆
,難到能不是以『所見』為重,省略其透鏡後已然平行的乎!☆
試請讀者想想凹透鏡一致的乎★探探物貼 ![]() 凹凸鏡面上之理耶☆
凹凸鏡面上之理耶☆

─── 摘自《光的世界︰【□○閱讀】平行光之疑惑》
根據失傳之《平面國數典》記載︰
起初以『平投派』者為主流之學術圈,因著『人造點光源』的發明
,有人開始懷疑他們的『太陽』是『平行光源』之『假說』。這就開啟了『點投派』者的『理論』。史稱論戰前後縱貫數百年之久。終以『點投派』學者用『無窮遠』『投射點』函括了『平投派』之『平行線』告捷而終。
,作者與其苦惱該如何將『平面話』翻譯成『立體語』的呢?不如請讀者以事證事吧︰
Projection (mathematics)
In mathematics, a projection is a mapping of a set (or other mathematical structure) into a subset (or sub-structure), which is equal to its square for mapping composition (or, in other words, which is idempotent). The restriction to a subspace of a projection is also called a projection, even if the idempotence property is lost. An everyday example of a projection is the casting of shadows onto a plane (paper sheet). The projection of a point is its shadow on the paper sheet. The shadow of a point on the paper sheet is this point itself (idempotence). The shadow of a three-dimensional sphere is a closed disk. Originally, the notion of projection was introduced in Euclidean geometry to denote the projection of the Euclidean space of three dimensions onto a plane in it, like the shadow example. The two main projections of this kind are:
- The projection from a point onto a plane or central projection: If C is a point, called the center of projection, then the projection of a point P different from C onto a plane that does not contain C is the intersection of the line CP with the plane. The points P such that the line CP is parallel to the plane do not have any image by the projection, but one often says that they project to a point at infinity of the plane (see projective geometry for a formalization of this terminology). The projection of the point C itself is not defined.
- The projection parallel to a direction D, onto a plane or parallel projection: The image of a point P is the intersection with the plane of the line parallel to D passing through P. See Affine space § Projection for an accurate definition, generalized to any dimension.
The concept of projection in mathematics is a very old one, most likely having its roots in the phenomenon of the shadows cast by real world objects on the ground. This rudimentary idea was refined and abstracted, first in a geometric context and later in other branches of mathematics. Over time differing versions of the concept developed, but today, in a sufficiently abstract setting, we can unify these variations.
In cartography, a map projection is a map of a part of the surface of the Earth onto a plane, which, in some cases, but not always, is the restriction of a projection in the above meaning. The 3D projections are also at the basis of the theory of perspective.
The need for unifying the two kinds of projections and of defining the image by a central projection of any point different of the center of projection are at the origin of projective geometry. However, a projective transformation is a bijection of a projective space, a property not shared with the projections of this article.
Parallel projection
A parallel projection is a projection of an object in three-dimensional space onto a fixed plane, known as the projection plane or image plane, where the rays, known as lines of sight or projection lines, are parallel to each other. It is a basic tool in descriptive geometry. The projection is called orthographic if the rays are perpendicular (orthogonal) to the image plane, and oblique or skew if they are not.
Overview
A parallel projection is a particular case of projection in mathematics and graphical projection in technical drawing. Parallel projections can be seen as the limit of a central or perspective projection, in which the rays pass through a fixed point called the center or viewpoint, as this point is moved towards infinity. Put differently, a parallel projection corresponds to a perspective projection with an infinite focal length (the distance between the lens and the focal point in photography) or “zoom“. In parallel projections, lines that are parallel in three-dimensional space remain parallel in the two-dimensional projected image.
A perspective projection of an object is often considered more realistic than a parallel projection, since it more closely resembles human vision and photography. However, parallel projections are popular in technical applications, since the parallelism of an object’s lines and faces is preserved, and direct measurements can be taken from the image. Among parallel projections, orthographic projections are the most realistic, and are commonly used by engineers. On the other hand, certain types of oblique projections (for example cavalier projection, military projection) are very simple to implement, and are used to create quick and informal pictorials of objects.
The term parallel projection is used in the literature to describe both the procedure itself (a mathematical mapping function) as well as the resulting image produced by the procedure.
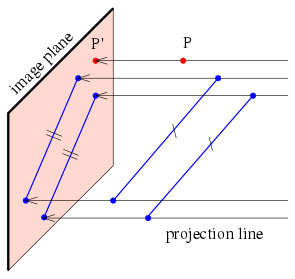
Parallel projection terminology and notations. The two blue parallel line segments to the right remain parallel when projected onto the image plane to the left.
且嘗試將『三維視線』投入『二維眼光』作一圖︰
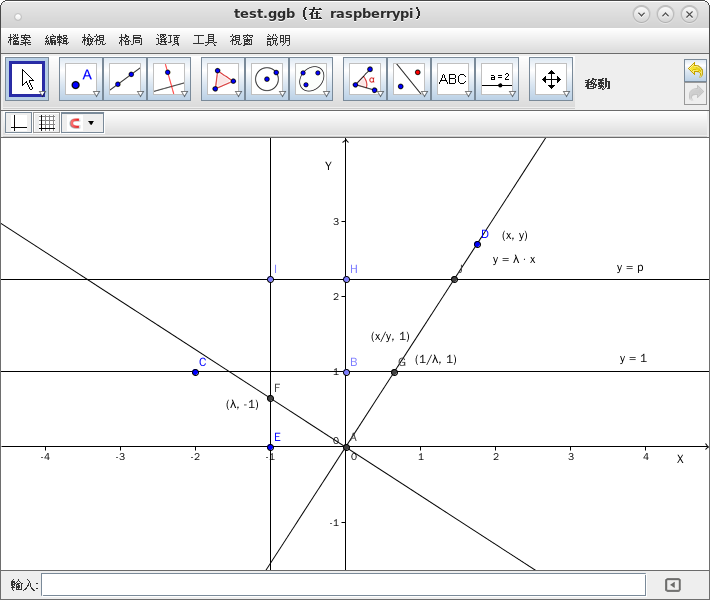
若說 ![]() 是『點投派』一『投影函數』,那麼
是『點投派』一『投影函數』,那麼
![]()
,依約一定落在『投影線』之 ![]() 點上。難到
點上。難到 ![]() 能夠『不等於』
能夠『不等於』 ![]() 乎?
乎?
如此豈不當然 ![]() 哩??
哩??
不過『平投派』能借『矩陣』表達『x 正投影』︰
![]()
符合『投影』約定『術語』︰ ![]()
怎能不問那 P 是否也『能用矩陣』表示耶◎