Euler’s Disk

Euler’s Disk is a scientific educational toy, used to illustrate and study the dynamic system of a spinning disk on a flat surface (such as a spinning coin), and has been the subject of a number of scientific papers.^[1] The apparatus is known for a seemingly paradoxical dramatic speed-up in spin rate as the disk loses energy and approaches a stopped condition. This phenomenon is named for Leonhard Euler, who studied it in the 18th century.

Computer rendering of Euler’s Disk on a slightly concave base

Components and use

The commercially available toy consists of a heavy, thick chrome-plated steel disk and a rigid, slightly concave, mirrored base. Included holographic magnetic stickers can be attached to the disk, to enhance the visual effect of “sprolling” or “spolling” (spinning/rolling), but these attachments are strictly decorative. The disk, when spun on a flat surface, exhibits a spinning/rolling motion, slowly progressing through different rates and types of motion before coming to rest—most notably, the precession rate of the disk’s axis of symmetry accelerates as the disk spins down. The rigid mirror is used to provide a suitable low-friction surface, with a slight concavity which keeps the spinning disk from “wandering” off a support surface.

An ordinary coin spun on a table, as with any disk spun on a relatively flat surface, exhibits essentially the same type of motion, but is normally more limited in the length of time before stopping. The commercially available Euler’s Disk toy provides a more effective demonstration of the phenomenon than more commonly found items, having an optimized aspect ratio and a precision polished, slightly rounded edge to maximize the spinning/rolling time.

Physics

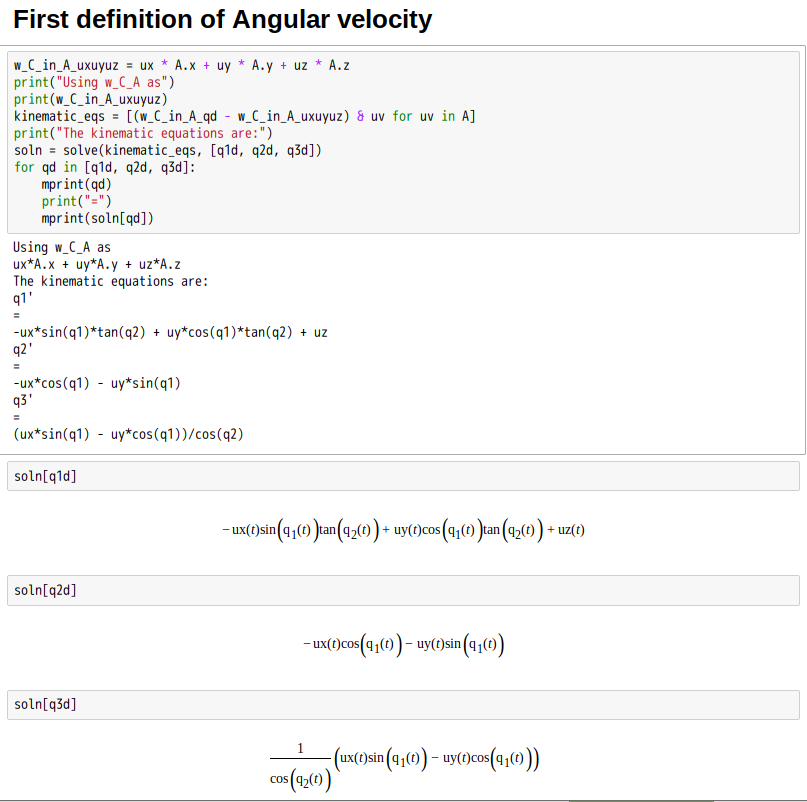
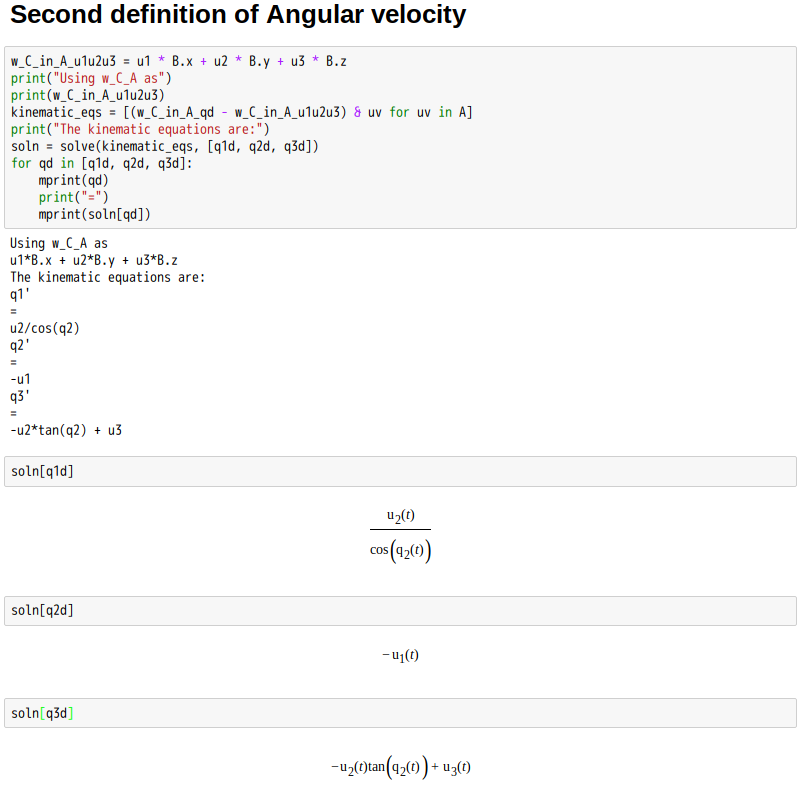
A spinning/rolling disk ultimately comes to rest, and it does so quite abruptly, the final stage of motion being accompanied by a whirring sound of rapidly increasing frequency. As the disk rolls, the point of rolling contact describes a circle that oscillates with a constant angular velocity $\displaystyle \omega$ . If the motion is non-dissipative (frictionless), $\displaystyle \omega$ is constant, and the motion persists forever; this is contrary to observation, since $\displaystyle \omega$ is not constant in real life situations. In fact, the precession rate of the axis of symmetry approaches a finite-time singularity modeled by a power law with exponent approximately −1/3 (depending on specific conditions).

There are two conspicuous dissipative effects: rolling friction when the coin slips along the surface, and air drag from the resistance of air. Experiments show that rolling friction is mainly responsible for the dissipation and behavior^[2]—experiments in a vacuum show that the absence of air affects behavior only slightly, while the behavior (precession rate) depends systematically on coefficient of friction. In the limit of small angle (i.e. immediately before the disk stops spinning), air drag (specifically, viscous dissipation) is the dominant factor, but prior to this end stage, rolling friction is the dominant effect.

故耳沐浴於相同的陽光裡、臥躺在一樣的青草間的人，畢竟好奇啊！想探索東西古今經驗之異同也！！

History of research

Moffatt

In the early 2000s, research was sparked by an article in the April 20, 2000 edition of Nature,^[3] where Keith Moffatt showed that viscous dissipation in the thin layer of air between the disk and the table would be sufficient to account for the observed abruptness of the settling process. He also showed that the motion concluded in a finite-time singularity. His first theoretical hypothesis was contradicted by subsequent research, which showed that rolling friction is actually the dominant factor.

Moffatt showed that, as time $\displaystyle t$ approaches a particular time $\displaystyle t_{0}$ (which is mathematically a constant of integration), the viscous dissipation approaches infinity. The singularity that this implies is not realized in practice, because the magnitude of the vertical acceleration cannot exceed the acceleration due to gravity (the disk loses contact with its support surface). Moffatt goes on to show that the theory breaks down at a time $\displaystyle \tau$ before the final settling time $\displaystyle t_{0}$ , given by:

$\displaystyle \tau \simeq \left[\left({\frac {2a}{9g}}\right)^{3}{\frac {2\pi \mu a}{M}}\right]^{\frac {1}{5}}$

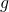where $\displaystyle a$ is the radius of the disk, $\displaystyle g$ is the acceleration due to Earth’s gravity, 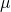$\displaystyle \mu$ the dynamic viscosity of air, and 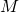$\displaystyle M$ the mass of the disk. For the commercially available Euler’s Disk toy (see link in “External links” below), 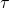$\displaystyle \tau$ is about 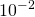$\displaystyle 10^{-2}$ seconds, at which time the angle between the coin and the surface, 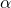$\displaystyle \alpha$ , is approximately 0.005 radians and the rolling angular velocity, 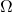$\displaystyle \Omega$ , is about 500 Hz.

Using the above notation, the total spinning/rolling time is:

$\displaystyle t_{0}={\frac {\alpha _{0}^{3}M}{2\pi \mu a}}$

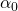where $\displaystyle \alpha _{0}$ is the initial inclination of the disk, measured in radians. Moffatt also showed that, if 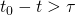$\displaystyle t_{0}-t>\tau$ , the finite-time singularity in 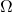$\displaystyle \Omega$ is given by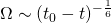

$\displaystyle \Omega \sim (t_{0}-t)^{-{\frac {1}{6}}}$

Experimental results

Moffatt’s theoretical work inspired several other workers to experimentally investigate the dissipative mechanism of a spinning/rolling disk, with results that partially contradicted his explanation. These experiments used spinning objects and surfaces of various geometries (disks and rings), with varying coefficients of friction, both in air and in a vacuum, and used instrumentation such as high speed photography to quantify the phenomenon.

In the 30 November 2000 issue of Nature, physicists Van den Engh, Nelson and Roach discuss experiments in which disks were spun in a vacuum.^[4] Van den Engh used a rijksdaalder, a Dutch coin, whose magnetic properties allowed it to be spun at a precisely determined rate. They found that slippage between the disk and the surface could account for observations, and the presence or absence of air only slightly affected the disk’s behavior. They pointed out that Moffatt’s theoretical analysis would predict a very long spin time for a disk in a vacuum, which was not observed.

Moffatt responded with a generalized theory that should allow experimental determination of which dissipation mechanism is dominant, and pointed out that the dominant dissipation mechanism would always be viscous dissipation in the limit of small $\displaystyle \alpha$ (i.e., just before the disk settles).^[5]

Later work at the University of Guelph by Petrie, Hunt and Gray^[6] showed that carrying out the experiments in a vacuum (pressure 0.1 pascal) did not significantly affect the energy dissipation rate. Petrie et al. also showed that the rates were largely unaffected by replacing the disk with a ring shape, and that the no-slip condition was satisfied for angles greater than 10°.

On several occasions during the 2007–2008 Writers Guild of America strike, talk show host Conan O’Brien would spin his wedding ring on his desk, trying to spin the ring for as long as possible. The quest to achieve longer and longer spin times led him to invite MITprofessor Peter Fisher onto the show to experiment with the problem. Spinning the ring in a vacuum had no identifiable effect, while a Teflon spinning support surface gave a record time of 51 seconds, corroborating the claim that rolling friction is the primary mechanism for kinetic energy dissipation.^{[citation needed]} Various kinds of rolling friction as primary mechanism for energy dissipation have been studied by Leine ^[7] who confirmed experimentally that the frictional resistance of the movement of the contact point over the rim of the disk is most likely the primary dissipation mechanism on a time-scale of seconds.

※ 參考

Finite-time singularity

The reciprocal function, exhibitinghyperbolic growth.

A finite-time singularity occurs when one input variable is time, and an output variable increases towards infinity at a finite time. These are important in kinematics and PDEs (Partial Differential Equations) – infinites do not occur physically, but the behavior near the singularity is often of interest. Mathematically the simplest finite-time singularities are power laws for various exponents, $\displaystyle x^{-\alpha },$ of which the simplest is hyperbolic growth, where the exponent is (negative) $\displaystyle x^{-1}.$ More precisely, in order to get a singularity at positive time as time advances (so the output grows to infinity), one instead uses $\displaystyle (t_{0}-t)^{-\alpha }$ (using t for time, reversing direction to $\displaystyle -t$ so time increases to infinity, and shifting the singularity forward from 0 to a fixed time $\displaystyle t_{0}$ ).

An example would be the bouncing motion of an inelastic ball on a plane. If idealized motion is considered, in which the same fraction of kinetic energy is lost on each bounce, the frequency of bounces becomes infinite as the ball comes to rest in a finite time. Other examples of finite-time singularities include the Painlevé paradox in various forms (for example, the tendency of a chalk to skip when dragged across a blackboard), and how the precession rate of a coin spun on a flat surface accelerates towards infinite, before abruptly stopping (as studied using the Euler’s Disk toy).

Hypothetical examples include Heinz von Foerster‘s facetious “Doomsday’s equation” (simplistic models yield infinite human population in finite time).

───

國立台中教育大學 NTCU

科學教育與應用學系

科學遊戲實驗室　　　回首頁

歐拉盤

一窺銅板滾動的奧秘

※器材：銅板、鐵環、反光板

※操作步驟與現象：

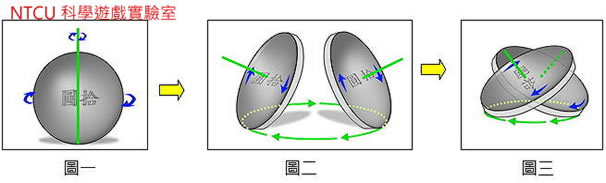
相信大家都玩過旋轉銅板的遊戲，銅板旋轉後到平躺靜止，還會發生很清晰的聲響。此種看似熟悉的現象，其實蘊含了相當為複雜的運動過程。

銅板一開始運動時，如圖一；銅板保持直立並且只有「自轉」（spin）：自轉軸通過銅板直徑並垂直於桌面，銅板與桌面的接觸點是固定的。直立自轉的速度變慢後，如圖二；銅板開始傾斜並包含了二種運動：(1)「滾動」（roll）運動：銅板邊緣沿著桌面滾動（如同車輪的滾動），且繞著圈圈滾動。(2)自轉運動，但是自轉軸與銅板表面垂直，並通過銅板中心（圖二綠色線段）。最後如圖三，銅板傾斜度增加，銅板與桌面撞擊產生的聲音頻率越來越快（但是自轉速度變慢），最後停止運動。

由於運動過程包括了自轉與滾動，因此常被稱為「sproll」運動；sproll一字取自：自轉spin的sp以及滾動roll的組合。