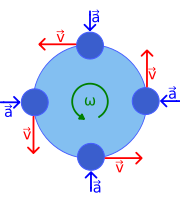
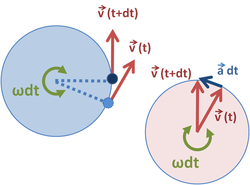
在物理學中,『圓周運動』是指物體的運動軌跡是個圓,或者沿著圓形路徑作運動。等速率圓周運動可以講是一種角速度 ![]() 不變的旋轉運動。分析後可得
不變的旋轉運動。分析後可得
![]()
![]()
![]()
![]()
其中 ![]() 是速度大小,
是速度大小,![]() 為加速度大小,
為加速度大小,![]() 是周期,
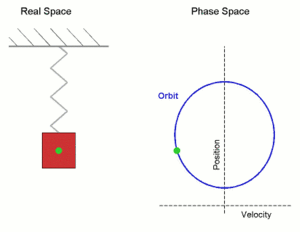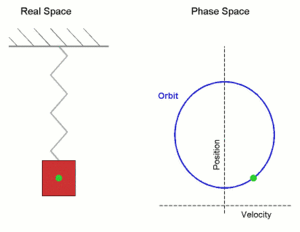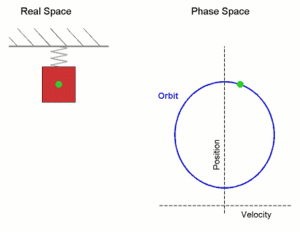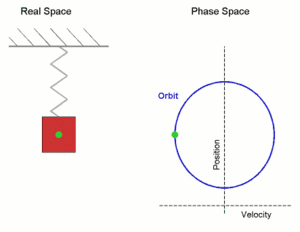
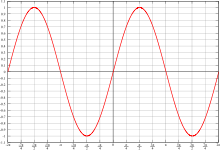
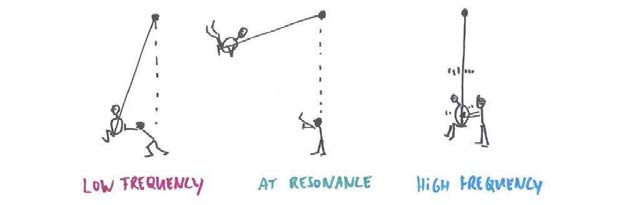
是周期,![]() 為角速度大小。假使有人說一個『簡諧運動』可以看成『圓周運動』,這是可以的嗎?據聞當年伽利略用望遠鏡觀測『木星』Jupiter 發現它周遭小星群的出沒有特定樣態, 由此斷定為『木星的月亮』,這件天文大事使得『地球』成了不是唯一有『月亮』的『行星』!從遠處看圓周運動就像是運動的軌跡『投影』,如果我們將一個圓周運動投影到
為角速度大小。假使有人說一個『簡諧運動』可以看成『圓周運動』,這是可以的嗎?據聞當年伽利略用望遠鏡觀測『木星』Jupiter 發現它周遭小星群的出沒有特定樣態, 由此斷定為『木星的月亮』,這件天文大事使得『地球』成了不是唯一有『月亮』的『行星』!從遠處看圓周運動就像是運動的軌跡『投影』,如果我們將一個圓周運動投影到 ![]() 軸上來看它的運動規律,可得
軸上來看它的運動規律,可得
![]() ,依據牛頓第二運動定律,
,依據牛頓第二運動定律,
![]()
![]()
![]()
,這難道不就是『虎克定律』![]() 的形式的嗎?對比後得到
的形式的嗎?對比後得到 ![]() 。無怪乎伽利略可以推測那是繞著木星作圓周運動的月亮,而勞侖茲會用『虎克弦』將『電子』與『原子核』栓綁起來,原來是可以這樣看的啊!!
。無怪乎伽利略可以推測那是繞著木星作圓周運動的月亮,而勞侖茲會用『虎克弦』將『電子』與『原子核』栓綁起來,原來是可以這樣看的啊!!
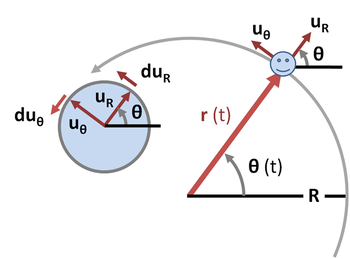
那麼可以用『圓周運動』 來描述『受驅振子』的嗎?一個半徑為 ![]() 的受軀均速圓周運動,就是講『質點』
的受軀均速圓周運動,就是講『質點』![]() 的振幅是
的振幅是 ![]() ,它所受到的『阻力』
,它所受到的『阻力』![]() 是在此圓的『切線』方向上。這樣『驅力』
是在此圓的『切線』方向上。這樣『驅力』![]() 可以分解成沿著圓的『切線方向』分量的
可以分解成沿著圓的『切線方向』分量的 ![]() 用以克服『阻力』
用以克服『阻力』![]() ,
,![]() ;『法線方向』的分量
;『法線方向』的分量 ![]() 或者『協同』或者『對抗』系統的虎克力。此時
或者『協同』或者『對抗』系統的虎克力。此時 ![]() ,依據牛頓第二運動定律,法線方向的『向心力』方程式為
,依據牛頓第二運動定律,法線方向的『向心力』方程式為 ![]() ,切線方向是
,切線方向是 ![]() ,假使將系統的『自然頻率』用
,假使將系統的『自然頻率』用 ![]() 來表示,化簡後得到
來表示,化簡後得到
![]() ,以及
,以及
![]()
圓周運動的思路,帶給我們另一種考察『受驅振子』系統行為的觀點。在此再次引用《【Sonic π】聲波之傳播原理︰振動篇》一文中的方程式
![]() 是驅動力的振幅大小。在線性微分方程式如
是驅動力的振幅大小。在線性微分方程式如 ![]() 的『求解』裡,如過『
的『求解』裡,如過『![]() 』是
』是 ![]() 的一個解,『
的一個解,『![]() 』是
』是 ![]() 一個『特解』,那麼『
一個『特解』,那麼『![]() 』就是該方程是的『通解』。我們已經知道
』就是該方程是的『通解』。我們已經知道 ![]() 的『低阻尼振子』之解在若干個弛豫時間後數值將變得太小了,所以它對於系統長時間之後的『行為』沒有太多的貢獻。因此我們說這個系統的『穩態解』steady-state solution 是
的『低阻尼振子』之解在若干個弛豫時間後數值將變得太小了,所以它對於系統長時間之後的『行為』沒有太多的貢獻。因此我們說這個系統的『穩態解』steady-state solution 是
![]() ,此處
,此處
![]()
是『響應阻抗』函數。而 ![]() 是驅動力引發的相位角,可由
是驅動力引發的相位角,可由
![]()
所決定,一般它表達著相位『遲滯』 lag 現象。
從圓周運動觀點來看,力的最『有效運用』只在於『克服阻力』,不論對抗或者協同『虎克力』,就是要改變系統的『自然振動』之頻率,因此『頻率偏離』愈大愈『多勞少功』。![]() 一式就是這個度量,它在
一式就是這個度量,它在 ![]() 時為『零』。試著幫一個『盪鞦韆』的小女孩『越盪越快』,就可以體驗這和『越盪越高』是很不相同的一回事 !!
時為『零』。試著幫一個『盪鞦韆』的小女孩『越盪越快』,就可以體驗這和『越盪越高』是很不相同的一回事 !!
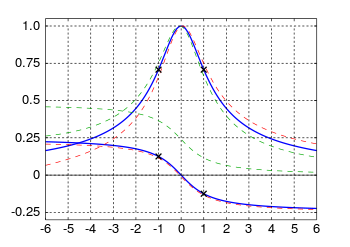
然而這個系統的最大振幅事實是發生在『共振頻率』 ![]() 時,這又是怎麼回事的呢?在物理上一個低阻尼『受驅振子』是用『無因次』的『品質因子』
時,這又是怎麼回事的呢?在物理上一個低阻尼『受驅振子』是用『無因次』的『品質因子』![]() 來描述『共振腔』 resonator 在鄰近『共振頻率』時,系統中能量比值,它的定義是
來描述『共振腔』 resonator 在鄰近『共振頻率』時,系統中能量比值,它的定義是
當信號振幅不隨著時間變化後,系統儲存能量和每個週期外界所提供能量的比例,此時系統儲存能量也不會隨時間變化:
![]()
此處『每周期能量損耗』Energy dissipated per cycle,就是『驅力』維持系統持續『振動』所需作的功。高 ![]() 的物理系統可以說是『振動能耗』小,並非所有的系統高
的物理系統可以說是『振動能耗』小,並非所有的系統高 ![]() 就一定好,通常它與『系統目的』性有關。比方講『 防止門突然關閉的阻尼器』它的
就一定好,通常它與『系統目的』性有關。比方講『 防止門突然關閉的阻尼器』它的 ![]() 因子為
因子為 ![]() ,然而計算機裡的『振盪器』需要頻率的高度穩定性
,然而計算機裡的『振盪器』需要頻率的高度穩定性 ![]() 因子可以高達
因子可以高達 ![]() 以上。
以上。
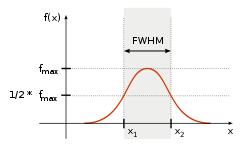
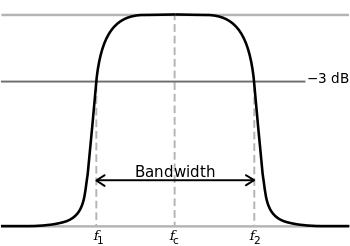
同時物理上也用著鄰近『共振時』,『振幅』的『半峰全寬』 FWHM Full width at half maximum 的『頻寬』 ![]() 來考察『共振效能』。對於高
來考察『共振效能』。對於高 ![]() 值的物理系統,很訝異的可以近似為
值的物理系統,很訝異的可以近似為 ![]() 。
。
從能量的觀點來看『受驅振子』的系統,假設 FWHM 遠小於 ![]() ,也就是說
,也就是說 ![]() ,因此
,因此
![]()
![]()
![]()
假使從能量的觀點來講,當 ![]() 時,這時系統能量為共振時的
時,這時系統能量為共振時的 ![]() 。於是
。於是 ![]() 。
。
此系統一周期儲存的能量是 ![]() ,一周期
,一周期 ![]() 『阻力』
『阻力』![]() 所作的功是
所作的功是
![]()
![]()
。所以 ![]() 。由於我們假設
。由於我們假設 ![]() ,於是我們就得到了
,於是我們就得到了
![]() 。
。
果真是『退一步,海闊天空』,『換個觀點』思考『大惑全解』 。自然中處處能有共振的現象,有些產生『壯觀奇景』,有些引發『毀滅災難』。人們所造之『橋』所建的『樓』,如果不細思與外界可能產生『共振』的問題,假使『橋垮樓塌』不該說是『天災』卻是『人禍』的啊??