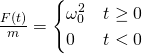來自於美國科羅拉多大學的 PhET Physics Education Technology 計劃,免費提供以樂趣、互動與研究為基礎的物理現象模擬軟體。這一個計畫是由二零零二年美國諾貝爾物理學獎得主之一的卡爾‧埃德溫‧威曼 Carl Edwin Wieman 所發起,根據 WiKi 上所載
began with Wieman’s vision to improve the way science is taught and learned. Their stated mission is “To advance science and math literacy and education worldwide through free interactive simulations.”
,按照現今官網的說明
PhET provides fun, interactive, research-based simulations of physical phenomena for free. We believe that our research-based approach- incorporating findings from prior research and our own testing- enables students to make connections between real-life phenomena and the underlying science, deepening their understanding and appreciation of the physical world.
…
目前它的線上內容早已經括及多類科學領域,並且很多內容也有了中文的翻譯網頁。作者認為如何用計算機輔助『教育』與『學習』正是今日當有之重要的『學習工具』,實現人們可以用『科學』來解釋『日常生活』中所經驗到的種種『自然現象』的教育宗旨。當你閱讀本文看到有『點擊啟動』的圖片時,請在『點擊啟動』的方形區域外,使用『滑鼠左鍵』點擊圖片的任何位置,進入嵌入式『PhET』線上模擬器的軟體世界。
一 個諧振子 harmonic oscillator 是一個物理系統,當它從平衡位置發生位移時,會受到一個正比於位移量 ![]() 的恢復力
的恢復力 ![]() ── 虎克定律──︰
── 虎克定律──︰![]() ,其中
,其中 ![]() 是一個正值常數。假使這個系統不受其它的外力影響,通常稱作『簡諧振子』Simple harmonic oscillator;如果此系統同時遭受到與速度成正比的『摩擦力』
是一個正值常數。假使這個系統不受其它的外力影響,通常稱作『簡諧振子』Simple harmonic oscillator;如果此系統同時遭受到與速度成正比的『摩擦力』 ![]() ,一般叫做『阻尼振子』Damped harmonic oscillator;要是這個系統還有著跟時間相關的外力
,一般叫做『阻尼振子』Damped harmonic oscillator;要是這個系統還有著跟時間相關的外力 ![]() 的作用,那麼就稱之為『受驅振子』Driven harmonic oscillators。
的作用,那麼就稱之為『受驅振子』Driven harmonic oscillators。
依據牛頓第二運動定律,一個簡諧振子的方程式為
![]() ,它的解是
,它的解是
![]() ,此處
,此處 ![]() 是『相位角』,
是『相位角』,
![]() ,式中
,式中 ![]() 是『角頻率』,
是『角頻率』,![]() 是『周期』。
是『周期』。
也就是說簡諧振子是一種『頻率』為 ![]() ,『振幅』為
,『振幅』為 ![]() 的週期運動。假設
的週期運動。假設 ![]() 的初始時,
的初始時,![]() ,得到
,得到
![]()
![]()
動能 = ![]() ,位能=
,位能=![]() ,系統總能量
,系統總能量
![]()
由此可以知道簡諧振子的系統總能量是一個常數,這稱之為『能量守恆量』定律,它和『振幅』的平方成正比。它的『頻率』![]() 只依賴於系統『固有』的
只依賴於系統『固有』的 ![]() 與
與 ![]() ,也是一個不變的常量。
,也是一個不變的常量。
依據牛頓第二運動定律,一個受驅振子的方程式為
![]() ,一般將之改寫為
,一般將之改寫為
![]() ,此處
,此處 ![]() 稱為『無阻尼』角頻率,而
稱為『無阻尼』角頻率,而 ![]() 叫做『阻尼比率』。如果『外力』
叫做『阻尼比率』。如果『外力』![]() ,那個方程式就成了『阻尼振子』的方程式
,那個方程式就成了『阻尼振子』的方程式
![]() ,當
,當 ![]() 它的解是
它的解是
![]() ,此處
,此處 ![]() 是相位角。
是相位角。
假使 ![]() 它的解是
它的解是
![]() 。
。
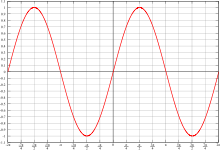
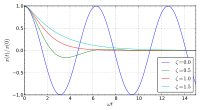
如果我們從 ![]() 的值來看『阻尼振子』的系統行為,當
的值來看『阻尼振子』的系統行為,當 ![]() 時,這一個系統已經『振動』不起來了,通常叫做『過阻尼』,負數的『指數項』使得系統的能量隨時間逐漸減少,
時,這一個系統已經『振動』不起來了,通常叫做『過阻尼』,負數的『指數項』使得系統的能量隨時間逐漸減少,![]() 的數值愈大能量減少將慢愈遲回到平衡。當
的數值愈大能量減少將慢愈遲回到平衡。當 ![]() 時,這一個系統也『振動』不起來了,通常稱之為『臨界阻尼』,此時系統會用最快的方式設法回到平衡,這個可是『關門』系統的『最佳解』!!。當
時,這一個系統也『振動』不起來了,通常稱之為『臨界阻尼』,此時系統會用最快的方式設法回到平衡,這個可是『關門』系統的『最佳解』!!。當 ![]() 時,這樣的諧振子系統稱作『低阻尼』,這時系統用著『低於無阻尼』的『頻率』振動,系統的『振幅』隨著時間以
時,這樣的諧振子系統稱作『低阻尼』,這時系統用著『低於無阻尼』的『頻率』振動,系統的『振幅』隨著時間以 ![]() 為比率逐漸減小以至於『不振動』為止。事實上從自然界中來的一般現象都會比『理論值』更快的到達『停止點』,就像說不只有『動摩擦力』與『靜摩擦力』之區分,摩擦力的『速度相關性』也不是這麼『簡單的正比』之假設,更別說理論上還有著『摩擦生熱』的問題必須要考慮。我們也許可以說為著追求『基本現象的理解』,通常都會『假設』了一些數學上『解答問題』的『理想條件』。
為比率逐漸減小以至於『不振動』為止。事實上從自然界中來的一般現象都會比『理論值』更快的到達『停止點』,就像說不只有『動摩擦力』與『靜摩擦力』之區分,摩擦力的『速度相關性』也不是這麼『簡單的正比』之假設,更別說理論上還有著『摩擦生熱』的問題必須要考慮。我們也許可以說為著追求『基本現象的理解』,通常都會『假設』了一些數學上『解答問題』的『理想條件』。
現在談談受外力影響下的受驅振子︰
它的解是
![]() ,此處相位角
,此處相位角 ![]() 由
由 ![]() 所決定。
所決定。
這個系統因為零點時刻突然受到固定大小的外力 ![]() 所驅動,震盪以
所驅動,震盪以 ![]() 為比率逐漸增大,一般用
為比率逐漸增大,一般用 ![]() 為時間尺度來衡量這個變化,每一
為時間尺度來衡量這個變化,每一 ![]() 單位時間,系統將以
單位時間,系統將以 ![]() 為比率改變振幅,在物理上稱之為『弛豫時間』Relaxation Time,工程上常用多的
為比率改變振幅,在物理上稱之為『弛豫時間』Relaxation Time,工程上常用多的 ![]() 單位時間,來談震盪達到預期大小的『安定時間』settling time。果真是『風吹枝擺』,待其風歇『搖曳而止』!!
單位時間,來談震盪達到預期大小的『安定時間』settling time。果真是『風吹枝擺』,待其風歇『搖曳而止』!!
![]() 是驅動力的振幅大小。在線性微分方程式如
是驅動力的振幅大小。在線性微分方程式如 ![]() 的『求解』裡,如過『
的『求解』裡,如過『![]() 』是
』是 ![]() 的一個解,『
的一個解,『![]() 』是
』是 ![]() 一個『特解』,那麼『
一個『特解』,那麼『![]() 』就是該方程是的『通解』。我們已經知道
』就是該方程是的『通解』。我們已經知道 ![]() 的『低阻尼振子』之解在若干個弛豫時間後數值將變得太小了,所以它對於系統長時間之後的『行為』沒有太多的貢獻。因此我們說這個系統的『穩態解』steady-state solution 是
的『低阻尼振子』之解在若干個弛豫時間後數值將變得太小了,所以它對於系統長時間之後的『行為』沒有太多的貢獻。因此我們說這個系統的『穩態解』steady-state solution 是
![]() ,此處
,此處
![]()
是『響應阻抗』函數。而 ![]() 是驅動力引發的相位角,可由
是驅動力引發的相位角,可由
![]()
所決定,一般它表達著相位『遲滯』 lag 現象。
物理上所說的『慣性』是指一個系統遭受外力時,它會發生『抵抗變化』的作為。這就是『響應阻抗』和『相位遲滯』的物理原由與命名由來。假使考察穩態解,我們是否可以講︰『原因 』── ![]() ── 產生成正比之『結果』──
── 產生成正比之『結果』── ![]() ── 的呢??
── 的呢??
─── 部落格訊息︰玩樹莓派, 自得其樂!!───