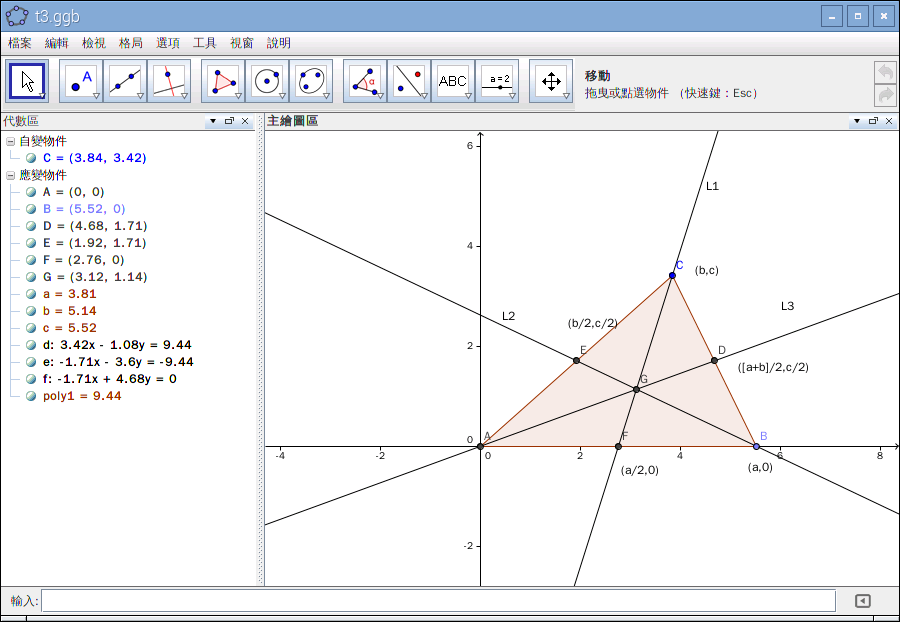
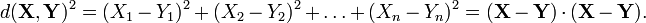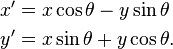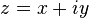部落格訊息

勇闖新世界︰ W!o《卡夫卡村》變形祭︰品味科學‧教具教材‧【專題】 PD‧箱子世界‧留白

若問為什麼平面上的一個一般三角形可以如下圖表示

 

三角形重心

 

，只用著 a \ , b \ , \ c 三個參數？即使在思考過 a 是『底』之『長』， c 是此『底』之『高』， b 是此『高』距與此『底』一端的距離。我們深信這就『確定』了那個三角形。然而若再問︰如果此三角形的三個頂點用更一般的 A \ (x_0, y_0)  、 B \ (x_1,y_1) 、 C \ (x_2,y_2) 來表達 ，如是分明有六個參數。那麼這兩種『表述』當真是一樣的嗎？設想你在桌面上『移動』一個三角形，從此『位置』此『方位』到達彼『位置』彼『方位』，你會認為這個三角形『改變』了嗎？？假使『直覺』以為『不變』，這個三角形就必得有使之『不變』的『因由』，這個『因由』不必『參照』解析幾何的『座標』而確立 。或可說它就是歐式幾何一個三角形的『定義』內涵而已。如此而言，一個『確定』的三角形，可由它的三個『邊長』來『確立』，所以六個參數補之以三個確定之邊長關係，豈非還是三個參數的耶？？

因為這個『歐式幾何』的『留白』，常使人懷疑『解析幾何』簡化『座標系』的『選擇』，到底『圖形』的『自由度』是幾何的了。說難道易，就請讀者思索︰平面上的『 □ 』與『 ○ 』，到底一方一圓需要幾個參數來描述的呢？

從物理上講，那個三角形就是『剛體』 rigid body ，它在『運動』中保持『形狀』的『不變性』。而且不同觀察者間的『座標變換』可以用

Rigid transformation

In mathematics, a rigid transformation (isometry) of a vector space preserves distances between every pair of points.[1][2] Rigid transformations of the plane R2, space R3, or real n-dimensional space Rn are termed a Euclidean transformation because they form the basis of Euclidean geometry.[3]

The rigid transformations include rotations, translations, reflections, or their combination. Sometimes reflections are excluded from the definition of a rigid transformation by imposing that the transformation also preserve the handedness of figures in the Euclidean space (a reflection would not preserve handedness; for instance, it would transform a left hand into a right hand). To avoid ambiguity, this smaller class of transformations is known as proper rigid transformations (informally, also known as roto-translations). In general, any proper rigid transformation can be decomposed as a rotation followed by a translation, while any rigid transformation can be decomposed as an improper rotation followed by a translation (or as a sequence of reflections).

Any object will keep the same shape and size after a proper rigid transformation.

All rigid transformations are examples of affine transformations. The set of all (proper and improper) rigid transformations is a group called the Euclidean group, denoted E(n) for n-dimensional Euclidean spaces. The set of proper rigid transformation is called special Euclidean group, denoted SE(n).

In kinematics, proper rigid transformations in a 3-dimensional Euclidean space, denoted SE(3), are used to represent the linear and angular displacement of rigid bodies. According to Chasles’ theorem, every rigid transformation can be expressed as a screw displacement.

Formal definition

A rigid transformation is formally defined as a transformation that, when acting on any vector v, produces a transformed vector T(v) of the form

T(v) = R v + t

where RT = R−1 (i.e., R is an orthogonal transformation), and t is a vector giving the translation of the origin.

A proper rigid transformation has, in addition,

det(R) = 1

which means that R does not produce a reflection, and hence it represents a rotation (an orientation-preserving orthogonal transformation). Indeed, when an orthogonal transformation matrix produces a reflection, its determinant is –1.

Distance formula

A measure of distance between points, or metric, is needed in order to confirm that a transformation is rigid. The Euclidean distance formula for Rn is the generalization of the Pythagorean theorem. The formula gives the distance squared between two points X and Y as the sum of the squares of the distances along the coordinate axes, that is

d(\mathbf{X},\mathbf{Y})^2 = (X_1-Y_1)^2 + (X_2-Y_2)^2 + \ldots + (X_n-Y_n)^2 = (\mathbf{X}-\mathbf{Y})\cdot(\mathbf{X}-\mathbf{Y}).

where X=(X1, X2, …, Xn) and Y=(Y1, Y2, …, Yn), and the dot denotes the scalar product.

Using this distance formula, a rigid transformation g:Rn→Rn has the property,

d(g(\mathbf{X}), g(\mathbf{Y}))^2 = d(\mathbf{X}, \mathbf{Y})^2.

───

 

來作轉換的矣！！

如是細思二維空間上的『旋轉』︰

Two dimensions

In two dimensions, to carry out a rotation using matrices the point (x, y) to be rotated (orientation from positive x to y) is written as a vector, then multiplied by a matrix calculated from the angle, θ:

\begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}.

where (x′, y′) are the coordinates of the point that after rotation, and the formulae for x′ and y′ can be seen to be

The vectors \begin{bmatrix} x \\ y \end{bmatrix} and \begin{bmatrix} x' \\ y' \end{bmatrix} have the same magnitude and are separated by an angle θ as expected.

Points on the R2 plane can be also presented as complex numbers: the point (x, y) in the plane is represented by the complex number

z = x + iy

This can be rotated through an angle θ by multiplying it by eiθ, then expanding the product using Euler’s formula as follows:

and equating real and imaginary parts gives the same result as a two-dimensional matrix:

Since complex numbers form a commutative ring, vector rotations in two dimensions are commutative, unlike in higher dimensions. They have only one degree of freedom, as such rotations are entirely determined by the angle of rotation.[1]

───

 

那一方一圓問題的答案，是否不言而喻的哩？？！！