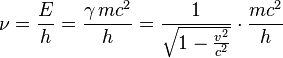樹莓派、樹莓派之學習、樹莓派之教育

W!o+ 的《小伶鼬工坊演義》︰神經網絡【FFT】八

自從愛因斯坦用『光子』 ── 頻率為 \nu 之光量子，攜帶 h \nu 的能量 ── 來解釋『光電效應』，就開啟了『光』之『波‧粒二重性』。其後德布羅意設想

物質波

物理學中，物質波（即德布羅意波）係指所有物質的波（見波粒二象性）。

德布羅意說明了波長和動量成反比；頻率和總能成正比 之關係，是路易·德布羅意於1923年在他的博士論文提出的。

第一德布羅意方程式指出，粒子波長λ（亦稱德布羅意波長）和動量p的關係：（下式中普朗克常數h、粒子靜質量m、粒子速度v、勞侖茲因子γ和真空光速c）

\lambda = \frac{h}{p} = \frac{h}{\gamma mv} = \frac{h}{mv} \sqrt{1 - \frac{v^2}{c^2} }

第二德布羅意方程式指出頻率ν和總能E的關係：

\nu = \frac{E}{h} = \frac{\gamma\,mc^2}{h} = \frac {1}{\sqrt{1 - \frac{v^2}{c^2}}} \cdot \frac{mc^2}{h}

這兩個式子通常寫作

p = {h \over \lambda} = \hbar {2\pi \over \lambda} = \hbar k \,
E = h \nu = \hbar \cdot 2\pi \nu = \hbar \omega \,

 

200px-Propagation_of_a_de_broglie_plane_wave.svg

平面波

 

200px-Propagation_of_a_de_broglie_wavepacket.svg

波包
德布羅意波的1維傳播，複值波幅的實部以藍色表示、虛部以綠色表示。在某位置找到粒子的機率（以顏色的不透明度表示）呈波形狀延展。

───

 

說明『物質』具有『波動性』也自然順理成章。雖說

波包

在任意時刻，波包（wave packet）是局限在空間的某有限範圍區域內的波動，在其它區域的部分非常微小，可以被忽略。波包整體隨著時間流易移動於空間。波包可以分解為一組不同頻率、波數、相位、波幅的正弦波，也可以從同樣一組正弦波構成；在任意時刻，這些正弦波只會在空間的某有限範圍區域相長干涉，在其它區域會破壞性干涉。[1]:53-56[2]:312-313描繪波包輪廓的曲線稱為包絡線。依據不同的演化方程式，在傳播的時候，波包的包絡線（描繪波包輪廓的曲線）可能會保持不變（沒有色散），或者包絡線會改變（有色散）。

在量子力學裏，波包可以用來代表粒子，表示粒子的機率波；也就是說，表現於位置空間，波包在某時間、位置的波幅平方，就是找到粒子在那時間、位置的機率密度；在任意區域內，波包所囊括面積的絕對值平方，就是找到粒子處於那區域的機率。粒子的波包越狹窄，則粒子位置的不確定性越小，而動量的不確定性越大；反之亦然。這位置的不確定性和動量的不確定性，兩者之間無可避免的關係，是不確定性原理的一個標準案例。[1]:53-56

描述粒子的波包滿足薛丁格方程式，是薛丁格方程式的數學解。通過含時薛丁格方程式，可以預測粒子隨著時間演化的量子行為。這與在經典力學裏的哈密頓表述很類似。[3]:123

200px-Wave_packet.svg

實線是波包，虛線是波包的包絡。當波包傳播於空間時，包絡以群速度移動。

───

 

的物理性質早為人所熟知。但講起『小波分析』卻是新鮮之事︰

小波分析

小波分析（wavelet analysis）或小波轉換（wavelet transform）是指用有限長或快速衰減的、稱為母小波（mother wavelet）的振盪波形來表示訊號。該波形被縮放和平移以匹配輸入的訊號。

小波一詞由Morlet和Grossman在1980年代早期提出。他們用的是法語詞ondelette – 意思就是”小波”。後來在英語裡，”onde”被改為”wave”而成了wavelet。

小波變換分成兩個大類：離散小波變換（DWT） 和連續小波轉換（CWT）。兩者的主要區別在於，連續變換在所有可能的縮放和平移上操作，而離散變換採用所有縮放和平移值的特定子集。

小波理論和幾個其他課題相關。所有小波變換可以視為時域頻域表示的形式，所以和調和分析相關。所有實際有用的離散小波變換使用包含有限脈衝響應濾波器的濾波器段（filter band）。構成CWT的小波受海森堡的測不準原理制約，或者說，離散小波基可以在測不準原理的其他形式的情境中考慮。

母小波

簡單來說（技術上並非如此），母小波函數\psi\ (t)必須滿足下列條件：

\int_{-\infty}^{\infty} |\psi (t)|\ ^2\, dt = 1,也即\psi\in L^2(\R)並單位化
\int_{-\infty}^{\infty} |\psi\ (t)|\, dt <\infty,也即\psi\in L^1(\R)
\int_{-\infty}^{\infty} \psi\ (t)\, dt = 0

多數情況下，需要要求\psi連續且有一個矩(moment)為0的大整數M，也即對所有整數m<M滿足

\int_{-\infty}^{\infty} t^m\,\psi\ (t)\, dt = 0

即母小波有M個消失矩(vanishing moment)，且M不等於0，這表示母小波必須不是常數且均值為0。

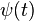\int_{-\infty}^{\infty} \frac{|\overset{\frown}{\psi} (\omega)|^{2}}{|\omega|} d\omega <\infty\ \ ，稱作可採納性(admissibility condition)，其中\overset{\frown}{\psi}(\omega)是 \psi(t)的傅立葉轉換。

技術上來講，母小波必須滿足可採納性條件以使某個解析度的恆等成立。

根據Morlet的原始形式，母小波定義為

\psi _{a,b} (t) = {1 \over {\sqrt a }}\psi \left( {{{t - b} \over a}} \right)

其中a是縮放因子，當|a|<1時，母小波被壓縮，在時間軸上有較小的支撐度，並且對應到高頻，因為母小波變窄、變化變快， 反之，當|a|>1時，母小波變寬、變化較慢，所以對應到低頻。b則是平移參數，用來決定母小波的位置。

根據訊號處理的測不準原理:

\Delta t \Delta \omega \geqq \frac{1}{2}

t 是時間，ω是角頻率(ω = 2πf，f是順時頻率)。

當時間解析度較高時，頻率解析度就會下降，反之，頻率解析度高時，時間解析度下降。當母小波或窗函數取的越寬，\Delta t的值越大。

當\Delta t越大:

1. 縮放因子越大，對應低頻。
2. 頻率解析度高。
3. 時間解析度低。

當\Delta t越小:

1. 縮放因子越小，對應高頻。
2. 頻率解析度低。
3. 時間解析度高。

雖然跟短時距傅立葉轉換一 樣能同時分析時間和頻率，但是小波轉換在高頻的時間解析度較好，在低頻時則是頻率解析度較好， 剛好符合我們對訊號分析在高低頻的解析度要求，因為在低頻時，例如頻率從1Hz變到2Hz，頻率差了一倍，所以頻率的變化相較時間的變化是比較明顯且重要 的，然而在高頻時，例如頻率從1000Hz變到1001Hz，頻率相較時間的變化不大，所以對時間解析度的要求較高。但是短時距傅立葉轉換的解析度並不會隨著頻率而變化，下圖顯示兩者解析度變化的比較:

STFT and WT.jpg

母小波的一些例子：

 

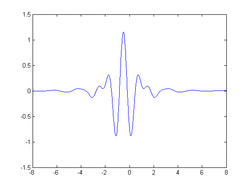
Wavelet_-_Meyer

Meyer

 

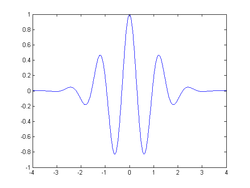
250px-Wavelet_-_Morlet

Morlet

 

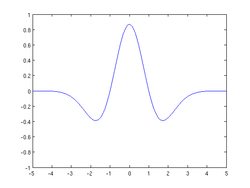
Wavelet_-_Mex_Hat

墨西哥帽

 

……

和傅里葉變換比較

小波變換經常和傅里葉變換做比較，在後者中訊號用正弦函數的和來表示。

 
轉換形式 數學式 參數
傅立葉變換 X(f) = \int_{-\infty}^{\infty} x(t)e^{-j2 \pi ft}\, dt f, 頻率
短時距傅立葉變換 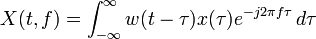X(t, f) = \int_{-\infty}^{\infty} w(t-\tau)x(\tau) e^{-j 2 \pi f \tau} \, d\tau t, 時間; f, 頻率
小波轉換 X(a,b) = \frac{1}{\sqrt{b}}\int_{-\infty}^{\infty}\ x(t){\Psi\left(\frac{t - a}{b}\right)} \, dt a, 時間; b, 尺度

標準的傅立葉變換將訊號從時域轉換到頻率域上做分析，但沒辦法從頻率域上得知訊號在不同時間的頻率資訊，只能知道該訊號包含哪些頻率成份，因此不適合用來分析一個頻率會隨著時間而改變的訊號，例如:音樂訊號。

然而短時距傅立葉變換（Short-time Fourier transform）（STFT）比傅立葉變換多了一個窗函數(window function)，可以分析出隨著時間變化的頻率,隨著窗函數大小的不同會有不同的頻率和時間解析度，以方形窗函數為例，當窗函數寬度越大，頻率的解析度越好，但時間解析度下降，反之，當窗函數寬度越小，時間的解析度越好，頻率解析度下降，然而有限長度的窗函數大小會限制頻率解析度，不過小波轉換能解決這個問題，通過多解析度分析通常可以給出更好的訊號表示。

另外，當輸入訊號為二維時(例如:影像)，短時距傅立葉變換的輸出為四維度，但小波轉換仍是二維訊號，所以在影像處理上通常會使用小波轉換而非短時距傅立葉變換。

小波變換的計算複雜度也更小，只需要\mathcal{O}(N)時間，快於快速傅里葉變換的\mathcal{O}(N \log N)，其中N代表數據大小。

 

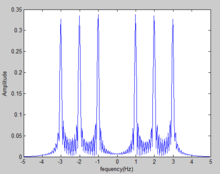
Fourier_transform

傅立葉轉換

 

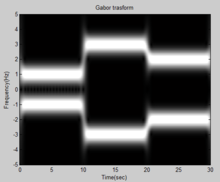
Gabor_transform

STFT

 

可否藉此理解人耳之奧妙以及神奇的耶！！？？

音樂訊號分析

小波轉換亦可用在音樂訊號上，像是樂器自動辨識的應用，第一種為先使用一維小波轉換將聲音訊號分解為不同頻率範圍的各個頻帶，接著再對各個頻帶中擷 取能量平均值以及能量標準差視為一維小波轉換之特徵向量。而第二種方法為先將聲音訊號轉成頻譜圖並視為一張二維影像，對此頻譜圖做二維小波轉換分解出各個 頻帶，再對頻帶中擷取能量平均值和能量標準差做為二維小波的特徵向量。最後，利用相鄰近似法使用歐基里德距離來計算測試資料的特徵向量和每一樂器的特徵向 量之距離，並取最小距離為辨識結果的樂器類別[3]。

而小波轉換也常用在音樂訊號的壓縮，由於人耳對聲音各頻帶是有其感知力的，故有些頻帶人無法聽見，有些頻帶人耳特別靈敏。利用離散小波轉換來將音樂 訊號做高低頻切割多次，就可以將原訊號分成許多子頻帶(sub-band)，但傳統離散小波轉換計算架構，將波型分成高頻與低頻後，下一次的切割只對低頻 做切割，故沒辦法完全分割出與人耳感知頻帶相符合的子頻帶。於是更精細的計算架構被提出，稱為離散小波包轉換(discrete wavelet packet transform)，原理就是音樂訊號被分成高頻訊號後，會再做分割。一段音樂訊號就可以被分割成更貼近人耳25個頻帶的訊號，這樣的分割法更優於一般 傅立葉分析所使用的濾波器，從這些子頻帶中，找出能夠被屏蔽的訊號，濾除之後，就可以將原本音樂訊號檔案大小壓縮了。

在辨識音樂訊號的樂譜上也有其應用，音樂訊號由一個個音符組成，而每個音符以特定的節奏出現，通常是成群的諧音出現，若要分辨出一段訊號最主要的頻 率為何，必須濾除其泛音才能判斷，而由離散小波轉換的多重解析度分割就可以將泛音區隔在不同的子頻帶中，而且訊號中的雜訊也可以依同樣方法被濾除。由於是 要偵測transient 現象，基於要偵測什麼樣的訊號就使用跟它很像的訊號當作基底拆解它這個原則，故在選擇小波基底時，就要選擇較有突然劇烈變化的母小波，如此一來小波轉換後 的小波係數，能量就會聚集在原訊號有劇烈變化之處了[4]，由此方法可有效辨識音樂訊號的音高(也就是頻率)。

───