樹莓派、樹莓派之學習、樹莓派之教育

W!o+ 的《小伶鼬工坊演義》︰神經網絡【backpropagation】五

人能否從歷史人物身上學習什麼呢？比方說維基百科『高斯』詞條如是紀載︰

約翰·卡爾·弗里德里希·高斯（德語：Johann Karl Friedrich Gauß關於這個音頻文件  （說明·

      1. 資訊
）；英語：Gauss；拉丁語：Carolus Fridericus Gauss；1777年4月30日－1855年2月23日）， 德國著名數學家、物理學家、天文學家、大地測量學家，生於布倫瑞克，卒於哥廷根 。高斯被認為是歷史上最重要的數學家之一[1]，並有「數學王子」的美譽[2]。

1792年，15歲的高斯進入Collegium Carolinum，現今的布倫瑞克科技大學（Braunschweig University of Technology）。在那裡，高斯開始對高等數學作研究。獨立發現了二項式定理的一般形式、數論上的「二次互反律」、質數定理、及算術-幾何平均數。[3]

1795年高斯進入哥廷根大學。1796年，19歲的高斯得到了一個數學史上極重要的結果，就是《正十七邊形尺規作圖之理論與方法》。

1855年2月23日清晨，77歲的高斯在格於丁根天文台的躺椅上睡覺時去世。[4]

Bendixen_-_Carl_Friedrich_Gauß,_1828

1838年出版的天文學通報中高斯肖像。

生平

高斯是一對普通夫婦的兒子。他的母親是一個貧窮石匠的女兒，雖然十分聰明，但卻沒有接受過教育，近似於文盲。在她成為高斯父親的第二個妻子之前，她從事女傭工作。他的父親曾做過工頭，商人的助手和一個小保險公司的評估師。高斯三歲時便能夠糾正他父親的借債帳目的事情，已經成為一個軼事流傳至今。他曾說，他能夠在腦袋中進行複雜的計算。他的職業是園丁，他做事認真。

高斯10歲時利用很短的時間就計算出了小學老師提出的問題：自然數從1到100的求和。他所使用的方法是：對50對構造成和101的數列求和（1＋100，2＋99，3＋98……），同時得到結果：5050。

───

 

這位一代之數學天才有著非凡的洞察力！能用不俗的觀點處理數學計算問題！！傳聞所說的老師之刁難︰計算

1+2+3+ \cdots + 99 +100

，終因『巧妙』之法而迅速落幕也︰

Sum = 1+2+3+ \cdots + 99 +100

Sum = 100+99+ \cdots +3+2 +1

2 \cdot Sum = (1+100) + (2+99) + \cdots + (99+2) + (100+1)

= (101) \times 100

\therefore Sum = \frac{101 \times 100}{2} = 5050

 

但是此『巧妙』之法難以『推廣』，舉例說︰計算

1^2 + 2^2 + 3^2 + \cdots + {99}^2 +{100}^2

無法運作此法也？？！！難道還有更『一般性』的法子嗎？？假使設想一個『序列』 S_n = n^2 ，可知 S_{n+1} - S_n = {(n+1)}^2 - n^2 = 2 \cdot n +1 ，因此

S_2 - S_1 = 2 \cdot 1 +1

S_3 - S_2 = 2 \cdot 2 +1

……

S_n - S_{n-1} = 2 \cdot (n-1) + 1

S_{n+1} - S_n = 2 \cdot n +1

\therefore S_{n+1} - S_1 = 2 \cdot (1+2+ \cdots + (n-1) + n) + n

所以

1+2+ \cdots + (n-1) + n = \frac{S_{n+1} - S_1 - n}{2} = \frac{n \cdot (n+1)} {2}

 

要是依樣畫葫蘆構造『序列』 C_n = n^3 ， 那麼 C_{n+1} - C_n = {(n+1)}^3 - n^3 = 3 \cdot n^2 + 3 \cdot n + 1 ，故而

C_2 - C_1 = 3 \cdot 1^2 + 3 \cdot 1 +1

C_3 - C_2 = 3 \cdot 2^2 + 3 \cdot 2 +1

……

C_n - C_{n-1} = 3 \cdot {(n-1)}^2 + 3 \cdot (n-1) +1

C_{n+1} - C_n = 3 \cdot n^2 + 3 \cdot n +1

\therefore C_{n+1} - C_1 = 3 \cdot (1^2 + 2^2 + \cdots + n^2) + 3 \cdot (1+2+ \cdots +n) + n

於是

1^2 + 2^2 + \cdots + n^2 = \frac{C_{n+1} - C_1 - 3 \cdot (1+2+ \cdots +n) - n}{3} = \frac{n \cdot (n+1) \cdot (2 \cdot n +1)}{6}

 

果真可以『類推』耶！！？？反之我們曉得 1^2 + 2^2 + \cdots + n^2 必為整數，因此 n \cdot (n+1) \cdot (2 \cdot n +1) 必是六的倍數，但將要如何證明的呢？？？故知方法有窮而無盡！應用無窮實難盡！！終究運作之道祇存乎一心矣！！！

作者之所以寫這一段前言，是想說明『反向傳播演算法』不外乎是依據『定義』

\delta^l_j \equiv \frac{\partial C}{\partial z^l_j}. \ \ \ \ (29)

，使用『鏈式法則』有『目的』之『推導』罷了？？

tikz21

 

如能清清楚楚了解此『目的』，『推導』方向的『選擇』也就明明白白，不欲做『多餘之計算』也！從『已知』推向『未知』的呀 ！！

層與層之間有關係

{\vec z}^{\ l} \ \equiv \ W^{\ l} \ {\vec a}^{\ l-1} \ + \ {\vec b}^{\ l}

可以『向前瞧』或『向後看』，既然名之為『反向』欲『向後看』也。為什麼的呢？因為我們僅知『最終誤差』是

C = \frac{1}{2n} \sum_x \|y(x)-a^L(x)\|^2, \ \ \ \ (26)

，我們想透過改變『之前』的『權重』W^{\ l}  和『基底』 {\vec b} ^l 來『減少』此『誤差』，『向後看』才能知道將改變多少的乎！！

因此當 Michael Nielsen 先生證明式子 BP2 時，首先明示此『目的』

Next, we’ll prove (BP2), which gives an equation for the error \delta^l in terms of the error in the next layer, \delta^{l+1}. To do this, we want to rewrite \delta^l_j = \partial C / \partial z^l_j in terms of \delta^{l+1}_k = \partial C / \partial z^{l+1}_k. We can do this using the chain rule,

\delta^l_j & = & \frac{\partial C}{\partial z^l_j} \tag{40}\\ & = & \sum_k \frac{\partial C}{\partial z^{l+1}_k} \frac{\partial z^{l+1}_k}{\partial z^l_j} \tag{41}\\ & = & \sum_k \frac{\partial z^{l+1}_k}{\partial z^l_j} \delta^{l+1}_k, \ \ \ \ (40 - 42)
───

 

，實是畫龍點睛之筆法也。

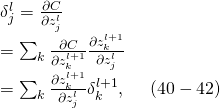
由於 BP3 、BP4 兩式之證明給當成了『習題』，此處就算『題解』的吧。為方便閱讀，列出相干關係函式如下︰

C = C({\vec a}^L)

{\vec a}^L = \sigma ({\vec z}^L)

\sigma(z) \equiv \frac{1}{1+e^{-z}}

{\vec z}^{\ l} \ \equiv \ W^{\ l} \ {\vec a}^{\ l-1} \ + \ {\vec b}^{\ l}

\delta^l_j \equiv \frac{\partial C}{\partial z^l_j}. \ \ \ \ (29)

 

【BP3】

\frac{\partial C}{\partial b^l_j} = \frac{\partial C}{\partial z^l_j} \cdot \frac{\partial z^l_j}{\partial b^l_j} = \delta^l_j \cdot 1 = \delta^l_j

 

【BP4】

\frac{\partial C}{\partial w^l_{jk}} = \frac{\partial C}{\partial z^l_j} \cdot \frac{\partial z^l_j}{\partial w^l_{jk}} = \delta^l_j \cdot a^{l-1}_k = a^{l-1}_k \cdot \delta^l_j