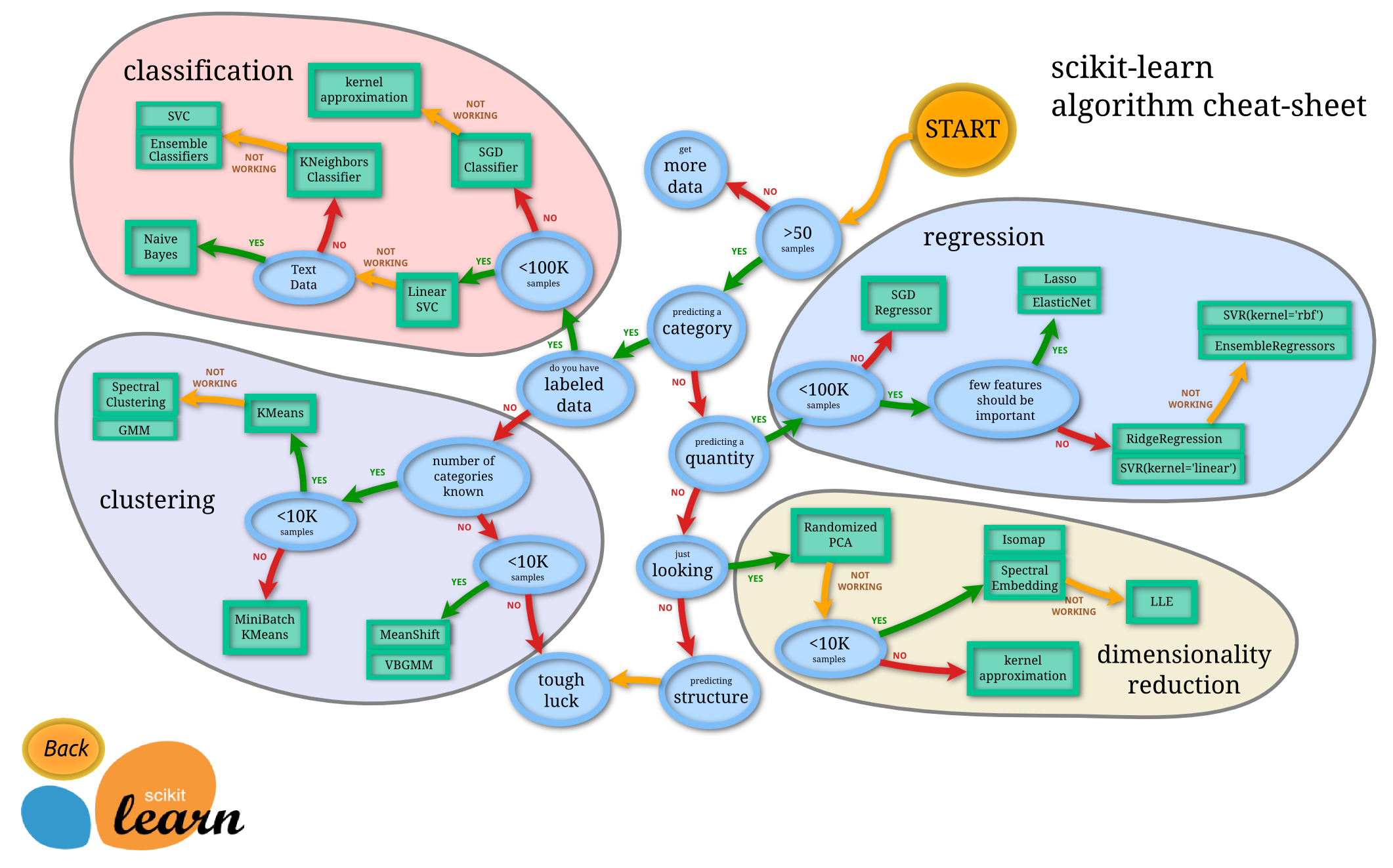
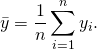如果我們不知道『最小平方法』用來解決什麼問題?
Problem statement
The objective consists of adjusting the parameters of a model function to best fit a data set. A simple data set consists of n points (data pairs) 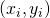 , i = 1, …, n, where
, i = 1, …, n, where 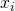 is an independent variable and
is an independent variable and 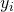 is a dependent variable whose value is found by observation. The model function has the form
is a dependent variable whose value is found by observation. The model function has the form 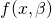 , where m adjustable parameters are held in the vector
, where m adjustable parameters are held in the vector 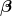 . The goal is to find the parameter values for the model that “best” fits the data. The fit of a model to a data point is measured by its residual, defined as the difference between the actual value of the dependent variable and the value predicted by the model:
. The goal is to find the parameter values for the model that “best” fits the data. The fit of a model to a data point is measured by its residual, defined as the difference between the actual value of the dependent variable and the value predicted by the model:
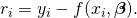
The least-squares method finds the optimal parameter values by minimizing the sum, 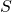 , of squared residuals:
, of squared residuals:
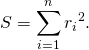
An example of a model in two dimensions is that of the straight line. Denoting the y-intercept as 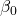 and the slope as
and the slope as 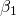 , the model function is given by
, the model function is given by 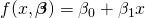 . See linear least squares for a fully worked out example of this model.
. See linear least squares for a fully worked out example of this model.
A data point may consist of more than one independent variable. For example, when fitting a plane to a set of height measurements, the plane is a function of two independent variables, x and z, say. In the most general case there may be one or more independent variables and one or more dependent variables at each data point.
並且對於『線性回歸』的認識止於會意︰
找到適合數據點集之最佳直線!
而不及於其『數學』描述︰
Introduction

In linear regression, the observations red are assumed to be the result of random deviations green from an underlying relationship bluebetween the dependent variable (y) and independent variable (x).
Given a data set  of n statistical units, a linear regression model assumes that the relationship between the dependent variable y and the p-vector of regressors x is linear. This relationship is modeled through a disturbance term or error variable ε — an unobserved random variable that adds “noise” to the linear relationship between the dependent variable and regressors. Thus the model takes the form
of n statistical units, a linear regression model assumes that the relationship between the dependent variable y and the p-vector of regressors x is linear. This relationship is modeled through a disturbance term or error variable ε — an unobserved random variable that adds “noise” to the linear relationship between the dependent variable and regressors. Thus the model takes the form
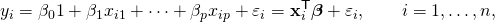
where T denotes the transpose, so that xiTβ is the inner product between vectors xi and β.
Often these n equations are stacked together and written in matrix notation as
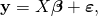
where
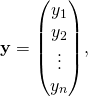
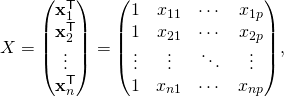
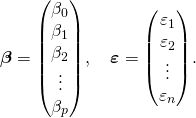
Some remarks on notation and terminology:
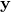 is a vector of observed values
is a vector of observed values 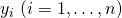 of the variable called the regressand, endogenous variable, response variable, measured variable, criterion variable, or dependent variable. This variable is also sometimes known as the predicted variable, but this should not be confused with predicted values, which are denoted
of the variable called the regressand, endogenous variable, response variable, measured variable, criterion variable, or dependent variable. This variable is also sometimes known as the predicted variable, but this should not be confused with predicted values, which are denoted 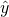 . The decision as to which variable in a data set is modeled as the dependent variable and which are modeled as the independent variables may be based on a presumption that the value of one of the variables is caused by, or directly influenced by the other variables. Alternatively, there may be an operational reason to model one of the variables in terms of the others, in which case there need be no presumption of causality.
. The decision as to which variable in a data set is modeled as the dependent variable and which are modeled as the independent variables may be based on a presumption that the value of one of the variables is caused by, or directly influenced by the other variables. Alternatively, there may be an operational reason to model one of the variables in terms of the others, in which case there need be no presumption of causality.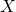 may be seen as a matrix of row-vectors
may be seen as a matrix of row-vectors 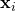 or of n-dimensional column-vectors
or of n-dimensional column-vectors 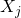 , which are known as regressors, exogenous variables, explanatory variables, covariates, input variables, predictor variables, or independent variables (not to be confused with the concept of independent random variables). The matrix
, which are known as regressors, exogenous variables, explanatory variables, covariates, input variables, predictor variables, or independent variables (not to be confused with the concept of independent random variables). The matrix 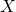 is sometimes called the design matrix.
is sometimes called the design matrix.
- Usually a constant is included as one of the regressors. In particular,
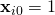 for
for 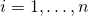 . The corresponding element of β is called the intercept. Many statistical inference procedures for linear models require an intercept to be present, so it is often included even if theoretical considerations suggest that its value should be zero.
. The corresponding element of β is called the intercept. Many statistical inference procedures for linear models require an intercept to be present, so it is often included even if theoretical considerations suggest that its value should be zero.
- Sometimes one of the regressors can be a non-linear function of another regressor or of the data, as in polynomial regression and segmented regression. The model remains linear as long as it is linear in the parameter vector β.
- The values xij may be viewed as either observed values of random variables Xj or as fixed values chosen prior to observing the dependent variable. Both interpretations may be appropriate in different cases, and they generally lead to the same estimation procedures; however different approaches to asymptotic analysis are used in these two situations.
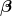 is a
is a 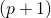 -dimensional parameter vector, where
-dimensional parameter vector, where 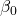 is the intercept term (if one is included in the model—otherwise
is the intercept term (if one is included in the model—otherwise 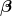 is p-dimensional). Its elements are known as effects or regression coefficients (although the latter term is sometimes reserved for theestimated effects). Statistical estimation and inference in linear regression focuses on β. The elements of this parameter vector are interpreted as the partial derivatives of the dependent variable with respect to the various independent variables.
is p-dimensional). Its elements are known as effects or regression coefficients (although the latter term is sometimes reserved for theestimated effects). Statistical estimation and inference in linear regression focuses on β. The elements of this parameter vector are interpreted as the partial derivatives of the dependent variable with respect to the various independent variables. is a vector of values
is a vector of values 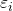 . This part of the model is called the error term, disturbance term, or sometimes noise (in contrast with the “signal” provided by the rest of the model). This variable captures all other factors which influence the dependent variable y other than the regressors x. The relationship between the error term and the regressors, for example their correlation, is a crucial consideration in formulating a linear regression model, as it will determine the appropriate estimation method.
. This part of the model is called the error term, disturbance term, or sometimes noise (in contrast with the “signal” provided by the rest of the model). This variable captures all other factors which influence the dependent variable y other than the regressors x. The relationship between the error term and the regressors, for example their correlation, is a crucial consideration in formulating a linear regression model, as it will determine the appropriate estimation method.
Example. Consider a situation where a small ball is being tossed up in the air and then we measure its heights of ascent hi at various moments in time ti. Physics tells us that, ignoring the drag, the relationship can be modeled as
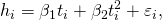
where β1 determines the initial velocity of the ball, β2 is proportional to the standard gravity, and εi is due to measurement errors. Linear regression can be used to estimate the values of β1 and β2 from the measured data. This model is non-linear in the time variable, but it is linear in the parameters β1 and β2; if we take regressors xi = (xi1, xi2) = (ti, ti2), the model takes on the standard form
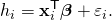
那麼我們能深入理解 scikit-learn 簡單範例之旨趣嗎?


比方問這個『線性模型』好不好呢?
※ 參讀︰

The data sets in the Anscombe’s quartet are designed to have approximately the same linear regression line (as well as nearly identical means, standard deviations, and correlations) but are graphically very different. This illustrates the pitfalls of relying solely on a fitted model to understand the relationship between variables.
A fitted linear regression model can be used to identify the relationship between a single predictor variable xj and the response variable y when all the other predictor variables in the model are “held fixed”. Specifically, the interpretation of βj is the expected change in y for a one-unit change in xj when the other covariates are held fixed—that is, the expected value of the partial derivative of y with respect to xj. This is sometimes called the unique effect of xj on y. In contrast, the marginal effect of xj on y can be assessed using a correlation coefficient or simple linear regression model relating only xj to y; this effect is the total derivative of y with respect to xj.
Care must be taken when interpreting regression results, as some of the regressors may not allow for marginal changes (such as dummy variables, or the intercept term), while others cannot be held fixed (recall the example from the introduction: it would be impossible to “hold ti fixed” and at the same time change the value of ti2).
It is possible that the unique effect can be nearly zero even when the marginal effect is large. This may imply that some other covariate captures all the information in xj, so that once that variable is in the model, there is no contribution of xj to the variation in y. Conversely, the unique effect of xj can be large while its marginal effect is nearly zero. This would happen if the other covariates explained a great deal of the variation of y, but they mainly explain variation in a way that is complementary to what is captured by xj. In this case, including the other variables in the model reduces the part of the variability of y that is unrelated to xj, thereby strengthening the apparent relationship with xj.
The meaning of the expression “held fixed” may depend on how the values of the predictor variables arise. If the experimenter directly sets the values of the predictor variables according to a study design, the comparisons of interest may literally correspond to comparisons among units whose predictor variables have been “held fixed” by the experimenter. Alternatively, the expression “held fixed” can refer to a selection that takes place in the context of data analysis. In this case, we “hold a variable fixed” by restricting our attention to the subsets of the data that happen to have a common value for the given predictor variable. This is the only interpretation of “held fixed” that can be used in an observational study.
The notion of a “unique effect” is appealing when studying a complex system where multiple interrelated components influence the response variable. In some cases, it can literally be interpreted as the causal effect of an intervention that is linked to the value of a predictor variable. However, it has been argued that in many cases multiple regression analysis fails to clarify the relationships between the predictor variables and the response variable when the predictors are correlated with each other and are not assigned following a study design.[9] A commonality analysis may be helpful in disentangling the shared and unique impacts of correlated independent variables.[10]
假使我們也不明白下面『術語』的意義??
In statistics, the mean squared error (MSE) or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors—that is, the average squared difference between the estimated values and what is estimated. MSE is a risk function, corresponding to the expected value of the squared error loss. The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.[1]
The MSE is a measure of the quality of an estimator—it is always non-negative, and values closer to zero are better.
The MSE is the second moment (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the truth). For an unbiased estimator, the MSE is the variance of the estimator. Like the variance, MSE has the same units of measurement as the square of the quantity being estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation (RMSE or RMSD), which has the same units as the quantity being estimated; for an unbiased estimator, the RMSE is the square root of the variance, known as the standard error.
Definition and basic properties
The MSE assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or an estimator (i.e., a mathematical function mapping a sample of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.
Predictor
If a vector of  predictions generated from a sample of n data points on all variables, and
predictions generated from a sample of n data points on all variables, and  is the vector of observed values of the variable being predicted, then the within-sample MSE of the predictor is computed as
is the vector of observed values of the variable being predicted, then the within-sample MSE of the predictor is computed as
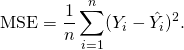
I.e., the MSE is the mean 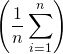 of the squares of the errors
of the squares of the errors 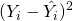 . This is an easily computable quantity for a particular sample (and hence is sample-dependent).
. This is an easily computable quantity for a particular sample (and hence is sample-dependent).
The MSE can also be computed on q data points that were not used in estimating the model, either because they were held back for this purpose or because these data have been newly obtained. In this process, which is known as cross-validation, the MSE is often called the mean squared prediction error, and is computed as
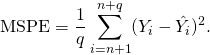
Estimator
The MSE of an estimator 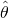 with respect to an unknown parameter
with respect to an unknown parameter 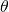 is defined as
is defined as
![Rendered by QuickLaTeX.com \displaystyle \operatorname {MSE} ({\hat {\theta }})=\operatorname {E} _{\theta }\left[({\hat {\theta }}-\theta )^{2}\right].](http://www.freesandal.org/wp-content/ql-cache/quicklatex.com-e152c94378058533be5f868b9ea904e8_l3.png)
This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. Since an MSE is an expectation, it is not a random variable. That being said, the MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data and thus a random variable. If the estimator 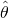 is derived from a sample statistic and is used to estimate some population statistic, then the expectation is with respect to the sampling distribution of the sample statistic.
is derived from a sample statistic and is used to estimate some population statistic, then the expectation is with respect to the sampling distribution of the sample statistic.
The MSE can be written as the sum of the variance of the estimator and the squared bias of the estimator, providing a useful way to calculate the MSE and implying that in the case of unbiased estimators, the MSE and variance are equivalent.[2]
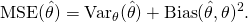
Proof of variance and bias relationship
![Rendered by QuickLaTeX.com \begin{aligned}\operatorname {MSE} ({\hat {\theta }})&=\operatorname {E} _{\theta }\left[({\hat {\theta }}-\theta )^{2}\right]\\&=\operatorname {E} _{\theta }\left[\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]+\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)^{2}\right]\\&=\operatorname {E} _{\theta }\left[\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)^{2}+2\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)+\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)^{2}\right]\\&=\operatorname {E} _{\theta }\left[\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)^{2}\right]+\operatorname {E} _{\theta }\left[2\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)\right]+\operatorname {E} _{\theta }\left[\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)^{2}\right]\\&=\operatorname {E} _{\theta }\left[\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)^{2}\right]+2\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)\operatorname {E} _{\theta }\left[{\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right]+\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)^{2}&&\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta ={\text{const.}}\\&=\operatorname {E} _{\theta }\left[\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)^{2}\right]+2\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)+\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)^{2}&&\operatorname {E} _{\theta }[{\hat {\theta }}]={\text{const.}}\\&=\operatorname {E} _{\theta }\left[\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)^{2}\right]+\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)^{2}\\&=\operatorname {Var} _{\theta }({\hat {\theta }})+\operatorname {Bias} _{\theta }({\hat {\theta }},\theta )^{2}\end{aligned}}](http://www.freesandal.org/wp-content/ql-cache/quicklatex.com-a65e909d058a4c28fff501ce0b8d68b3_l3.png)
……

決定係數 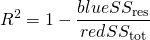 示意圖 線性回歸(右側)的效果比起平均值(左側)越好,決定係數的值就越接近於1。 藍色正方形表示線性回歸的殘差的平方, 紅色正方形數據表示對於平均值的殘差的平方。
示意圖 線性回歸(右側)的效果比起平均值(左側)越好,決定係數的值就越接近於1。 藍色正方形表示線性回歸的殘差的平方, 紅色正方形數據表示對於平均值的殘差的平方。
決定係數(英語:coefficient of determination,記為R2或r2)在統計學中用於度量因變量的變異中可由自變量解釋部分所占的比例,以此來判斷統計模型的解釋力。[1][2][3]
對於簡單線性回歸而言,決定係數為樣本相關係數的平方。[4]當加入其他回歸自變量後,決定係數相應地變為多重相關係數的平方。
假設一數據集包括y1,…,yn共n個觀察值,相對應的模型預測值分別為f1,…,fn。定義殘差ei = yi − fi,平均觀察值為
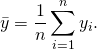
於是可以得到總平方和
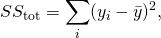
回歸平方和
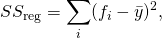
殘差平方和
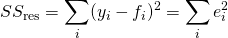
由此,決定係數可定義為
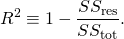
又將要如何回答解釋也!!




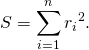

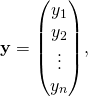
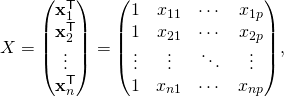
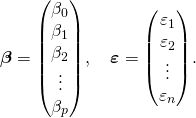



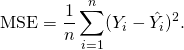
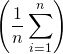 of the squares of the errors
of the squares of the errors 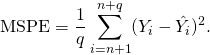
![Rendered by QuickLaTeX.com \begin{aligned}\operatorname {MSE} ({\hat {\theta }})&=\operatorname {E} _{\theta }\left[({\hat {\theta }}-\theta )^{2}\right]\\&=\operatorname {E} _{\theta }\left[\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]+\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)^{2}\right]\\&=\operatorname {E} _{\theta }\left[\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)^{2}+2\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)+\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)^{2}\right]\\&=\operatorname {E} _{\theta }\left[\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)^{2}\right]+\operatorname {E} _{\theta }\left[2\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)\right]+\operatorname {E} _{\theta }\left[\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)^{2}\right]\\&=\operatorname {E} _{\theta }\left[\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)^{2}\right]+2\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)\operatorname {E} _{\theta }\left[{\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right]+\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)^{2}&&\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta ={\text{const.}}\\&=\operatorname {E} _{\theta }\left[\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)^{2}\right]+2\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)+\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)^{2}&&\operatorname {E} _{\theta }[{\hat {\theta }}]={\text{const.}}\\&=\operatorname {E} _{\theta }\left[\left({\hat {\theta }}-\operatorname {E} _{\theta }[{\hat {\theta }}]\right)^{2}\right]+\left(\operatorname {E} _{\theta }[{\hat {\theta }}]-\theta \right)^{2}\\&=\operatorname {Var} _{\theta }({\hat {\theta }})+\operatorname {Bias} _{\theta }({\hat {\theta }},\theta )^{2}\end{aligned}}](http://www.freesandal.org/wp-content/ql-cache/quicklatex.com-a65e909d058a4c28fff501ce0b8d68b3_l3.png)