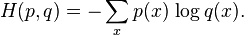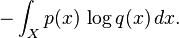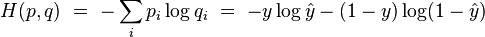《論衡》‧《訂鬼》

凡天地之間有鬼，非人死精神為之也，皆人思念存想之所致也。致之何由？由於疾病。人病則憂懼，憂懼見鬼出。

凡人不病則不畏懼。故得病寢衽，畏懼鬼至。畏懼則存想，存想則目虛見。何以效之？《傳》曰：「伯樂學相馬，顧玩所見，無非馬者。宋之庖丁學解牛，三年不見生牛，所見皆死牛也。」二者用精至矣，思念存想，自見異物也。人病見鬼，猶伯樂之見馬，庖丁之見牛也。伯樂、庖丁所見非馬與牛，則亦知夫病者所見非鬼也。病者困劇身體痛，則謂鬼持箠杖敺擊之，若見鬼把椎鎖繩纆立守其旁，病痛恐懼，妄見之也。初疾畏驚，見鬼之來；疾困恐死，見鬼之怒；身自疾痛，見鬼之擊，皆存想虛致，未必有其實也。夫精念存想，或泄於目，或泄於口，或泄於耳。泄於目，目見其形；泄於耳，耳聞其聲；泄於口，口言其事。晝日則鬼見，暮臥則夢聞。獨臥空室之中，若有所畏懼，則夢見夫人據案其身哭矣。覺見臥聞，俱用精神；畏懼、存想，同一實也。

一曰：人之見鬼，目光與臥亂也。人之晝也，氣倦精盡，夜則欲臥，臥而目光反，反而精神見人物之象矣。人病亦氣倦精盡，目雖不臥，光已亂於臥也，故亦見人物象。病者之見也，若臥若否，與夢相似。當其見也，其人能自知覺與夢，故其見物不能知其鬼與人，精盡氣倦之效也。何以驗之？以狂者見鬼也。狂癡獨語，不與善人相得者，病困精亂也。夫病且死之時，亦與狂等。臥、病及狂，三者皆精衰倦，目光反照，故皆獨見人物之象焉。

一曰：鬼者、人所見得病之氣也。氣不和者中人，中人為鬼，其氣象人形而見。故病篤者氣盛，氣盛則象人而至，至則病者見其象矣。假令得病山林之中，其見鬼則見山林之精。人或病越地者，病見越人坐其側。由此言之，灌夫、竇嬰之徒，或時氣之形象也。凡天地之間，氣皆純於天，天文垂象於上，其氣降而生物。氣和者養生，不和者傷害。本有象於天，則其降下，有形於地矣。故鬼之見也，象氣為之也。眾星之體，為人與鳥獸，故其病人則見人與鳥獸之形。

一曰：鬼者、老物精也。夫物之老者，其精為人；亦有未老，性能變化，象人之形。人之受氣，有與物同精者，則其物與之交。及病，精氣衰劣也，則來犯陵之矣。何以效之？成事：俗間與物交者，見鬼之來也。夫病者所見之鬼，與彼病物何以異？人病見鬼來，象其墓中死人來迎呼之者，宅中之六畜也。及見他鬼，非是所素知者，他家若草野之中物為之也。

一曰：鬼者、本生於人。時不成人，變化而去。天地之性，本有此化，非道術之家所能論辯。與人相觸犯者病，病人命當死，死者不離人。何以明之？《禮》曰：「顓頊氏有三子，生而亡去為疫鬼：一居江水，是為虐鬼；一居若水，是為魍魎鬼；一居人宮室區隅漚庫，善驚人小兒。」前顓頊之世，生子必多，若顓頊之鬼神以百數也。諸鬼神有形體法，能立樹與人相見者，皆生於善人，得善人之氣，故能似類善人之形，能與善人相害。陰陽浮游之類，若雲煙之氣，不能為也。

一曰：鬼者、甲乙之神也。甲乙者、天之別氣也，其形象人。人病且死，甲乙之神至矣。假令甲乙之日病，則死見庚辛之神矣。何則？甲乙鬼，庚辛報甲乙，故病人且死，殺鬼之至者，庚辛之神也。何以效之？以甲乙日病者，其死生之期，常在庚辛之日。此非論者所以為實也。天道難知，鬼神闇昧，故具載列，令世察之也。

一曰：鬼者、物也，與人無異。天地之間，有鬼之物，常在四邊之外，時往來中國，與人雜則，凶惡之類也，故人病且死者乃見之。天地生物也，有人如鳥獸，及其生凶物，亦有似人象鳥獸者。故凶禍之家，或見蜚尸，或見走凶，或見人形，三者皆鬼也。或謂之鬼，或謂之凶，或謂之魅，或謂之魑，皆生存實有，非虛無象類之也。何以明之？成事：俗間家人且凶，見流光集其室，或見其形若鳥之狀，時流人堂室，察其不謂若鳥獸矣。夫物有形則能食，能食則便利。便利有驗，則形體有實矣。《左氏春秋》曰：「投之四裔，以禦魑魅。」《山海經》曰：「北方有鬼國。」說螭者謂之龍物也，而魅與龍相連，魅則龍之類矣。又言「國」、人物之黨也。《山海經》又曰：「滄海之中，有度朔之山，上有大桃木，其屈蟠三千里，其枝間東北曰鬼門，萬鬼所出入也。上有二神人，一曰神荼，一曰鬱壘，主閱領萬鬼。惡害之鬼，執以葦索，而以食虎。於是黃帝乃作禮以時驅之，立大桃人，門戶畫神荼、鬱壘與虎，懸葦索以禦。」凶魅有形，故執以食虎。案可食之物，無空虛者。其物也，性與人殊，時見時匿，與龍不常見，無以異也。

一曰：人且吉凶，妖祥先見。人之且死，見百怪，鬼在百怪之中。故妖怪之動，象人之形，或象人之聲為應，故其妖動不離人形。天地之間，妖怪非一，言有妖，聲有妖，文有妖。或妖氣象人之形，或人含氣為妖。象人之形，諸所見鬼是也；人含氣為妖，巫之類是也。是以實巫之辭，無所因據，其吉凶自從口出，若童之謠矣。童謠口自言，巫辭意自出。口自言，意自出，則其為人，與聲氣自立，音聲自發，同一實也。世稱紂之時，夜郊鬼哭，及倉頡作書，鬼夜哭。氣能象人聲而哭，則亦能象人形而見，則人以為鬼矣。

鬼之見也，人之妖也。天地之間，禍福之至，皆有兆象，有漸不卒然，有象不猥來。天地之道，人將亡，凶亦出；國將亡，妖亦見。猶人且吉，吉祥至；國且昌，昌瑞到矣。故夫瑞應妖祥，其實一也。而世獨謂鬼者不在妖祥之中，謂鬼猶神而能害人，不通妖祥之道，不睹物氣之變也。國將亡，妖見，其亡非妖也。人將死，鬼來，其死非鬼也。亡國者、兵也，殺人者、病也。何以明之？齊襄公將為賊所殺，游于姑棼，遂田于貝丘，見大豕。從者曰：「公子彭生也。」公怒曰：「彭生敢見！」引弓射之，豕人立而啼。公懼，墜于車，傷足，喪履，而為賊殺之。夫殺襄公者，賊也。先見大豕於路，則襄公且死之妖也。人謂之彭生者，有似彭生之狀也。世人皆知殺襄公者非豕，而獨謂鬼能殺人，一惑也。

天地之氣為妖者，太陽之氣也。妖與毒同，氣中傷人者謂之毒，氣變化者謂之妖。世謂童謠，熒惑使之，彼言有所見也。熒惑火星，火有毒熒，故當熒惑守宿，國有禍敗。火氣恍惚，故妖象存亡。龍、陽物也，故時變化。鬼、陽氣也，時藏時見。陽氣赤，故世人盡見鬼，其色純朱。蜚凶、陽也，陽、火也，故蜚凶之類為火光。火熱焦物，故止集樹木，枝葉枯死。《鴻範》五行二曰火，五事二曰言。言、火同氣，故童謠、詩歌為妖言。言出文成，故世有文書之怪。世謂童子為陽，故妖言出於小童。童、巫含陽，故大雩之祭，舞童暴巫。雩祭之禮，倍陰合陽，故猶日食陰勝，攻社之陰也。日食陰勝，故攻陰之類。天旱陽勝，故愁陽之黨。巫為陽黨，故魯僖遭旱，議欲焚巫。巫含陽氣，以故陽地之民多為巫。巫黨於鬼，故巫者為鬼巫。鬼巫比於童謠，故巫之審者，能處吉凶。吉凶能處，吉凶之徒也，故申生之妖見於巫。巫含陽，能見為妖也。申生為妖，則知杜伯、莊子義、厲鬼之徒皆妖也。杜伯之厲為妖，則其弓矢、投、措皆妖毒也。妖象人之形，其毒象人之兵。鬼、毒同色，故杜伯弓矢皆朱彤也。毒象人之兵，則其中人，人輒死也。中人微者即為腓，病者不即時死。何則？腓者、毒氣所加也。

妖或施其毒，不見其體；或見其形，不施其毒；或出其聲，不成其言；或明其言，不知其音。若夫申生，見其體、成其言者也；杜伯之屬，見其體、施其毒者也；詩妖、童謠、石言之屬，明其言者也；濮水琴聲，紂郊鬼哭，出其聲者也。妖之見出也，或且凶而豫見，或凶至而因出。因出，則妖與毒俱行；豫見，妖出不能毒。申生之見，豫見之妖也；杜伯、莊子義、厲鬼至，因出之妖也。周宣王、燕簡公、宋夜姑時當死，故妖見毒因擊。晉惠公身當獲，命未死，故妖直見而毒不射。然則杜伯、莊子義、厲鬼之見，周宣王、燕簡、夜姑且死之妖也。申生之出，晉惠公且見獲之妖也。伯有之夢，駟帶、公孫叚且卒之妖也。老父結草，魏顆且勝之祥，亦或時杜回見獲之妖也。蒼犬噬呂后，呂后且死，妖象犬形也。，武安且卒，妖象竇嬰、灌夫之面也。

故凡世間所謂妖祥、所謂鬼神者，皆太陽之氣為之也。太陽之氣、天氣也。天能生人之體，故能象人之容。夫人所以生者，陰、陽氣也。陰氣主為骨肉，陽氣主為精神。人之生也，陰、陽氣具，故骨肉堅，精氣盛。精氣為知，骨肉為強，故精神言談，形體固守。骨肉精神，合錯相持，故能常見而不滅亡也。太陽之氣，盛而無陰，故徒能為象，不能為形。無骨肉，有精氣，故一見恍惚，輒復滅亡也。

『鬼』不知是何物也？《說文解字》講：鬼，人所歸為鬼。从人，象鬼頭。鬼陰气賊害，从厶。凡鬼之屬皆从鬼。，古文从示。那『鬼』就是『人之歸』耶！東漢王充認為不是『人死精神』為之，『訂』之為『人思念存想之所致』也？！然而

《淮南子》‧《說山訓》有言︰

魄問於魂曰：「道何以為體？」曰：「以無有為體。」魄曰：「無有有形乎？」魂曰：「無有。」「何得而聞也？」魂曰：「吾直有所遇之耳。視之無形，聽之無聲，謂之幽冥。幽冥者，所以喻道，而非道也。魄曰：「吾聞得之矣。乃內視而自反也。」魂曰：「凡得道者，形不可得而見，名不可得而揚。今汝已有形名矣，何道之所能乎！」魄曰：「言者，獨何為者？」「吾將反吾宗矣。」魄反顧，魂忽然不見，反而自存，亦以淪於無形矣。

人不小學，不大迷；不小慧，不大愚。人莫鑒於沫雨，而鑒於澄水者，以其休止不蕩也。詹公之釣，千歲之鯉不能避；曾子攀柩車，引楯者為之止也；老母行歌而動申喜，精之至也；瓠巴鼓瑟，而淫魚出聽；伯牙鼓琴，駟馬仰秣；介子歌龍蛇，而文君垂泣。故玉在山而草木潤，淵生珠而岸不枯。螾無筋骨之強，爪牙之利，上食晞堁，下飲黃泉，用心一也。清之為明，杯水見眸子；濁之為暗，河水不見太山。視日者眩，聽雷者聾；人無為則治，有為則傷。無為而治者，載無也；為者，不能有也；不能無為者，不能有為也。人無言而神，有言則傷。無言而神者載無，有言則傷其神。之神者，鼻之所以息，耳之所以聽，終以其無用者為用矣。

……

畏馬之辟也，不敢騎；懼車之覆也，不敢乘；是以虛禍距公利也。不孝弟者，或詈父母。生子者，所不能任其必孝也，然猶養而長之。範氏之敗，有竊其鍾負而走者，鎗然有聲，懼人聞之，遽掩其耳。憎人聞之，可也；自掩其耳，悖矣。升之不能大於石也，升在石之中；夜不能修其歲也，夜在歲之中；仁義之不能大於道德也，仁義在道德之包。先針而後縷，可以成帷；先縷而後針，不可以成衣。針成幕，蔂成城。事之成敗，必由小生。言有漸也。染者先青而後黑則可，先黑而後青則不可；工人下漆而上丹則可，下丹而上漆則不可。萬事由此，所先後上下，不可不審。水濁而魚噞，形勞而神亂。故國有賢君，折沖萬里。因媒而嫁，而不因媒而成；因人而交，不因人而親。行合趨同，千里相從；行不合，趨不同，對門不通。海水雖大，不受胔芥，日月不應非其氣，君子不容非其類也。人不愛倕之手，而愛己之指，不愛江、漢之珠，而愛己之鉤。以束薪為鬼，以火煙為氣。以束薪為鬼，朅而走；以火煙為氣，殺豚烹狗。先事如此，不如其後。巧者善度，知者善豫。羿死桃部，不給射；慶忌死劍鋒，不給搏。滅非者戶告之曰：「我實不與我諛亂。」謗乃愈起。止言以言，止事以事，譬猶揚堁而弭塵，抱薪而救火。流言雪汙，譬猶以涅拭素也。

───

，或以為『鬼』乃『束薪火煙』耶！！？？

『抽象事物』既已『抽象』，故『無象』可見，不過尚有『定義』在焉︰

$\bigcirc \ln \square + (1- \bigcirc ) \ln (1- \square)$

，因而無需玄想、不必狐疑，自可原理推論矣。所以莫問

Cross entropy

In information theory, the cross entropy between two probability distributions $p$ and $q$ over the same underlying set of events measures the average number of bits needed to identify an event drawn from the set, if a coding scheme is used that is optimized for an “unnatural” probability distribution $q$ , rather than the “true” distribution $p$ .

The cross entropy for the distributions $p$ and $q$ over a given set is defined as follows:

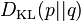H(p, q) = \operatorname{E}_p[-\log q] = H(p) + D_{\mathrm{KL}}(p \| q),\!

where $H(p)$ is the entropy of $p$ , and $D_{\mathrm{KL}}(p || q)$ is the Kullback–Leibler divergence of $q$ from $p$ (also known as the relative entropy of p with respect to q — note the reversal of emphasis).

For discrete $p$ and $q$ this means

H(p, q) = -\sum_x p(x)\, \log q(x). \!

The situation for continuous distributions is analogous:

-\int_X p(x)\, \log q(x)\, dx. \!

NB: The notation $H(p,q)$ is also used for a different concept, the joint entropy of $p$ and $q$ .

……

Cross-entropy error function and logistic regression

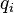Cross entropy can be used to define the loss function in machine learning and optimization. The true probability $p_i$ is the true label, and the given distribution $q_i$ is the predicted value of the current model.

More specifically, let us consider logistic regression, which (in its most basic form) deals with classifying a given set of data points into two possible classes generically labelled $0$ and $1$ . The logistic regression model thus predicts an output $y\in\{0,1\}$ , given an input vector $\mathbf{x}$ . The probability is modeled using the logistic function $g(z)=1/(1+e^{-z})$ . Namely, the probability of finding the output $y=1$ is given by

q_{y=1}\ =\ \hat{y}\ \equiv\ g(\mathbf{w}\cdot\mathbf{x})\,,

where the vector of weights 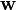$\mathbf{w}$ is learned through some appropriate algorithm such as gradient descent. Similarly, the conjugate probability of finding the output 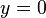$y=0$ is simply given by

q_{y=0}\ =\ 1-\hat{y}

The true (observed) probabilities can be expressed similarly as $p_{y=1}=y$ and $p_{y=0}=1-y$ .
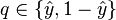Having set up our notation, $p\in\{y,1-y\}$ and $q\in\{\hat{y},1-\hat{y}\}$ , we can use cross entropy to get a measure for similarity between $p$ and $q$ :

H(p,q)\ =\ -\sum_ip_i\log q_i\ =\ -y\log\hat{y} - (1-y)\log(1-\hat{y})

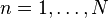The typical loss function that one uses in logistic regression is computed by taking the average of all cross-entropies in the sample. For example, suppose we have $N$ samples with each sample labeled by $n=1,\dots,N$ . The loss function is then given by:

\text{[math]}

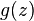where $\hat{y}_n\equiv g(\mathbf{w}\cdot\mathbf{x}_n)$ , with $g(z)$ the logistic function as before.
The logistic loss is sometimes called cross-entropy loss. It’s also known as log loss (In this case, the binary label is often denoted by {-1,+1}).^[1]

───

是什麼？直須了解『此物定義』即可！事實上『它的意義』人們還在探索中，『熱力學』與『統計力學』也不曾見其跡蹤`。如是可知 Michael Nielsen 先生行文之為難也︰

Introducing the cross-entropy cost function

How can we address the learning slowdown? It turns out that we can solve the problem by replacing the quadratic cost with a different cost function, known as the cross-entropy. To understand the cross-entropy, let’s move a little away from our super-simple toy model. We’ll suppose instead that we’re trying to train a neuron with several input variables, $x_1, x_2, \ldots$ $x_{1}, x_{2}, \dots$ , corresponding weights $w_1, w_2, \ldots$ $w_{1}, w_{2}, \dots$ , and a bias, $b$ $b$ :

The output from the neuron is, of course, $a = \sigma(z)$

a = σ (z)

, where $z = \sum_j w_j x_j+b$

z = \sum_{j} w_{j} x_{j} + b

is the weighted sum of the inputs. We define the cross-entropy cost function for this neuron by

C = -\frac{1}{n} \sum_x \left[y \ln a + (1-y ) \ln (1-a) \right], \ \ \ \ (57)

where $n$ $n$ is the total number of items of training data, the sum is over all training inputs, $x$ $x$ , and $y$ $y$ is the corresponding desired output.

It’s not obvious that the expression (57) fixes the learning slowdown problem. In fact, frankly, it’s not even obvious that it makes sense to call this a cost function! Before addressing the learning slowdown, let’s see in what sense the cross-entropy can be interpreted as a cost function.

Two properties in particular make it reasonable to interpret the cross-entropy as a cost function. First, it’s non-negative, that is, $C > 0$ $C > 0$ . To see this, notice that: (a) all the individual terms in the sum in (57) are negative, since both logarithms are of numbers in the range $0$ $0$ to $1$ $1$ ; and (b) there is a minus sign out the front of the sum.

Second, if the neuron’s actual output is close to the desired output for all training inputs, $x$ $x$ , then the cross-entropy will be close to zero*

*To prove this I will need to assume that the desired outputs $y$ are all either $0$ $0$ or $1$ $1$ . This is usually the case when solving classification problems, for example, or when computing Boolean functions. To understand what happens when we don’t make this assumption, see the exercises at the end of this section.

. To see this, suppose for example that $y = 0$ $y = 0$ and $a \approx 0$ $a \approx 0$ for some input $x$ $x$ . This is a case when the neuron is doing a good job on that input. We see that the first term in the expression (57) for the cost vanishes, since $y = 0$ $y = 0$ , while the second term is just $-\ln (1-a) \approx 0$ $- \ln (1 - a) \approx 0$ . A similar analysis holds when $y = 1$ $y = 1$ and $a \approx 1$ $a \approx 1$ . And so the contribution to the cost will be low provided the actual output is close to the desired output.

Summing up, the cross-entropy is positive, and tends toward zero as the neuron gets better at computing the desired output, $y$ $y$ , for all training inputs, $x$ $x$ . These are both properties we’d intuitively expect for a cost function. Indeed, both properties are also satisfied by the quadratic cost. So that’s good news for the cross-entropy. But the cross-entropy cost function has the benefit that, unlike the quadratic cost, it avoids the problem of learning slowing down. To see this, let’s compute the partial derivative of the cross-entropy cost with respect to the weights. We substitute $a = \sigma(z)$ $a = σ (z)$ into (57), and apply the chain rule twice, obtaining:

\frac{\partial C}{\partial w_j} & = & -\frac{1}{n} \sum_x \left( \frac{y }{\sigma(z)} -\frac{(1-y)}{1-\sigma(z)} \right) \frac{\partial \sigma}{\partial w_j} \ \ \ \ (58)

= -\frac{1}{n} \sum_x \left( \frac{y}{\sigma(z)} -\frac{(1-y)}{1-\sigma(z)} \right)\sigma'(z) x_j. \ \ \ \ (59)

Putting everything over a common denominator and simplifying this becomes:

\frac{\partial C}{\partial w_j} & = & \frac{1}{n} \sum_x \frac{\sigma'(z) x_j}{\sigma(z) (1-\sigma(z))} (\sigma(z)-y). \ \ \ \ (60)

Using the definition of the sigmoid function, $\sigma(z) = 1/(1+e^{-z})$ $σ (z) = 1 / (1 + e^{- z})$ , and a little algebra we can show that $\sigma'(z) = \sigma(z)(1-\sigma(z))$ $σ^{'} (z) = σ (z) (1 - σ (z))$ . I’ll ask you to verify this in an exercise below, but for now let’s accept it as given. We see that the $\sigma'(z)$ $σ^{'} (z)$ and $\sigma(z)(1-\sigma(z))$ $σ (z) (1 - σ (z))$ terms cancel in the equation just above, and it simplifies to become:

\frac{\partial C}{\partial w_j} = \frac{1}{n} \sum_x x_j(\sigma(z)-y). \ \ \ \ (61)

This is a beautiful expression. It tells us that the rate at which the weight learns is controlled by $\sigma(z)-y$ $σ (z) - y$ , i.e., by the error in the output. The larger the error, the faster the neuron will learn. This is just what we’d intuitively expect. In particular, it avoids the learning slowdown caused by the $\sigma'(z)$ $σ^{'} (z)$ term in the analogous equation for the quadratic cost, Equation (55). When we use the cross-entropy, the $σ^{'} (z)$ term gets canceled out, and we no longer need worry about it being small. This cancellation is the special miracle ensured by the cross-entropy cost function. Actually, it’s not really a miracle. As we’ll see later, the cross-entropy was specially chosen to have just this property.

In a similar way, we can compute the partial derivative for the bias. I won’t go through all the details again, but you can easily verify that

\frac{\partial C}{\partial b} = \frac{1}{n} \sum_x (\sigma(z)-y). \ \ \ \ (62)

Again, this avoids the learning slowdown caused by the $\sigma'(z)$ $σ^{'} (z)$ term in the analogous equation for the quadratic cost, Equation (56).

───

彷彿『cross-entropy』只是為著解決『the learning slowdown 』而生乎！！？？

日	一	二	三	四	五	六
« 4 月				6 月 »
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30	31

FreeSandal

每日彙整: 2016-05-23

W!o+ 的《小伶鼬工坊演義》︰神經網絡【學而堯曰】三

Cross entropy

Cross-entropy error function and logistic regression

Introducing the cross-entropy cost function

輕。鬆。學。部落客