一九九零年發射的『哈伯太空望遠鏡』 HST Hubble Space Telescope 是以美國著名的天文學家『愛德溫‧鮑威爾‧哈伯』 Edwin Powell Hubble 為名，是一架在地球軌道上的望遠鏡。由於它位於地球大氣層之上，因此獲得了地上望遠鏡所沒有的好處：影像不受大氣湍流的影響、視相度極好，更無大氣散射造成的背景光干擾，甚至能觀測會被臭氧層吸收的紫外線。『哈伯太空望遠鏡』彌補了地面觀測的不足，幫助天文學家『理解』和『解答』了許多天文學上的『基本問題』，使得人類對『宇宙緣起』有了更深的『認識』。

『約翰‧卡爾‧弗里德里希‧高斯』 Johann Karl Friedrich Gauß 【Gauss】是德國著名數學家、物理學家、天文學家和大地測量學家，生於布倫瑞克，卒於哥廷根。高斯被認為是歷史上最重要的數學家之一，而且有『數學王子』的美譽。一八零八年，在高斯的數學巨著《算術研究》 Disquisitiones Arithmeticae 首度出現了一個形式符號 它表示等於或小於實數 的『最大整數』，也就是說 。今天這個『高斯符號』又稱之為『底函數』  floor function ，與另一『頂函數』 ── 是指比實數 大的『最小整數』 ── ceiling functions 成為一對，經常出現於『數學』和『計算機科學』之中。這個『高斯符號』有什麼重要的嗎？通常一個好的『符號』能使人清晰『表達』複雜和困難的『概念』，而且讓人容易『理解』所說的『內容』，因此是十分重要的啊！！

舉例來說，歐拉研究過『調和級數』 harmonic series  和『自然對數』 natural logarithm  之間的關係，雖然這兩者都是『發散的』 ──  值為無限大 ── 它們的『差值』卻是一個叫做『歐拉-馬歇羅尼常數』的 值。它可以定義如下

.
，計算後得到

。 對一個不是『整數』的實數 ，『高斯函數』也可以表示為

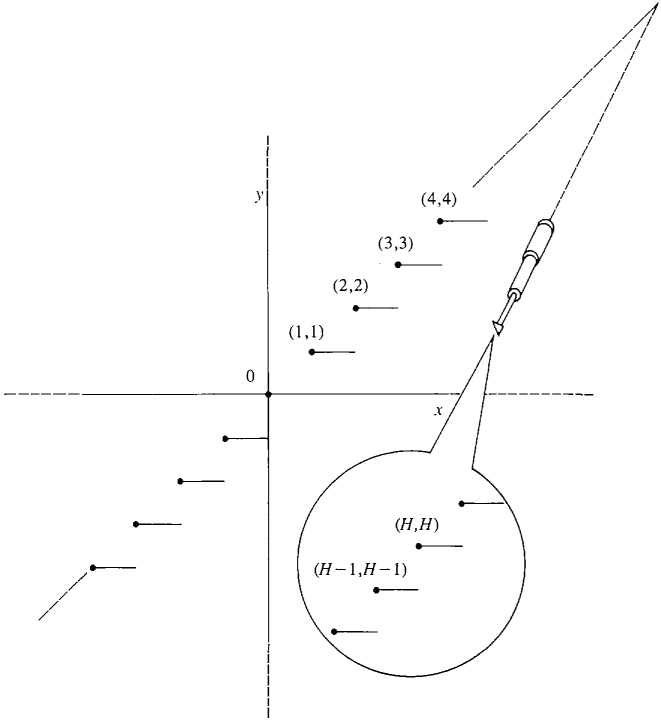
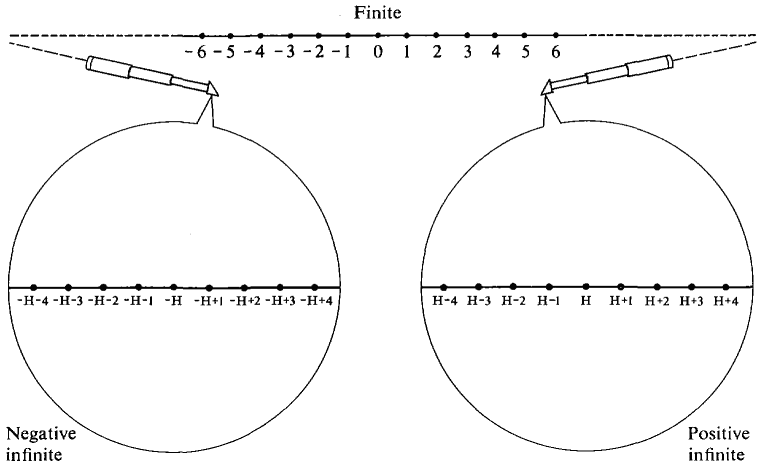
。因此說『超實數系』裡也有『超整數』 hyperinteger 這就一點也不奇怪了吧！如果只從『形式定義』上講，一個『超整數』就是一個『超實數』的『整數部份』，也就是說

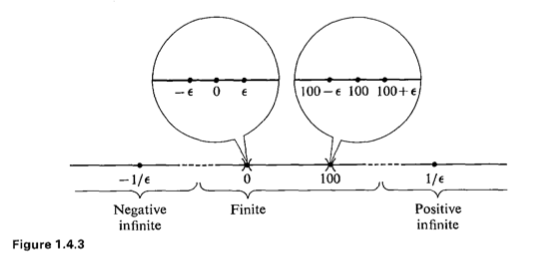
， 可能沒有什麼意思。假使設想『超實數系』既有『無窮小』 ，那它的『倒數』 reciprocal 就是『無限大』，也可以叫做『巨量』 Huge，一般用 表示。如果說『某數』 是個『巨量』，就是講 是『無窮小』數 ，這樣 、、 和 又是些什麼樣的數呢？它們被稱作『未定式』 Indeterminate form，因為假使不知道它們的『來歷』，我們並不能『確定』最終的『運算結果』 ── 是無窮小、有限量或是無限大 ── 。純就『形式』上講，它門是 、、 與 的計算，然而這可在『代數運算』是不被允許的啊！但是如果，那麼不管說 多大多小 ，因此即使 是『正無窮小』數 ，也應該得到 的『極限結果』的吧！同樣的 是『趨近』於『無限大』的啊！也就是說『無窮小』與『無限大』也是有『等級』 Order 的，如果忽略了『這件事』，隨便混談『至大』和『至小』，大概就是『非量』與『非非量』的『迷惑』之所從來的了！！

舉例來說，左圖中『三角形』 的面積，小於『扇形』 ，更小於『四邊形』 ，於是

，因此

，然而 ，所以說 的啊！也可以講當 很小的時候， 和 是『同等級』的啊！！

假使我們想像『巨量 – 巨量 = 常量』的『情況』，就彷彿是用著超級『望遠鏡』來『觀察』遙遠的『銀河系』，然而因為『太遙遠』了，有時它不過祇是天上的『一點』亮光，甚至它的『附近』還有著『星光』點點，這難到說就是『超整數』所想『描繪』的『天文圖象』的嗎？？

由於『無窮小』數滿足『代數法則』，自然人們自可將『狄拉克 函數』看成『底為 高為 的矩形』，從『直覺』上掌握物理上『衝量』 impulse 一詞所指的『情境』的啊！！