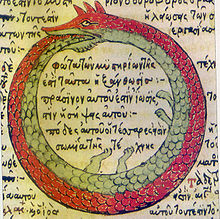
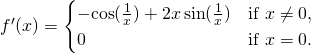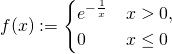『銜尾蛇』 Ouroboros οὐροβόρος 也被叫做『咬尾蛇』,是一個自古流傳至今的『符號』,形象為一條蛇正在吞食著自己的尾巴,結果呈現出一個『圓環』形狀,有時也表現成數字『8』的樣子,意指『自我吞食者』。這個符號一直都有著多種的『象徵』意義,一般以『無限大』與『循環』最為人們所熟知。此外,『銜尾蛇』也是宗教及神話裡的常見符號,在煉金術中更是重要的『徽記』。知名的心理學家『榮格』認為『銜尾蛇』其實是反映了人類的『心理原型』。
古羅馬時期,埃及的一個『諾斯替教的寶石』 Gnostic gem ,上面刻有『魔法文字』magic words,一隻『銜尾蛇』環繞在『魔法文字』與『聖甲蟲』scarab 之外。作者不知它在述說些什麼的呢?
有人講『銜尾蛇』和『西藏石刻』裡有名的『無盡之結』圖案一樣,都是代表著『生死循環』的概念,也可能是數學上『無限大』的符號『∞』的最初來源。
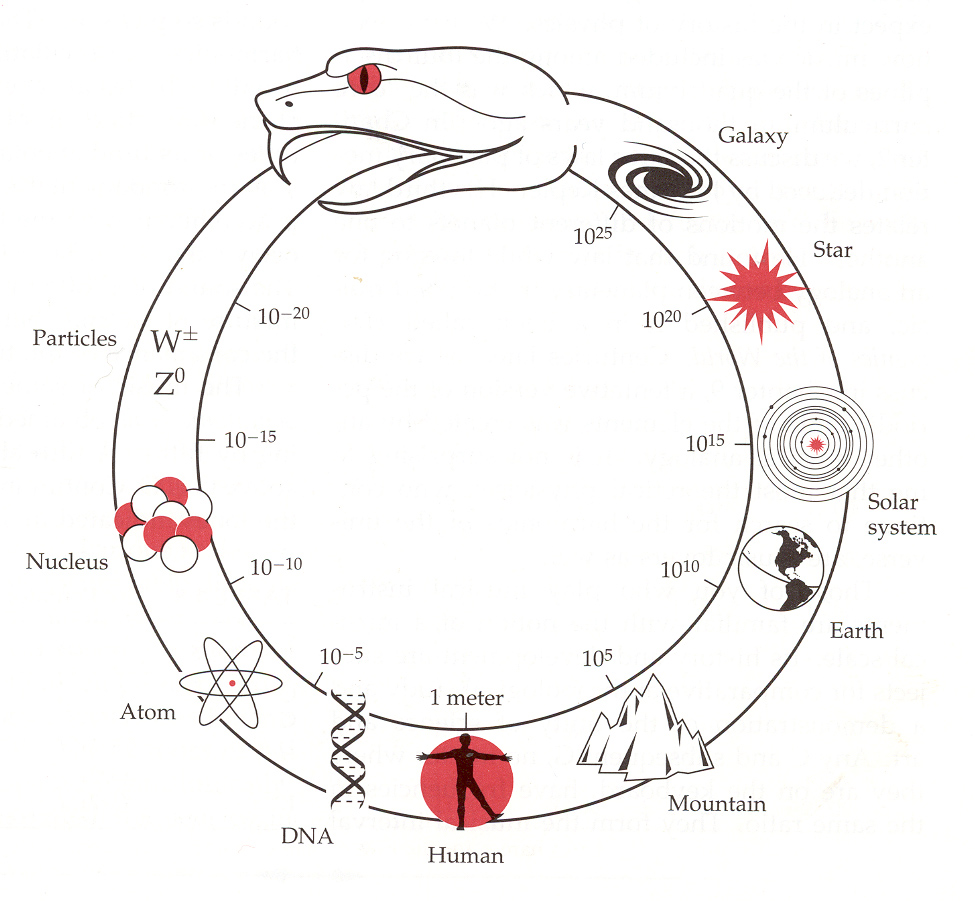
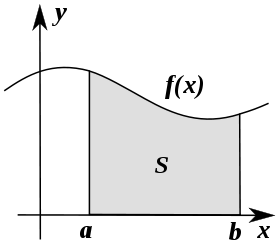
美國羅徹斯特大學 University of Rochester 的天文與物理教授 Douglas Cline 用『這個圖案』表示『物理統一性』the unity of physics 的『象徵』。除了象徵『無窮』以外,還『印證』了宇宙中『無始無終』的循環概念,是『極小的粒子』與『極大之宇宙』概念的交接。
根據現今物理學的觀念,物質可以分解成分子、原子與基本粒子等等構成單元,然而越是了解『微觀世界』的現象,卻反而越能解釋『巨觀宇宙』的運作規律。一九九三年荷蘭物理學家 Gerard ‘t Hooft 提出︰在一個以『普朗克長度』 ![]() 為邊長的面積,大約只能夠存放『一位元』的資訊,在接近普朗克的尺度下,古典的『重力理論』必須要把『量子效應』考慮進去。今天尚未獲得證明的『全像原理』告訴我們:和任何表面相鄰的區域,可以擁有的資訊量都有一個最大值。 也就是說,一個屋子可以容納的『資訊量』,並不是由這個屋子的『體積』來決定的,反而受限於這個屋子外牆的『面積』。
為邊長的面積,大約只能夠存放『一位元』的資訊,在接近普朗克的尺度下,古典的『重力理論』必須要把『量子效應』考慮進去。今天尚未獲得證明的『全像原理』告訴我們:和任何表面相鄰的區域,可以擁有的資訊量都有一個最大值。 也就是說,一個屋子可以容納的『資訊量』,並不是由這個屋子的『體積』來決定的,反而受限於這個屋子外牆的『面積』。
這樣說來大天使『加百利之號角』擁有『無限大』的『資訊量』的吧!!
在『微積分』的發展史中,『費馬』聲稱他借用了『丟番圖』的成就,引入了『足量』概念,這等同於說『誤差』是『無窮小』。然而他未能體會兩者之間的密切關係。之後英國數學家『約翰‧沃利斯』 John Wallis 、『伊薩克‧巴羅』 Isaac Barrow 和『詹姆士‧格里高利』 Gregory of Tours 都有很大的貢獻。雖然『牛頓』的老師巴羅雖然知道『微分』與『積分』這兩者之間有『互逆』的關係,由於求『導數』還沒有一套有系統的計算方法,也許他不能認知此種關係的意義。更因為古希臘平面幾何的成功給予西方數學非常深遠的影響,一般多認為只有『幾何論證』之方法才是『嚴謹的』和『真正的』數學,所謂的『代數』不過是個輔助的工具罷了。在笛卡兒以及費馬大力倡導以『代數』的方法研究『幾何問題』,這種態度才漸漸有了轉變。可是那時『代數方法』仍然未臻於成熟,而且『實數系統』遲遲未能夠建立,因此許多數學家仍然固守『幾何陣營』。牛頓雖然放棄了他老師的『純幾何』觀點,並且發展出了有效的『微分』方法,不過他始終未敢直接發表。牛頓他雖然利用了『微積分』的技巧,並由『萬有引力』以及『三大運動定律』作出發說明了他的『宇宙體系』,解決了『天體運動』、『流體旋轉』之 曲面、『地球扁率』,與『擺線』上重物的運動等等問題。但是『牛頓』在一六八七年的巨著《自然哲學的數學原理》中仍把『微積分』的跡痕抹去,僅以古典的『幾何論證』方式作論述。或許他擔心時人的批評,明知道『這些方法』 ── 乘積法則、鏈式法則、高階導數、泰勒級數和解析方程式…… ── 卻因為『無窮小』在當時仍然飽受非議,故而保持沉默一言不語。
其後德國哲學家與數學家『哥特佛萊德‧威廉‧萊布尼茲』 Gottfried Wilhelm Leibniz ── 一位歷史上少見的通才,被譽為十七世紀的『亞里士多德』 ── 創造了基於『無窮小』觀念的『微積分』學,雖然那時曾被『牛頓』指責為『抄襲』,然而『萊布尼茨』到今天都被認為是『獨立』發明微積分的另一人。他的『風格嚴密』又『注重形式』且研究『適切符號』,帶來了現今在『微積分』裡『表達式』常用的『記號法』。
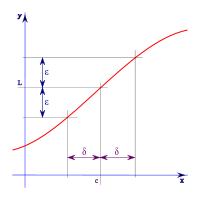
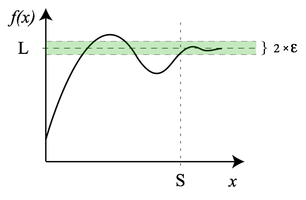
由於『無窮小』量必為『非量』的『爭議不斷』,一八二零年時法國數學家奧古斯丁‧路易‧柯西 Augustin Louis Cauchy 提出了『(ε, δ)極限定義』,之後德國數學家卡爾‧特奧多爾‧威廉‧魏爾斯特拉斯 Karl Theodor Wilhelm Weierstraß ── 現代分析之父 ── 總結了『極限』 limit 的概念,終於迴避了『無窮小』的觀念。自此『微積分』就以『極限』作為基礎,而『無窮小』就成歷史雲煙的了!
何謂『連續』 continuity 函數的呢?『魏爾斯特拉斯』這麼說︰
『函數』![]() 在
在 ![]() 是『連續的』,是講假使對『任意』的
是『連續的』,是講假使對『任意』的 ![]() ,都『存在』一個
,都『存在』一個 ![]() 它能夠使所有在
它能夠使所有在 ![]() 『論域』中的
『論域』中的 ![]() 都得到
都得到 ![]() 的話,如此我們就說
的話,如此我們就說 ![]() 在
在 ![]() 是『連續的』!!
是『連續的』!!
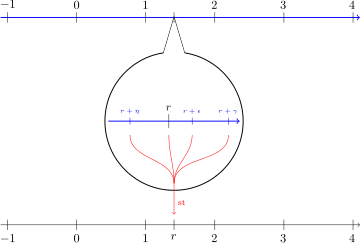
在《吃一節 TCPIP!!中》一文中我們談到了『拓撲學』 Topology 一詞源自希臘文『地點之研究』,始於歐拉柯尼斯堡的七橋問題。這門數學探討『連通性』 connectedness 、『連續性』 continuity 、以及『邊界』 boundary。它不用東西的『形狀』來作分類,而是分析在那個東西裡所有連通的點,各個連續的區域,和有哪些分別內外的邊界。假使從『拓撲學』的觀點來談『函數』的『連續性』,那麼 ![]() 就是
就是 ![]() 的『鄰域』 neighborhood,而
的『鄰域』 neighborhood,而 ![]() 也就是
也就是 ![]() 的『鄰域』 。所以函數上『一點』的連續性是說『這個點』的所有『指定鄰域』,都有一個『實數區間』── 鄰域的另一種說法 ── 與之『對應』,『此函數』將『此區間』映射到那個『指定鄰域』裡。
的『鄰域』 。所以函數上『一點』的連續性是說『這個點』的所有『指定鄰域』,都有一個『實數區間』── 鄰域的另一種說法 ── 與之『對應』,『此函數』將『此區間』映射到那個『指定鄰域』裡。
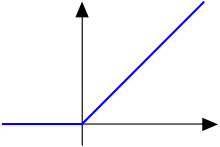
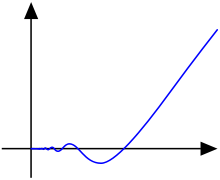
然而一個函數在『某個點』的『連續性』,並不能夠『確保』在『那個點』的『斜率存在』 ── 或說『可微分性』,比方說
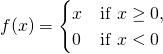
,當 ![]() 時,『斜率』是
時,『斜率』是 ![]() ,在
,在 ![]() 時,『斜率』為
時,『斜率』為 ![]() ,然而
,然而 ![]() 時『斜率』不存在!這使得我們必須研究一個函數在『每個點』之『鄰域』情況,於是數學步入了『解析的』 Analytic 時代。所謂『解析的』一詞是指『這類函數』在
時『斜率』不存在!這使得我們必須研究一個函數在『每個點』之『鄰域』情況,於是數學步入了『解析的』 Analytic 時代。所謂『解析的』一詞是指『這類函數』在 ![]() 的『鄰域』,可以用『泰勒級數』來作展開
的『鄰域』,可以用『泰勒級數』來作展開
![]()
。於是一個『解析函數』在定義域的『每一點』上都是『無窮階可導』的。人們將『無窮階可導』的函數,又稱之為『光滑函數』 smooth function。然而『可導性』卻不同於『連續性』,因此又定義了『連續可導性』︰假使一個函數從『一階到 N 階』的導數都『存在』而且『連續』,我們稱之為 ![]() 類函數。舉例來說
類函數。舉例來說
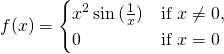
雖然『一階導數』存在但是在 ![]() 時,並不『連續』,所以它只能屬於
時,並不『連續』,所以它只能屬於 ![]() 類,而不是屬於
類,而不是屬於 ![]() 類。
類。
雖然一個『光滑函數』就屬於 ![]() 類,但是它可以不是『解析函數』,比方說
類,但是它可以不是『解析函數』,比方說
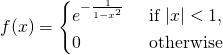
是『光滑的』,然而在 ![]() 時無法用『泰勒級數』來作展開,因此不是『解析的』。
時無法用『泰勒級數』來作展開,因此不是『解析的』。
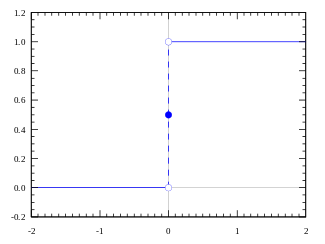
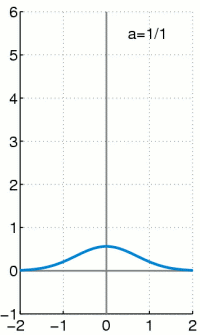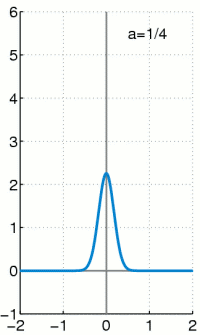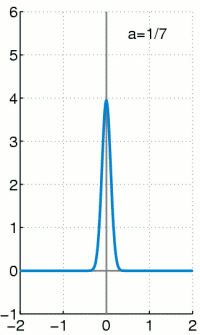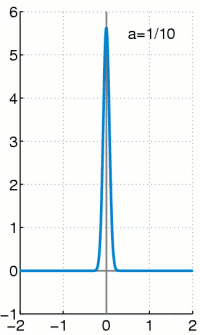
縱使人們覺得『連續』與『鄰近』以及『導數』和『光滑』彼此之間有聯繫,由於失去『直觀』的導引,『概念』卻又越來越『複雜』,因此『微積分』也就遠離了一般人的『理解』,彷彿鎖在『解析』與『極限』的『巴別塔』中!更不要說還有一些『很有用』卻是『很奇怪』的函數。舉例來說,『單位階躍』函數,又稱作『黑維塞階躍函數』 Heaviside step function ,可以定義如下
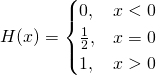
,在 ![]() 時是『不連續』的,它可以『解析』為
時是『不連續』的,它可以『解析』為
![]()
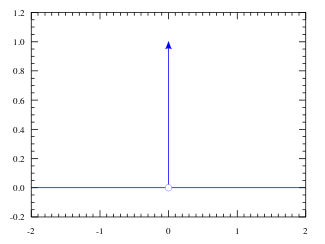
,它的『微分』是 ![]() ,而且這個『狄拉克
,而且這個『狄拉克 ![]() 函數』 Dirac Delta function 是這樣定義的
函數』 Dirac Delta function 是這樣定義的
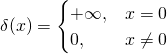
,滿足
![]()
。怕是想『解析』一下都令人頭大,『極限』和『微分』與『積分』能不能『交換次序』,它必須滿足『什麼條件』,假使再加上『無限級數』求和,
![]()
,果真是我的天啊的吧!!
一九六零年,德國數學家『亞伯拉罕‧魯濱遜』 Abraham Robinson 將『萊布尼茲』的微分直觀落實。 用嚴謹的方法來定義和運算實數的『無窮小』與『無限大』,這就是數學史上著名的『非標準微積分』Non-standard calculus ,可說是『非標準分析』non-standard analysis 之父。
就像『複數』 ![]() 是『實數系』
是『實數系』 ![]() 的『擴張』一樣,他將『實數系』增入了『無窮小』 infinitesimals 元素
的『擴張』一樣,他將『實數系』增入了『無窮小』 infinitesimals 元素 ![]() ,魯濱遜創造出『超實數』 hyperreals
,魯濱遜創造出『超實數』 hyperreals ![]() ,形成了『超實數系』
,形成了『超實數系』 ![]() 。那這個『無窮小』是什麼樣的『數』呢?對於『正無窮小』來說,任何給定的『正數』都比要它大,就『負無窮小』來講,它大於任何給定的『負數』。 『零』也就自然的被看成『實數系』裡的『無窮小』的了。假使我們說兩個超實數
。那這個『無窮小』是什麼樣的『數』呢?對於『正無窮小』來說,任何給定的『正數』都比要它大,就『負無窮小』來講,它大於任何給定的『負數』。 『零』也就自然的被看成『實數系』裡的『無窮小』的了。假使我們說兩個超實數 ![]() 是『無限的鄰近』 indefinitly close,記作
是『無限的鄰近』 indefinitly close,記作 ![]() 是指
是指 ![]() 是個『無窮小』量。在這個觀點下,『無窮小』量不滿足『實數』的『阿基米德性質』。也就是說,對於任意給定的
是個『無窮小』量。在這個觀點下,『無窮小』量不滿足『實數』的『阿基米德性質』。也就是說,對於任意給定的 ![]() 來講,
來講, ![]() 為『無窮小』量;而
為『無窮小』量;而 ![]() 是『無限大』量。然而在『系統』與『自然』的『擴張』下,『超實數』的『算術』符合所有一般『代數法則』。
是『無限大』量。然而在『系統』與『自然』的『擴張』下,『超實數』的『算術』符合所有一般『代數法則』。
有人把『超實數』想像成『數原子』,一個環繞著『無窮小』數的『實數』。就像『複數』有『實部』 ![]() 與『虛部』
與『虛部』 ![]() 取值『運算』一樣,『超實數』也有一個取值『運算』叫做『標準部份函數』Standard part function
取值『運算』一樣,『超實數』也有一個取值『運算』叫做『標準部份函數』Standard part function
![]()
![]()
。 如此一個『函數』 ![]() 在
在 ![]() 是『連續的』就可以表示成『如果
是『連續的』就可以表示成『如果 ![]() ,可以得到
,可以得到 ![]() 』。
』。
假使 ![]() ,那麼
,那麼 ![]() 的『斜率』就可以這麼計算
的『斜率』就可以這麼計算
![]()
![]()
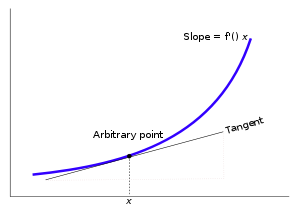
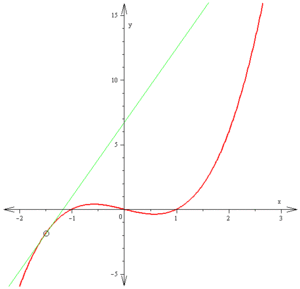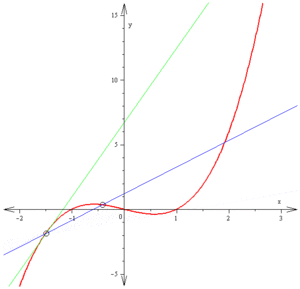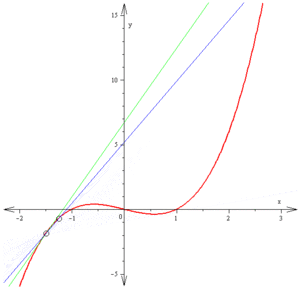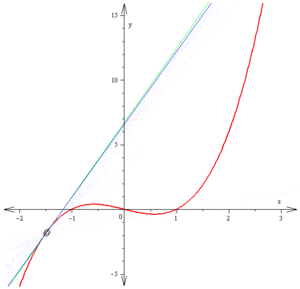
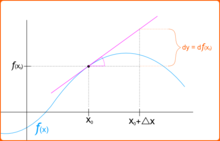
。 彷彿在用著可以調整『放大倍率』的『顯微鏡』逐步『觀入』 zoom in 一個『函數』,隨著『解析度』的提高,函數之『曲率』逐漸減小,越來越『逼近』一條『直線』── 某點的切線 ── 的啊!!
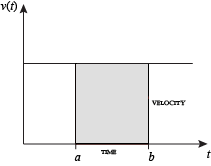
同樣的『積分』就像是『里程表』的『累計』一樣,可以用
![]()
來表示的呀!!