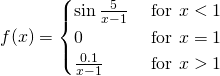《易緯略義》
乾鑿度曰:文王因陰陽定消息,立乾坤統天地,夫有形者生於無形,則乾坤安從生?故曰有太易、有太初、有太始、有太素,太易者未見氣,太初者氣之始,太始者形之始,太素者質之始,氣形質具而未相離,故曰渾淪,言萬物相渾淪而未相離,視之不見、聽之不聞、循之不得、故曰易也, 易無形埒也。易變而為一,一變而為七,七變而為九,九者氣變之究也,乃復變而為一,一者形變之始,清輕上為天,濁重下為地,物有始有壯有究,故三畫而成 乾,乾坤相並俱生,物有陰陽,因而重之,故六畫而成卦。卦者挂也挂萬物視而見之故三畫已上。為地四畫已上為天物感以動類相應也陽氣從下生。動於地之下則應 於天之下動於地之中則應於天之中動於地之上則應於天之上。故初以四,二以五,三以上。此謂之應陽動而進,陰動而退,故陽以七,陰以八,為彖,易一陰一陽合而為十五,之謂道。陽變七之九陰變八之六合於十五則彖變之數若。陽動而進變七之九象其氣之息也陰動而退變八之六象其氣之消也故太一取其數以行九宮四正四維皆合於十五。五音六律七宿。由此作焉。故大衍之數五十所以成變化而行鬼神也。日十干者五音也。辰十二者六律也。星二十八者七宿也。凡五十所以大閡物而出之者也。此原七八九六之始一陰一陽之位說詳虞氏消息。
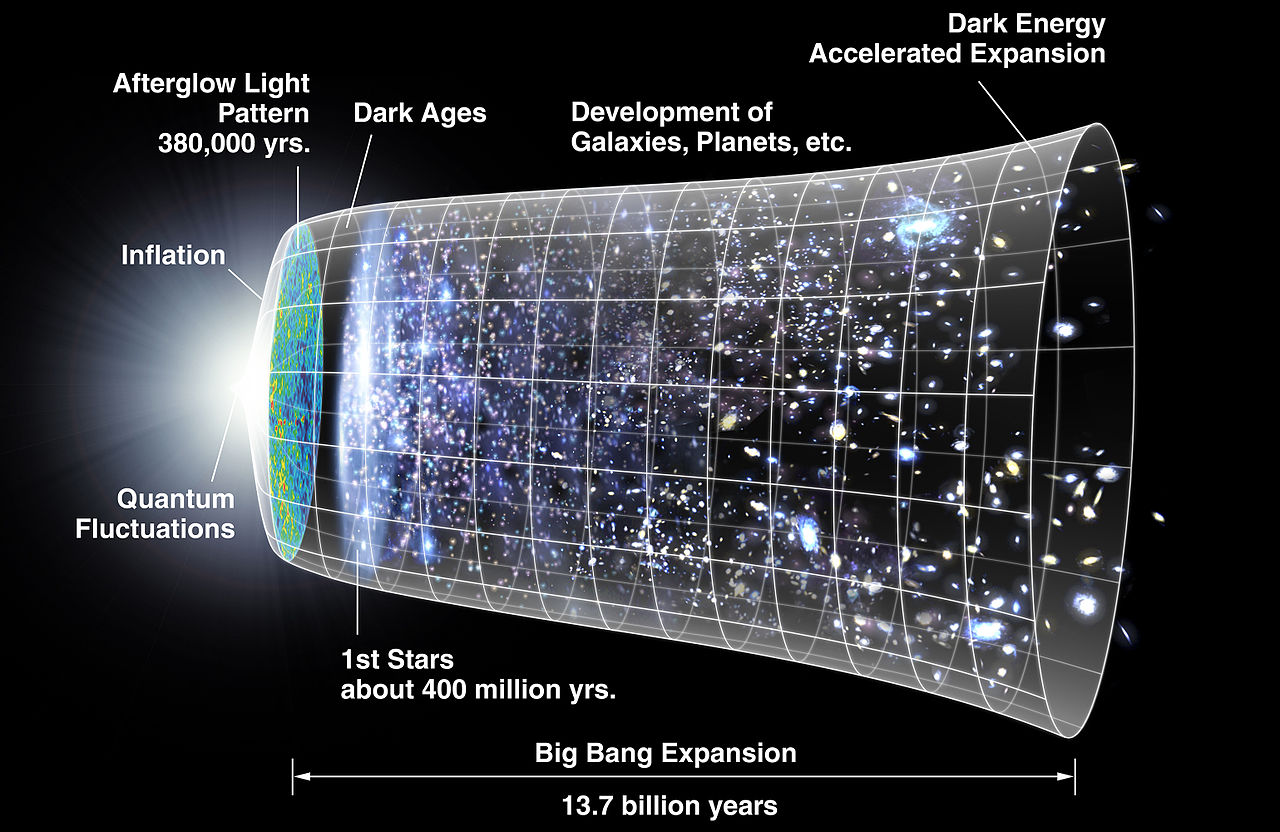
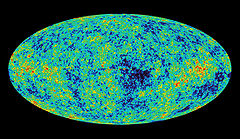
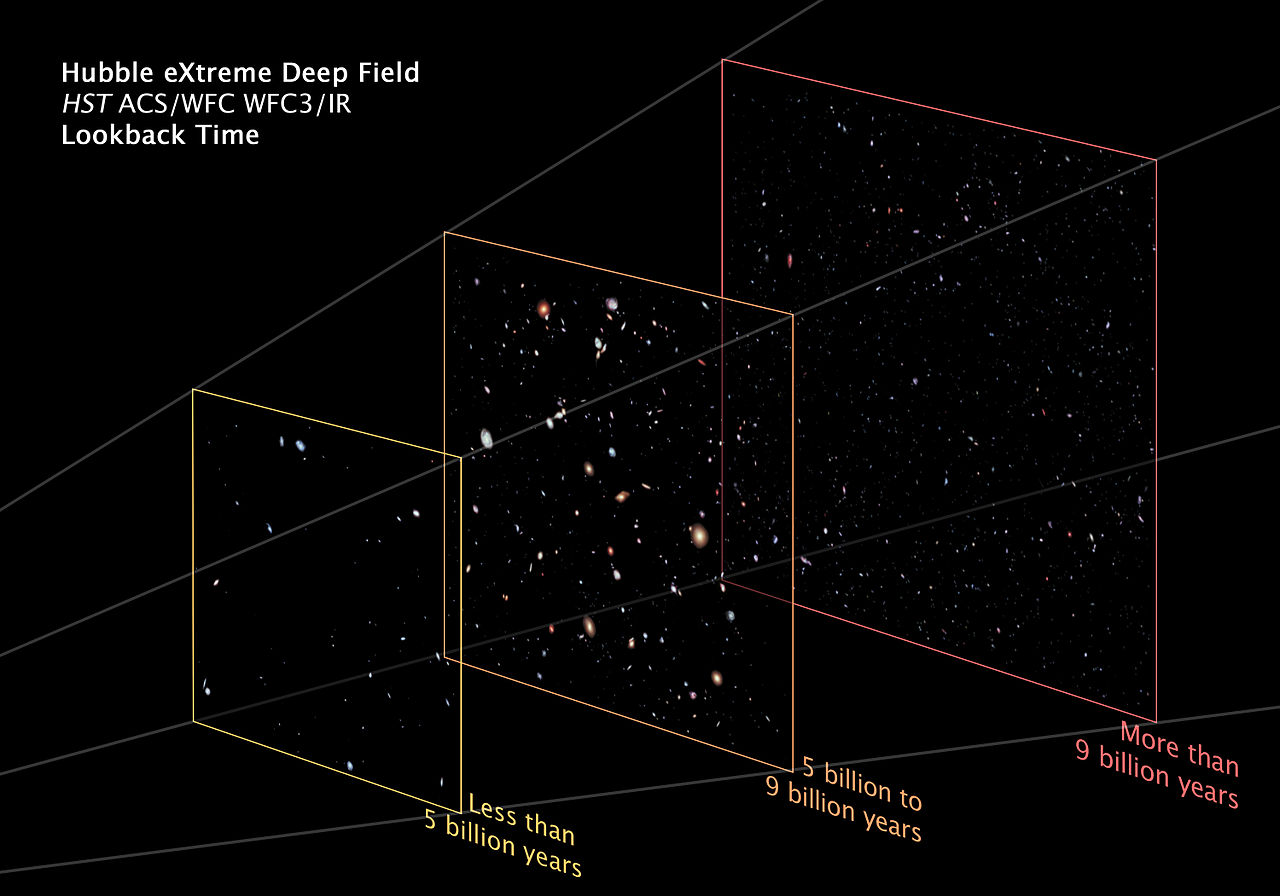
『大爆炸』Big Bang 又稱『大霹靂』,描述宇宙誕生『初始條件』及其『後續演化』的模型,這個模型得到了現今科研和觀測廣泛的支持。宇宙學家一般所說的大爆炸是:宇宙在遙遠的過去,由一個密度極大而且溫度極高的『太初狀態』演變而來的。依據二零一三年普朗克衛星所得到的最佳觀測結果,這個大爆炸距今約為 ![]() 億年前,並且一直不斷的膨脹來到了今天的狀態。一九二二年蘇聯物理學家『亞歷山大‧亞歷山大洛維奇‧弗里德曼』 Александр Александрович Фридман 用廣義相對論描述了流體,從而給出了這一模型的場方程式。一九二九年美國物理學家『愛德溫‧哈伯』通過觀測發現,從地球到達遙遠星系的距離正比於這些星系的『紅位移』 red shift,從而得出了『膨脹宇宙』的觀點。據聞『大爆炸』一詞首先是由英國著名天文學家弗雷德‧霍伊爾爵士 Sir Fred Hoyle 在一九四九年三月 BBC 的一次廣播節目中將『那個理論』稱作『這個大爆炸的觀點』。由於霍伊爾是宇宙『穩態學說』的倡導者,因此許多通俗軼事記載霍伊爾這樣講是出於諷刺,但是霍伊爾本人明確的否認了這一點,他聲稱這只是為了強調這兩種模型的顯著不同之處。
億年前,並且一直不斷的膨脹來到了今天的狀態。一九二二年蘇聯物理學家『亞歷山大‧亞歷山大洛維奇‧弗里德曼』 Александр Александрович Фридман 用廣義相對論描述了流體,從而給出了這一模型的場方程式。一九二九年美國物理學家『愛德溫‧哈伯』通過觀測發現,從地球到達遙遠星系的距離正比於這些星系的『紅位移』 red shift,從而得出了『膨脹宇宙』的觀點。據聞『大爆炸』一詞首先是由英國著名天文學家弗雷德‧霍伊爾爵士 Sir Fred Hoyle 在一九四九年三月 BBC 的一次廣播節目中將『那個理論』稱作『這個大爆炸的觀點』。由於霍伊爾是宇宙『穩態學說』的倡導者,因此許多通俗軼事記載霍伊爾這樣講是出於諷刺,但是霍伊爾本人明確的否認了這一點,他聲稱這只是為了強調這兩種模型的顯著不同之處。
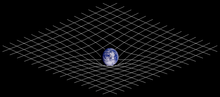
『時空』竟然有一個『起源』,那麼到底又該如何想像的呢??
真的能求解 ![]() 太易之波函數??
太易之波函數??
英國著名物理學家史蒂芬‧威廉‧霍金 Stephen William Hawking 患有肌肉萎縮性側索硬化症,全身癱瘓不能發音,窮其畢生精力研究『黑洞』 black hole 。一九八八年時寫了一本《時間簡史》的科普圖書︰講述關於宇宙的起源和命運,介紹了什麼是宇宙、宇宙發展的現狀以及關於宇宙本性的前沿知識,解釋了黑洞和大爆炸等等天文物理學的理論。
在《時間簡史》一書裡,據霍金自己說︰一九七五年,他與美國理論物理家『基普‧索恩』 Kip Stephen Thorne 打賭『黑洞到底存不存在?』,為什麼打賭呢?也許霍金擔心黑洞只是『理論』上的概念,而於『現實』中可能根本不存在。或許霍金是『巴斯卡論證』的信徒,他很有意思的押寶在黑洞不存在上。也許霍金想即使他『萬一』輸了,雖然得『贈送』索恩情色雜誌《閣樓》 Penthouse 一年,畢竟證明他是『對的』。假使『幸運』贏了,就算終究他是『錯的』,至少『贏得』專門踼爆英國皇室醜聞的《私家偵探》 Private Eye 雜誌四年。事實上不久之後,霍金就很『⊙⊙』的認輸了。一九九零年霍金到南加州大學演講,當時索恩人在莫斯科,於是霍金大張旗鼓闖入索恩的辦公室拿出當年的賭據來按手印『認輸』。據聞這件事情還有個很好玩的結局,霍金就給索恩訂閱了一年的《閣樓》雜誌,這可讓『索恩的妻子』很惱火,原因倒不是因為對『閣樓』的『內容反感』,因為他的妻子認為霍金應該訂閱一份對『男女都適合』的刊物。
連光線都逃脫不了的黑洞,它可以吞天噬地,是巨大恆星的墳塚。它是因為在核融合反應的燃料耗盡後,發生重力塌縮所形成的。就目前所知,質量最小的黑洞大約是太陽質量三點八倍!!
黑洞的存在,使人們必須面對數學上的『奇異點』 singularity,又叫做『奇點』 ── 該點的值是無限大 ![]() ──,由於傳統數學中『無限大』的『巨量』
──,由於傳統數學中『無限大』的『巨量』 ![]() 就是計算機學中的『非數』 NaN Not a Number,以至於很難直接的處理。就像光滑的曲線或平面上如果有一個突起來的點,就會破壞了函數在那一點的『可微分性』。或是講一條連續的曲線中有一個斷掉的點,這個點就破壞了這條曲線的『連續性』一樣。只是『物理方程式』既然描述『大自然現象』,人們就得『解釋』這些『奇異點』的『性質』,或許創造新的『算術理論』,避開『邏輯矛盾』的啊!!
就是計算機學中的『非數』 NaN Not a Number,以至於很難直接的處理。就像光滑的曲線或平面上如果有一個突起來的點,就會破壞了函數在那一點的『可微分性』。或是講一條連續的曲線中有一個斷掉的點,這個點就破壞了這條曲線的『連續性』一樣。只是『物理方程式』既然描述『大自然現象』,人們就得『解釋』這些『奇異點』的『性質』,或許創造新的『算術理論』,避開『邏輯矛盾』的啊!!
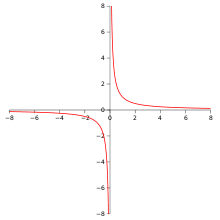
舉例來說,雙曲函數 ![]() 在
在 ![]() 實是『未定義』的
實是『未定義』的 ![]() ,當
,當 ![]() 是『正無窮小』
是『正無窮小』 ![]() 時,
時, ![]() ,於
,於 ![]() 是『負無窮小』時,
是『負無窮小』時, ![]() ,此處
,此處 ![]() 是『超實數』中的『巨量』,也就是指『無限大』數。也就是說這個函數在
是『超實數』中的『巨量』,也就是指『無限大』數。也就是說這個函數在 ![]() 時有一個『奇點』。假使我們考慮一個『生長方程式』
時有一個『奇點』。假使我們考慮一個『生長方程式』
![]()
,這個方程是的解是
![]()
,當 ![]() 時,
時,![]() 。這個方程式或想描述某些自然界的『臨界現象』 ,彷彿像核子之『連鎖反應』一般發生了突然的『大量增生』現象,那該如何『了解』這個『無限大』之『意義』的呢??
。這個方程式或想描述某些自然界的『臨界現象』 ,彷彿像核子之『連鎖反應』一般發生了突然的『大量增生』現象,那該如何『了解』這個『無限大』之『意義』的呢??
如果說設想 ![]() ,這樣是『合理』的嗎??
,這樣是『合理』的嗎??
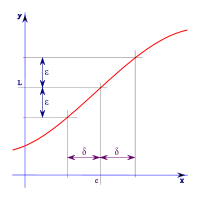
那麼在『超實數系』中又是怎麽看待『極限』的呢?假使說『一個點』代表一個『實數』 ![]() ,這樣所對應的『超實數』
,這樣所對應的『超實數』 ![]() 中的『無窮小』數就是指『那個實數』的『鄰域』。從『包含』與『不包含』這個點
中的『無窮小』數就是指『那個實數』的『鄰域』。從『包含』與『不包含』這個點 ![]() 上來講,可以區分出『兩種鄰域』,能夠得出『不包含』這個點之『三種極限定義』
上來講,可以區分出『兩種鄰域』,能夠得出『不包含』這個點之『三種極限定義』
一、只要 ![]() 且
且 ![]() ,就能得到
,就能得到 ![]() ,此時我們說
,此時我們說 ![]() 。
。
二、只要 ![]() 且
且 ![]() ,就能得到
,就能得到 ![]() ,此時我們說
,此時我們說 ![]() 。
。
三、只要 ![]() 且
且 ![]() ,就能得到
,就能得到 ![]() ,此時我們說
,此時我們說 ![]() 。
。
為什麼用『不包含這個點』來作論述的呢?這是因為一個函數在『某個點』未必有『定義』或者說未必能夠『定義』的ㄡ!假使這個 函數在此點 ![]() 是『連續的』,那麼必然是
是『連續的』,那麼必然是 ![]() 的啊!
的啊!
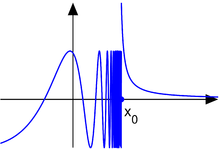
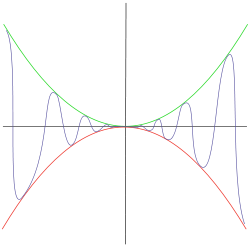
比方講,左圖的函數在 ![]() 時,又怎麽可能是連續的呢?
時,又怎麽可能是連續的呢? ![]() 、
、 ![]() 而且
而且 ![]() ,所以才說在『此點』這一個函數之『極限值』是不存在的啊!!
,所以才說在『此點』這一個函數之『極限值』是不存在的啊!!
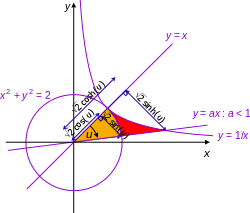
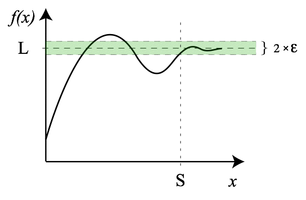
然而左圖又是表述什麼狀況的呢?即使我們不考慮各種『可能狀況』 ,未必就是說不可以『直覺』的『推導』出下面的結果
![]()
![]()
。這樣如果我們想要求得某數之『天圓 ○ 之極』,假使我們已經知道總是 ![]() ,而且當在『此極限』 之時
,而且當在『此極限』 之時 ![]() 的話,那麼我們『當不當』同意,這個『 ○ 之極』也趨近『同一極限』的呢?這就叫做『夾擊定理』或稱之為『三明治法則』,如此人們自然的就將
的話,那麼我們『當不當』同意,這個『 ○ 之極』也趨近『同一極限』的呢?這就叫做『夾擊定理』或稱之為『三明治法則』,如此人們自然的就將 ![]() 看成
看成 ![]() 之數,這樣
之數,這樣 ![]() 之結果難道不應該是個『零』的嗎?也就是說,就算有了『無窮小』、『無限大』以及『極限法則』以後,『如何計算』的問題依然存在的啊?也許正因為如此,有些數學家認為『無窮小』數的說法並沒有什麼『特別的』益處,也還是需要『創造解答』的方案罷了。即使這樣的『批評指正』自有所指,然而在『科學實驗』裡,所有的『量測』也都只有『有限』之『精準度』,或許僅用『有理數』來表達就『足夠』的了ㄚ?那所謂『實數』與物理『連續體』豈不也是多餘的呢??
之結果難道不應該是個『零』的嗎?也就是說,就算有了『無窮小』、『無限大』以及『極限法則』以後,『如何計算』的問題依然存在的啊?也許正因為如此,有些數學家認為『無窮小』數的說法並沒有什麼『特別的』益處,也還是需要『創造解答』的方案罷了。即使這樣的『批評指正』自有所指,然而在『科學實驗』裡,所有的『量測』也都只有『有限』之『精準度』,或許僅用『有理數』來表達就『足夠』的了ㄚ?那所謂『實數』與物理『連續體』豈不也是多餘的呢??
── 理想或是近似,到底是誰帶來了無限大的勒!! ──