樹莓派、樹莓派之學習、樹莓派之教育

【Sonic π】電聲學之電路學《四》之《 V!》‧下

十二因緣

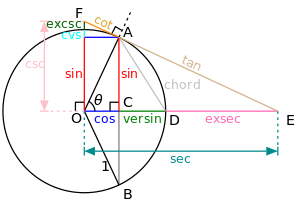
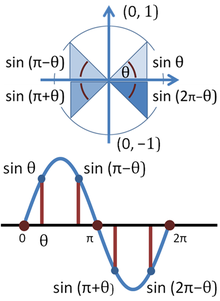
《緣起經》玄奘譯

佛言，云何名緣起初義？謂：依此有故彼有，此生故彼生。所謂：無明緣行，行緣識，識緣名色，名色緣六處，六處緣觸，觸緣受，受緣愛，愛緣取，取緣有，有緣生，生緣老死，起愁、歎、苦、憂、惱，是名為純大苦蘊集，如是名為緣起初義。

『邏輯學』上說『有□則有○，無○則無□』，既已『有□』又想『無○』，哪裡能夠不矛盾的啊！過去魏晉時『王弼』講︰一，數之始而物之極也。謂之為妙有者，欲言有，不見其形，則非有，故謂之妙；欲言其無，物由之以生，則非無，故謂之有也。斯乃無中之有，謂之妙有也。假使用『恆等式』 1 - x^n = (1 - x)(1 + x + \cdots + x^{n-1}) 來計算 \frac{1 + x + \cdots + x^{m-1}}{1 + x + \cdots + x^{n-1}}，將等於 \frac{1 - x^m}{1 - x^n} = (1 - x^m) \left[1 + (x^n) + { (x^n) }^2 + { (x^n) } ^3 + \cdots \right] = 1 - x^m + x^n - x^{n+m} + x^{2n} - \cdots，那麼 1 - 1 + 1 - 1 + \cdots 難道不應該『等於』 \frac{m}{n} 的嗎？一七四三年時，『伯努利』正因此而反對『歐拉』所講的『可加性』說法，『同』一個級數怎麼可能有『不同』的『和』的呢？？作者不知如果在太空裡，乘坐著『加速度』是 g 的太空船，在上面用著『樹莓派』控制的『奈米手』來擲『骰子』，是否一定能得到『相同點數』呢？難道說『牛頓力學』不是只要『初始態』是『相同』的話，那個『骰子』的『軌跡』必然就是『一樣』的嗎？？據聞，法國籍義大利裔大數學家『約瑟夫‧拉格朗日』伯爵 Joseph Lagrange 倒是有個『說法』︰事實上，對於『不同』的 m,n 來講， 從『幂級數』來看，那個 = 1 - x^m + x^n - x^{n+m} + x^{2n} - \cdots 是有『零的間隙』的 1 + 0 + 0 + \cdots - 1 + 0 + 0 + \cdots，這就與 1 - 1 + 1 - 1 + \cdots 『形式』上『不同』，我們怎麼能『先驗』的『期望』結果會是『相同』的呢！！

假使我們將『幾何級數』 1 + z + z^2 + \cdots + z^n + \cdots = \frac{1}{1 - z} ，擺放到『複數平面』之『單位圓』上來『研究』，輔之以『歐拉公式』 z = e^{i \theta} = \cos \theta + i\sin \theta，或許可以略探『可加性』理論的『意指』。當 0 < \theta < 2 \pi 時，\cos \theta \neq 1 ，雖然 |e^{i \theta}| = 1，我們假設那個『幾何級數』會收斂，於是得到 1 + e^{i \theta} + e^{2i \theta} + \cdots = \frac{1}{1 - e^{i \theta}} = \frac{1}{2} + \frac{1}{2} i \cot \frac{\theta}{2}，所以 \frac{1}{2} + \cos{\theta} + \cos{2\theta} + \cos{3\theta} + \cdots = 0 以及 \sin{\theta} + \sin{2\theta} + \sin{3\theta} + \cdots = \frac{1}{2} \cot \frac{\theta}{2}。如果我們用 \theta = \phi + \pi 來『代換』，此時 -\pi < \phi < \pi，可以得到【一】 \frac{1}{2} - \cos{\phi} + \cos{2\phi} - \cos{3\phi} + \cdots = 0 和【二】 \sin{\phi} - \sin{2\phi} + \sin{3\phi} - \cdots = \frac{1}{2} \tan \frac{\phi}{2}。要是在【一】式中將 \phi 設為『零』的話，我們依然會有 1 - 1 + 1 - 1 + \cdots = \frac{1}{2} ；要是驗之以【二】式，當 \phi = \frac{\pi}{2} 時，原式可以寫成 1 - 0 - 1 - 0 + 1 - 0 - 1 - 0 + \cdots = \frac{1}{2}。如此看來 s = 1 + z + z^2 + z^3 + \cdots = 1 +z s 的『形式運算』，可能是有更深層的『關聯性』的吧！！

Circle-trig6.svg

複數平面之單位圓

300px-Unit_circle_angles_color.svg

220px-Periodic_sine

假使我們將【二】式對 \phi 作『逐項微分』得到 \cos{\phi} - 2\cos{2\phi} + 3\cos{3\phi} - \cdots = \frac{1}{4} \frac{1}{{(\cos \frac{\phi}{2})}^2}，此時令 \phi = 0，就得到 1 - 2 + 3 - 4 + 5 - \cdots = \frac{1}{4}。如果把【一】式改寫成 \cos{\phi} - \cos{2\phi} + \cos{3\phi} - \cdots = \frac{1}{2} 然後對 \phi 作『逐項積分』 \int \limits_{0}^{\theta} ，並將變數 \theta 改回 \phi 後得到 \sin{\phi} - \frac{\sin{2\phi}}{2} + \frac{\sin{3\phi}}{3} - \cdots = \frac{\phi}{2}；再做一次 作『逐項積分』 \int \limits_{0}^{\theta} ，且將變數 \theta 改回 \phi 後將得到 1 - \cos{\phi} - \frac{1 - \cos{2\phi}}{2^2} + \frac{1 - \cos{3\phi}}{3^2} - \cdots = \frac{\phi^2}{4}，於是當 \phi = \pi 時，1 + \frac{1}{3^2} + \frac{1}{5^2} + \cdots = \frac{\pi^2}{8}。然而 1 + \frac{1}{3^2} + \frac{1}{5^2} + \cdots = [1 + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \frac{1}{5^2} + \cdots] - [\frac{1}{2^2} + \frac{1}{4^2} + \frac{1}{6^2} + \cdots] =[1 - \frac{1}{4}][1 + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \frac{1}{5^2} + \cdots] ，如此我們就能得到了『巴塞爾問題』的答案 \sum \limits_{n=1}^{\infty}\frac{1}{n^2} = \frac{\pi^2}{6}。那麼

S= \ \ 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + \cdots 減
4S=\ \ \ \ \ \ 4 + \ \ \ \ \ 8 + \ \ \ \ \ 12 + \cdots 等於
-3S= 1 - 2 + 3 - 4 + 5 - 6 + \cdots = \frac{1}{4}，所以 S = - \frac{1}{12}。

但是這樣的作法果真是有『道理』的嗎？假使按造『級數的極限』 之『定義』，如果『部份和』 S_n = \sum \limits_{k=0}^{n} a_n 之『極限』 S = \lim \limits_{n \to \infty} S_n 存在， S 能不滿足 S = a_0 + a_1 + a_2 + a_3 + \cdots = a_0 + (S - a_0) 的嗎？或者可以是 \sum \limits_{n=0}^{\infty} k \cdot a_n \neq k \cdot S 的呢？即使又已知 S^{\prime} = \sum \limits_{n=0}^{\infty} b_n ，還是說可能會發生 \sum \limits_{n=0}^{\infty} a_n + b_n \neq S + S^{\prime} 的哩！若是說那些都不會發生，所謂的『可加性』的『概念』應當就可以看成『擴大』且包含『舊有』的『級數的極限』 的『觀點』的吧！也許我們應當使用別種『記號法』來『表達』它，以免像直接寫作 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + \cdots = - \frac{1}{12} 般的容易引起『誤解』，畢竟是也存在著多種『可加法』的啊！至於說那些『可加法』的『意義詮釋』，就看『使用者』的吧！！

在此僅略為補充，『複數函數』 f(z) = \frac{1}{1 -z} 除了 z = 1 是『不連續』外，而『幾何級數』 1 + z + z^2 + \cdots + z^n + \cdots = \frac{1}{1 - z}  在 |z| < 1 『都收斂』，因是 \lim \limits_{z \to |z_1^{-}| = 1^{-}} 1 + z + z^2 + \cdots + z^n + \cdots = f(z_1)。也就是說『連續性』、『泰勒展開式』與『級數求和』等等之間有極深的『聯繫』，事實上它也與『定點理論』 f(x) = x 之『關係』微妙的很啊！！

220px-Casimir_plates_bubbles.svg

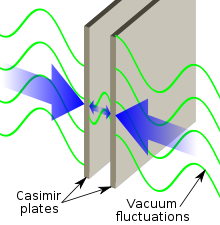
220px-Casimir_plates.svg

220px--Water_wave_analogue_of_Casimir_effect.ogv

一九四八年時，荷蘭物理學家『亨德里克‧卡西米爾』 Hendrik Casimir 提出了『真空不空』的『議論』。因為依據『量子場論』，『真空』也得有『最低能階』，因此『真空能量』不論因不因其『實虛』粒子之『生滅』，總得有一個『量子態』。由於已知『原子』與『分子』的『主要結合力』是『電磁力』，那麼該『如何』說『真空』之『量化』與『物質』的『實際』是怎麽來『配合』的呢？因此他『計算』了這個『可能效應』之『大小』，然而無論是哪種『震盪』所引起的，他總是得要面臨『無窮共振態』 \langle E \rangle = \frac{1}{2} \sum \limits_{n}^{\infty} E_n 的『問題』，這也就是說『平均』有『多少』各種能量的『光子？』所參與 h\nu + 2h\nu + 3h\nu + \cdots 的『問題』？據知『卡西米爾』用『歐拉』等之『可加法』，得到了 {F_c \over A} = -\frac {\hbar c \pi^2} {240 a^4}。

此處之『負』 - 代表『吸引力』，而今早也已經『證實』的了，真不知『宇宙』是果真先就有『計畫』的嗎？還是說『人們』自己還在『幻想』的呢？？