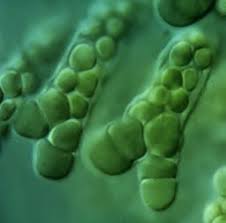
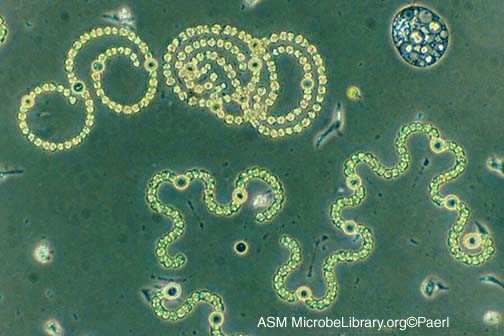
一九六八年荷蘭 Utrecht 大學的生物學和植物學家，匈牙利裔的林登麥伊爾 Aristid Lindenmayer 研究多種類型的海藻 ── 例如藍綠項圈藻 ── 的生長模式，提出了有關生長發展中的細胞交互作用的數學模型 ── Lindenmayer 系統，簡稱作 L 系統 ──，用於表達簡單多細胞生物體生長的『正則』regular 描述，並且試圖證明它與植物細胞之間的緊密關係。之後『 L 系統』 被廣泛的應用於『植物生長過程』之研究，然後又被擴展成能夠描述高等植物及其複雜枝杈結構。L 系統內『自然遞迴』的規則產生了『自相似性』，因此也可以用來簡易的描述像分形 fractal 的這一類事物。同樣的植物模型與看起來自然之有機構造可以用它簡易的定義，藉著增加遞迴層次，慢慢的『生長』變得越來越『複雜』。因是之故，它也常被用於『人造生命』artificial life 的『製造』軟體。
其實 L 系統非常的類似 semi-Thue 之字串改寫系統，其中最主要的『差異』在於它是『同時的』或說『並行的』應用『所有可用』之『生產規則』，可以定義如下︰
系統是一個有序三元組 
，其中
是可被改寫的字詞符號集合，有時又稱作『變數』，
是改寫系統的『初始字串』，又叫做『公理』axiom 或『起始者』initiator，
是『生產規則』，其中可以包含一些未列在 內的『常數符號』── 相對於變數，指不可被改寫取代者 ──，還有著一種『約定』，任何 中的變數 
假使沒有生產規則的定義，意味著『 
』。
，
舉例而言，如果使用 L 系統定義『某物』︰
變數︰『0』，『1』
常數︰『 [』，『]』
公理︰0
規則︰
1→11
0→1[0]0
當然我們可以推導出此物的『演變』︰
起始︰0
第一次遞迴︰1[0]0
第二次遞迴︰11[1[0]0]1[0]0
第三次遞迴︰1111[11[1[0]0]1[0]0]11[1[0]0]1[0]0
…
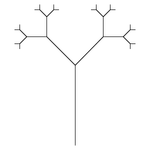
假使我們使用 Logo 語言的『海龜』 turtle 繪圖法，定義了︰
0︰畫一節帶葉子的線
1︰畫一根枝幹的線段
[︰將目前海龜的狀態── 所在位置和朝向角度 ──存上堆疊，然後向左轉 45 度
]︰從堆疊頂端取回海龜的狀態，然後向右轉 45 度
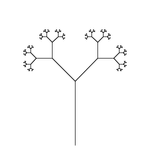
左圖就是這一隻海龜演示著此物之第【幾】次演變的尾巴軌跡︰剛起始【0】、第一次【1】、第二次【2】、第三次【3】、第四次【4】和第七次【7】。
當然上一篇裡的『科赫雪花』也可以用這樣的對應方式畫出它的圖形來，你只需要決定那個『F』是『向前』多少就可以的了！
子曰：
不憤不啟，不悱不發，舉一隅不以三隅反，則不復也。
也許是想講許多的事理都是相通的吧！！
偶而人們會發覺用著『不同之語言』表達『相同的概念』時，它們的『難易度』可能會落差很大。事實上這也許是許多『特定領域語言』DSL Domain-specific language 之所以興起的道理。它的主要目的並不是為著『一般性』語言的考量，而是追求在那個特定領域中之表達的『方便性』以及陳述的『涵蓋性』。或許古人所謂的『觸類能旁通』和『不自以為是』之態度才是最好的『學習之路』的吧！！
─── 向左轉或者往右彎，是否一直是個問題的呢？ ───
Stands back from the keyboard in ametmaenz! Thanks!