【Sonic π】電聲學之電路學《一》中

Pure logical thinking cannot yield us any knowledge of the empirical world; all knowledge starts from experience and ends in it. Propositions arrived at by purely logical means are completely empty as regards reality.

Einstein 1933

一個物理系統『因次分析』的重要性並不在於『答案求解』，而是在於『因次分析』的核心概念是『相似性』 Similarity。於是將我們帶進了一個雖然是由不同『事物』所產生『物理現象』的世界，然而在這個世界裡，這些『物理現象』彼此間卻有著『等效性』Equivalence 的描述。不知一個玩著等比例『模型飛機』的人，是否曾經想像過在『某種條件』下，它與它的『本尊』── 那架真實的飛機 ── 的『氣體動力學』方程式是『相似的』，而且它在『風洞』實驗的模擬中也可用來研究飛行的！那麼我們要如何知道，這個『某種條件』是哪種條件的呢？如果就數學上來講，通常一個表達式之所以會作『變數轉換』，為的是得到更『簡潔化約』的『對等的』表達式。假使這個『數學表達式』描述的就是那架『模型飛機的方程式』，我們能夠知道『什麼轉換』可以得到『最簡』方程式的嗎？『因次分析』正是這兩個問題的『藥方』，是『求解答案』前的『問題簡化』！！假使我們能夠得到比較簡單的問題，那麼又為什麼不會這麼作的呢？？

熱力學第一定律
能量守恆定律的創立者
能量的單位是焦耳

熱力學之父
卡諾熱機與卡諾循環

可逆過程的提出者

一八四一年，英國物理學家詹姆斯‧普雷斯科特‧焦耳 James Prescott Joule 開始研究『電阻加熱』現象，他將一段導線浸入定量的水中，然後量測上升的溫度，在實驗過各種材質的導體、多種電流大小與不同時間長短後發現
$Q = I^2 \cdot R \cdot t$
，此處 $Q$ 是熱量【焦耳】、 $I$ 是電流量【安培】、 $R$ 是電阻值【歐姆】、 $t$ 時間【秒】。

之後焦耳啟始了『熱功當量』The mechanical equivalent of heat 的研究，一八四三年他說
wherever mechanical force is expended, an exact equivalent of heat is always obtained. ─── J.P. Joule, August, 1843

。所謂的熱功當量是指熱力學的單位『卡』與力學上『功』的單位『焦耳』之間存在的一種當量關係，因為用傳導熱量或者作功的方法都能改變物質系統的能量，所以他們的單位之間存在著一定換算關係。現今量測值是 1 cal = 4.186 J。一八四三年，焦耳在科克召開的英國科學協會的一次會議裡宣布了他的結果，迎來的卻是一片沉默。儘管遭受到冷遇，焦耳還是不屈不饒的尋找一種純機械的方式來顯示功和熱之間的轉化。之後，他測量了壓縮空氣所產生的熱量，此時他的文章甚至還被皇家學會拒絕，被迫不得不改在《哲學雜誌》上發表。在這篇文章中，焦耳直截了當地拋棄了，法國物理學家尼古拉‧萊昂納爾‧薩迪‧卡諾 Nicolas Léonard Sadi Carnot 與伯諾瓦‧保羅‧埃米爾‧克拉佩龍 Benoît Paul Émile Clapeyron 的『熱質說』，神懺式的寫下了︰

我認為這個理論……違反了被認可的哲學原則。因為它會得出『活力』 ── vis viva，代表能量 ── 可能會因實驗裝置的不正確設置而被銷毀的結論。因此，克拉佩龍先生得出推論，『當火焰的溫度比鍋爐高 1000°C 到 2000°C 時，熱量從火爐向鍋爐傳遞時會損失大量的活力。』因為堅信毀滅的力量是只屬於造物主的，我斷言……任何理論，如果在提出時要求了湮滅的力量，就肯定是錯誤的。

直到一八四五年，焦耳方在英國協會於劍橋舉辦的會議上宣讀了他的論文『論熱功當量』。在這篇論文中，焦耳闡述了他的最著名實驗︰透過重物下落時的所作的機械功，來轉動一個放置於隔熱水桶中之帶槳的轉輪，轉輪轉動會使水溫升高。藉此焦耳測得的熱功當量是每卡 4.41 焦耳。於一八五零年，焦耳又發表了一個修正的測量值，4.159J / cal，等於英制的 772.692 ft·lbf / Btu。

一八八九年十月十一日，焦耳在塞爾的家中逝世，被埋葬在該市的布魯克蘭公墓。在他的墓碑上刻有數字『772.55』，這是他在一八七八年的關鍵測量中得到的熱功當量值。墓碑上還刻有約翰福音的一段話，『趁著白日，我們必須做那差我來者的工；黑夜將到，就沒有人能做工了。【9：4】』

當人們在自然中的發現了一些『經驗定律』，有時並不代表我們『知道』它的『成因』。從科學史來看，許多的『物理概念』都是逐步建立起來的。『熱力學第一定律』是『能量守恆』定律對『非孤立系統』的擴展。此時能量可以用『功』 $W$ 或『熱』 $Q$ 的形式傳入或傳出系統。即：

$\qquad \mathrm \Delta E_{\rm int}= Q + W$

此處 $\Delta E_{\rm int}$ 為『系統內能』的變化量，如果外界對此系統做功，則 $W$ 取正值，反之為取負值。

對於『準靜態』的『可逆過程』，可以寫成微分形式

$\qquad \mathrm dE_{\rm int} = \delta Q + \delta W$

。一直要到『統計力學』之後，人們才能夠用『微觀粒子』間的『交互作用』來說明這些『現象』的『經驗定律』之『成因』。

假使將『電磁學』與『動力學』聯合起來看，『勞侖茲力定律』Lorentz force law 就十分重要。這個定律是一個『基本公理』，並不能夠從別的理論推導出來，而是由無數次『重複的實驗』所得到之結果。在『電動力學』裡，『勞侖茲力』是一個『帶電粒子』於電磁場中運動時，所感受到的電磁作用力。可以用方程式表達為

$\mathbf{F} = q (\mathbf{E} +\mathbf{v} \times \mathbf{B})$

此處， $\mathbf{F}$ 是『勞侖茲力』， $q$ 是帶電粒子的『電荷量』， $\mathbf{E}$ 是『電場』， $\mathbf{v}$ 是帶電粒子的『速度』， $\mathbf{B}$ 是『磁場』。

之前我們談到過《德汝德模型》，那麼是否可以用它來解釋『焦耳定律』的呢？回顧前文，德汝德將『導體』想像成由相對固定的『正離子』與可移動的『自由電子』所構成。這些為數眾多的『自由電子』彼此間不斷的發生『碰撞』，又和固定的『正離子』間也發生碰撞。同時德汝德假設了︰

一、如果沒有外部的『電磁場』作用，『自由電子』將會作『直線運動』，彼此間的『電磁作用力』可以被忽略。這意味著是一種『獨立電子』的假設，它處於一個由『正離子』與『其他電子』所構成的『平均的環境』 ── 因此淨作用為零 ──，統計上來講這一般認為是『合宜的』。

二、『電子』和『正離子』之間的『碰撞』是『即時』的，統計上無關之『隨機事件』，所以總體來說這沒有任何『淨貢獻』，雖然有不同的學者『批評』它的『合宜性』。然而如果從『散射事件』來看，這也許只是說某些『物質屬性』之『均向性』的另一種說法罷了。

三、假設了『平均碰撞時間』 $\tau$ 的『存在』，所以我們可以說很小的一段時距 $\delta t$ 發生『碰撞』的『機會』是 $\frac {\delta t}{\tau}$ ，而且這個『機率』和一個『自由電子』的『位置』與『動量』無關。這正像是『丟一根』長度為 $\delta t$ 的『針』投到一個以 $\tau$ 為『格子線』板子上，問『針』掉到『線上』的『機率』大小如何，通常被認為是很好的『近似』。

四、『碰撞』後的『熱電子』應該保有該處『熱平衡』的速度。這是一個作用『鄰近原則』的假設，一般從『物理因果』上講，以為應是『正確的』。

事實在『假設二』中的『電子』與『正離子』的『散射碰撞』，是一種『能量不守恆』的碰撞，『電子』將部份的『能量』移轉給了『正離子』，並使得『金屬』溫度上升，這說明了『焦耳定律』的由來。依據『假設三』，一個電子在很小時距 $\delta t$ 發生碰撞的機率是 $P_c = \frac{\delta t}{\tau}$ ，那麼某個電子從一開始 $0$ 到 $t$ 時刻不發生碰撞的機率可以這樣計算︰將 $0$ 到 $t$ 時距切割成 $N$ 小段，每一段長 $\delta t$ ，如此 $t = N \delta t$ 。於是

$P_{nc}(t) = \lim \limits_{\delta t \rightarrow 0} \left( 1 - \frac{\delta t}{\tau} \right) \cdots \left( 1 - \frac{\delta t}{\tau} \right) = \lim \limits_{\delta t \rightarrow 0} {\left( 1 - \frac{\delta t}{\tau} \right)}^N$

$= \lim \limits_{\delta t \rightarrow 0} {\left( 1 - \frac{\delta t}{\tau} \right)}^{\frac{t}{\delta t} } = \lim \limits_{- \frac{\delta t}{\tau} \rightarrow 0} {\left[ {\left( 1 - \frac{\delta t}{\tau} \right)}^{- \frac{\tau}{\delta t}} \right]}^{- \frac{t}{\tau}} = e^{- t/ \tau}$

，如此 $P_{nc} \cdot P_c = e^{- t/ \tau} \frac{dt}{\tau}$ 就是間隔了 $t$ 時間， $t + dt$ 時發生碰撞的機率。

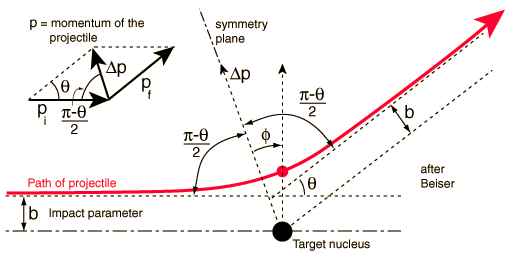
參考上圖，一個電子以『初始動量』 $\vec{p} = m \cdot \vec{v}$ 在電場 $\vec{E}$ 中作運動，並於 $t$ 時間後與正離子發生碰撞，在發生碰撞前，電子將以 $\vec{a} = \frac{\vec{E} e t}{m}$ 作加速，它的速度將會是 $\vec{v_i} = \vec{v} + \Delta \vec{v} = \vec{v} + \vec{a} t = \vec{v} + \frac{\vec{E} e t}{m}$ 。然後與正離子發生碰撞，依據『假設二』，這個『散射現象』是統計上無關的『隨機事件』，於是每一『立體角』Solid angle $d \Omega$ 方向的『散射機率』 $\frac{d \Omega}{4 \pi} = \sin(\theta) d \theta d \Phi / 4 \pi$ 都相等。再按造『假設四』，散射後的速度 $| \vec{v_f} | = | \vec{v} |$ ，這個 $v$ 就是電子的『熱速度』。因此這個電子移轉給正離子的能量是

$\Delta E(\theta, \Phi) = \frac{1}{2} m ({v_i}^2 - {v_f}^2) = \frac{1}{2} m ({v_i}^2 - v^2)$

$= \frac{1}{2} m [ ( v_2 + {\Delta v}^2 + 2 v \Delta v \cos{\theta} - v^2 ]$

$= \frac{{(e E t)}^2}{2 m} + v E e t \cos{\theta}$

。各方向的平均移轉能量為

$\Delta E = \int \frac{d \Omega}{4 \pi} \Delta E(\theta, \Phi)$

$= \frac{1}{4 \pi} \int_{0}^{ 2 \pi} d \Phi \int_{0}^{\pi} \sin(\theta) d \theta \Delta E(\theta, \Phi) = \frac{{(e E t)}^2}{2 m}$

。如果計之以 $P_c \cdot P_{nc}$ 的機率，如此每個電子每次碰撞，平均的能量損失是

$\langle \Delta E \rangle = \int_{0}^{\infty} \frac{d t}{\tau} e^{- t/ \tau} \Delta E = \int_{0}^{\infty} \frac{d t}{\tau} e^{- t/ \tau} \frac{{(e E t)}^2}{2 m} = \frac{{(e E \tau)}^2}{m}$