六個頂點之全部七十八種
朋友與陌生人 
圖
沒有此性質
友誼定理 Friendship Theorem 如是說：
在一群人數多於三的群體中，假使任意兩人都恰有一個共同認識的朋友，那麼這群人中定有一人是所有人都認識的。
設想六個人的一個聚會，其中任兩人要不是初次見面，就是已經認識，一個稱作『Theorem on friends and strangers』這麼講︰In any party of six people either at least three of them are (pairwise) mutual strangers or at least three of them are (pairwise) mutual acquaintances.
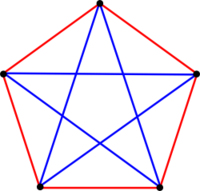
為了證明這個定理，讓我們用『圖論』graph theory 的語言來將其改寫。那六個人稱作六個『頂點』vertice ，任兩個『頂點』 edge 之間的連『邊』，代表兩人關係，『紅色』意味是『陌生人』，『藍色』標示是『朋友』。如是此圖裡，任兩『頂點』都會有一『色邊』連接，這十五條『邊』不是『紅色』就是『藍色』，這在『圖論』中叫做 『完全圖』。於是『朋友與陌生人定理』就被翻譯成了︰在一個 的完全圖內，假使每邊任意塗上紅或藍色，必然會產生一個紅色或藍色的三角形。
證明︰
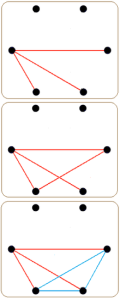
隨意選擇一個頂點 
，它可以有五條邊和其他頂點相連。由於只有兩種顏色，按照鴿巢原理，五條邊中至少有三條是同色的，就假設它是紅色的吧。也就是說 以這三條紅色的邊連接到另外的三個頂點 
，如果這三個頂點間有一條邊是紅色的，那麼就會產生了一個紅色三角形。除非這三條邊都是藍色的，但是此時就會有一個藍色三角形 的了。
『拉姆齊理論』說一個大的『有結構』物件的任意『分割』，總有一個『分割』保有那個『大結構』之『子結構』，雖然我們可以證明它的『存在性』，這個證明卻並未提供任何『建構』它的方法。因此一個夠大的看似『無序』的『集合』，常常可以『發現』某種『次序』在其中，讓人們訝異那可能是真的嗎！！這個『拉姆齊』生於劍橋，其父親是麥格達倫學院的校長，其弟麥可‧拉姆齊是第一百任坎特伯里大主教。他初於溫切斯特公學學習，後來進入劍橋大學三一學院學習數學。他的妻子說他是個『態度堅定的無神論者』。得年不到二十七歲的一生中，他涉獵了很多學術領域。據聞有一天，他和查爾斯‧凱‧奧格頓聊天時，說他想學德語。奧格頓便給了他一本文法書、字典和一篇艱澀的心理學論文並告訴他：『使用那本文法書和字典，告訴我們你的看法。』約一星期後，他不僅學會了德文，還對文法書中一些理論提出了反對意見。
一九二六年，拉姆齊發表了《Truth and Probability》論文，談論『信念』與『機率』的深層聯繫，並且提到了『賭博』中『賠率』和『賭注』的一種『簿記』 Book 之論。這就是現今稱之為『Dutch book』── 荷蘭人之書？ ── 的『必殺之技』或『必贏之論』。假使一個人對『機會之信念』不符合『機率公理』，那他將不免於被算計『預定』 booked ，以至於會『必輸無疑』。作者不知為什麼要叫做『荷蘭人之書』，看到網路上有人探討此事『History of the Term Dutch Book』，有興趣的讀者可以參考看看。這裡列出一個典型的『賭注登記者』之『書』︰
| 賭馬號 | 提供賠率 | 實際機率 | 賭金 | 勝金 |
|---|---|---|---|---|
| 1 | 公平對賭 | 1/2 = 0.5 | $100 | $100+$100=$200 |
| 2 | 3 : 1 對賭 | 1/4 = 0.25 | $50 | $50+3x$50=$200 |
| 3 | 4 : 1 對賭 | 1/5 = 0.2 | $40 | $40+4x$40=$200 |
| 4 | 9 : 1 對賭 | 1/10 = 0.1 | $20 | $20+9x$20=$200 |
| 總計︰1.05 | 總計︰$210 | 總是︰$200 |
那麼這個『賭博』是『公平』的嗎？我們應該如何思考『公平』的呢？如果說擲一個骰子，得到六點叫『贏』，其它點數就『輸』，如此按造機率法則，六次賭局中，平均一次能『贏』，五次會『輸』，要是兩人同意這樣是『公平』的『賭博』，『賭注』總金額 
的『分配』，將會是『機會小』的出 
和『機會大』的出 
，然後『贏者全拿』的吧！這種玩法的『公平性』在於大數法則下計算的輸贏『期望值』 兩方『相等』，都是 。假使是在『丟硬幣』賭『正反面』時，來看這種『分配方式』，各家出 
，或許會更『直覺』上認為是『公平』的吧。這也就是講，一個『公平的賭局』，『贏率』加上『輸率』的總和是『一』，在大數法則下之『輸贏』的『期望值』應當『相等』。如是前述那個『賭注登記者』之『書』要是『全押』得花 ＄210，最終『只得』 ＄200，用『大數法則』推究，又怎麽能是合理的呢？？雖有『賭性堅強』的人可能會議論說︰即使是用『9︰1 對賭』，我一定也『是個贏家』！！也許也只能說他『誤解』了所謂的『公平性』的啊！長時間來講，那就是吸血的『金錢幫浦』，這也就是『經濟學』所說的『常串等值貿易』，竟然有一方『老是得益』，另一方卻『總會失利』，真難到該有此理的嗎？？
我們之前曾用『條件機率』談論『睡美人的問題』的『機率大小』之『爭論』。這個『條件機率』在歷史上最早是因英國數學家托馬斯‧貝氏 Thomas Bayes 所提出的一種對『機率的解釋』，它將『機率定義』為︰一人對某個命題之『相信度』。或許及於那個『相信度』如何因為『新的資訊』之『增減』而變化。『貝氏』的這個『主觀機率論』後來逐漸成為『非主流』的想法，所謂之『客觀機率』事件『發生頻率』的支持者佔了上風。也許二十世紀初，『量子力學』的『機率問題』的推波助瀾，更加深了所謂的『事件』之『觀察者』是『主觀』的或者是『客觀』的，之天下『大哉辯』！因而『機率』到底是『什麼』？就會是人們不得不『思考』與『面對』之問題的了！！
義大利機率論者 Bruno de Finetti 所認為︰
You must set the price of a promise to pay ＄1 if John Smith wins tomorrow’s election, and $0 otherwise. You know that your opponent will be able to choose either to buy such a promise from you at the price you have set, or require you to buy such a promise from him/her, still at the same price. In other words: you set the odds, but your opponent decides which side of the bet will be yours. The price you set is the “operational subjective probability” that you assign to the proposition on which you are betting.
持續迴盪於時空中！！