物理哲學·下中………

有些長期從事科學的教育者，發現數理學習的困難度，可以排列成『邏輯』<『數學』<『機率』這樣的次序。這可讓人覺得十分有意思，難道是說『必然的』<『抽象的』<『不確定』？或許人們不能輕易覺察之『無意識』的『參照點』就是對事物觀點『兩極化』的由來。就好像在《改不改？？變不變！！》一文中所談到的一些『悖論』彷彿是『腦筋急轉彎』的一般！

唐吉訶德‧大戰風車

西班牙作家塞萬提斯名著
《唐吉訶德》開場白︰

En un lugar de la Mancha, de cuyo nombre no quiero acordarme, no ha mucho tiempo que vivía un hidalgo de los de lanza en astillero, adarga antigua, rocín flaco y galgo corredor.

曼查有個地方，地名就不用提了，不久前住著一位貴族。他那樣的貴族，矛架上有一支長矛，還有一面皮盾、一匹瘦馬和一隻獵兔狗。

《唐吉訶德》裡有一段，說︰

桑丘‧潘薩在他治理的島上頒布一條法例，規定過橋的旅客必需誠實地表示自己的目的，否則就要接受絞刑。有一個旅客在見到橋上的告示後，宣稱自己過橋是要接受絞刑的。

這使執法者感到為難：如果旅客的言論為真，則他應被釋放並不得受絞刑，但如此一來旅客言論即變為假。如其言論為假，則他會被絞死，但如此一來其言論即變為真。該旅客被帶到桑丘面前，而桑丘最後把他釋放。

一六零五年始，塞萬提斯寫了一本『反騎士』的小說，他怎知四百年後，美國的百老匯將其『唐吉訶德』變裝成了『逐夢者』。『正港』是有著『阿 Q 精神』的『夢幻騎士』，勇往直前『非理性』的『挑戰』當代社會中的一切『不合理性』現象，絕不退縮。宛如許多的『悖論』常起源於『自我指涉』之『誤謬』，為什麼呢？

『人的行為』並不外於他的『整體行為』，『人之言思』也屬於他的『全部言思』。於是乎，在『日久天長』中，難到不可能發生，有『一鬼』以為︰它並非『已死之人』，又有『一人』認為︰他就是『活著的鬼』。如果說︰昨日之我，譬如今日死；那麼今日之我，就將明日亡。如是議論，人麽真的能理解『時間』是什麼？『光陰』之所以是『公平』的，或許祇在於『如何使用』操之在人的吧！就像一個『推動』社會的『改革者』，期盼能免於︰先生，他們敗壞了所有價值，我們打垮了他們，不過我們也不知道如何重建那些他們曾經打垮之價值的哩！！

德國數學家約翰‧彼得‧古斯塔夫‧勒熱納‧狄利克雷 Johann Peter Gustav Lejeune Dirichlet 給出了現今我們叫做『函數』 function 的『正式定義』。狄利克雷講了一個『很直覺』的『鴿巢原理』︰

假使有 $n$ 個『籠子』和 $n+1$ 隻『鴿子』，如果所有的 $n+1$ 隻『鴿子』都被關在 $n$ 個『籠子』裡，那麼至少有一個『籠子』中有 $2$ 隻『鴿子』。

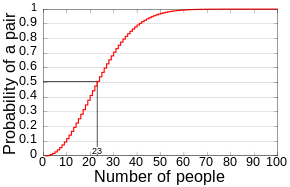
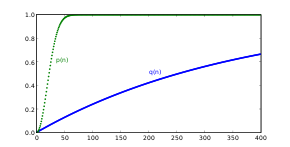
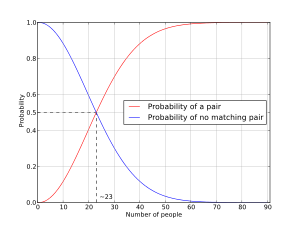
只不過在『某一情境』裡『直覺知道』的概念，『換一狀況』卻未必是『是曾相識』。舉個例說，有一位『公主』認為︰頭髮就是煩惱絲，於是決定只嫁給『頭髮一樣多』的人，這可讓曾以『公主』頭髮『又多又美』為榮的父王母后煩惱不已。那麼這個『公主』能夠嫁得出去嗎？這個『王國』能有未來之『繼承人』嗎？？此國雖然不大，卻也是有數千萬人，不知是『重賞之下必有勇夫』或是講『禮賢下士總有能人』，於是有人宣稱『他有辦法』解此『危難』。就在『國王』賞他之後，他說了『所謂辦法』，使得『國王』大樂，之後那個『公主』之『母后』更樂，更是『賞賜有加』。於是天下議論紛紛有『這種辦法』的嗎？？據後來『可靠消息』說，那人不過是說了︰『人類的頭髮根數』不可能『超過百萬』根，一個有『數千萬人』之國又怎麽可能會『沒有匹配』的呢？？作者不知果然的耶！『髮生髮落』彷彿就一定是『其數隨機』；難到果真『不可能』設想『髮數絕不相同』之國的勒！此後一直有人問著『公主歸宿』到底卻是如何？傳聞說她嫁給了『頭髮一樣多』之『心上人』的了！也許更不必說有幾多人，結果他們的『生日』可能『相同』或者『不同』的了！！