驢橋定理

驢橋定理（拉丁語：Pons asinorum），也稱為等腰三角形定理，是在歐幾里得幾何中的一個數學定理，是指等腰三角形二腰對應的二底角相等。等腰三角形定理也是歐幾里得的幾何原本第一卷命題五的內容。

有關其名稱驢橋定理的由來有二種：一種是幾何原本中的示意圖即為一座橋，另外一種比較廣為大家接受，是指這是幾何原本中第一個對於讀者智力的測試，並且做為往後續更困難命題的橋樑^[1]。幾何學是列在中世紀的四術之中，驢橋定理是在幾何原本的前面出現的較困難命題，是數學能力的一個門檻，也稱之為「笨蛋的難關」^[2]，無法理解此一命題的人可能也無法處理後面更難的命題。

無論其名稱的由來為何，驢橋定理一詞也變成是一種隱喻，是指對能力或了解程度的關鍵測試，可以將了解及不了解的人區分開來^[3]。

Pons asinorum

In geometry, the statement that the angles opposite the equal sides of an isosceles triangle are themselves equal is known as the pons asinorum (Latin pronunciation: [ˈpons asiˈnoːrʊm]; English /ˈpɒnz ˌæsᵻˈnɔərəm/ PONZ-ass-i-NOR-(r)əm), Latin for “bridge of donkeys”. This statement is Proposition 5 of Book 1 in Euclid‘s Elements, and is also known as the isosceles triangle theorem. Its converse is also true: if two angles of a triangle are equal, then the sides opposite them are also equal.

The name of this statement is also used metaphorically for a problem or challenge which will separate the sure of mind from the simple, the fleet thinker from the slow, the determined from the dallier; to represent a critical test of ability or understanding.^[1]‘

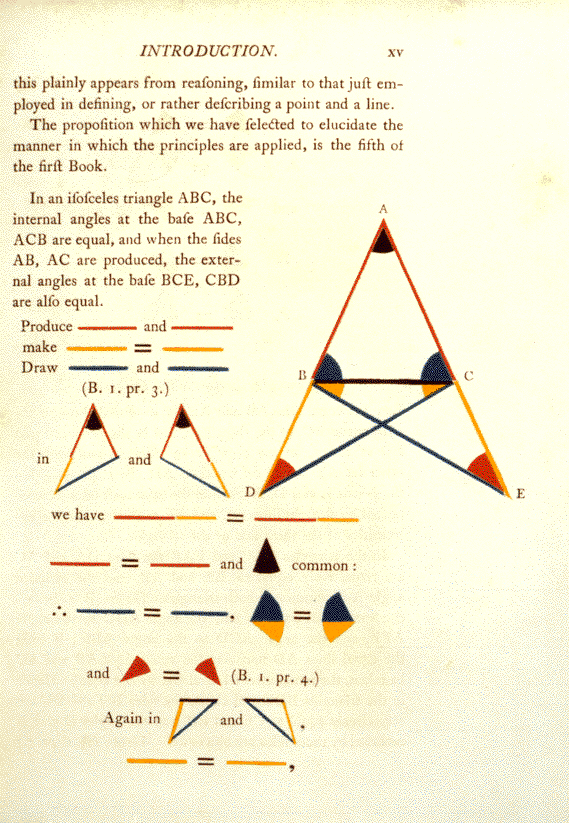
byrne_preface-15

Byrne版幾何原本中，驢橋定理的內容，有列出部份歐幾里得的證明

假如兩個三角形全等之第一原理為 SAS ── 夾角相等、夾角之兩邊亦皆對等 ── ，那麼作等長之延伸線段，迭代使用 SAS 證明，的確需要一番思慮。若是 SSS ── 三邊長都對應相等 ── 當第一原理，或許只需在等腰三角形之底取中點，就可藉 SSS 得出兩底角相等。據知幾何原本裡根本沒有 SSS 全等，這又為什麼呢？難到是因為它不夠直覺嗎？還是以一邊為底，兩端點各依所餘兩邊作圓，此二圓將相交於兩點，那要如何判定所形成的這兩個三角形全等的呢？？也許 SSS 之證明可以藉著在頂點處作條平行於底邊的平行線︰

『歐幾里得』的『平行公設』 ── 經過『線外』一『點』，只能作一條『平行線』平行該『線』 ──，或許正因為不夠『直覺』，然而又有人將它看成了『公理』，於是乎長期以來議論不斷，如此經過了兩千多年。一八二零年時，俄國數學家『尼古拉‧伊萬諾維奇‧羅巴切夫斯基』 Никола́й Ива́нович Лобаче́вский 想用『歸謬法』證明︰假使僅『反對』了『平行公設』 ── 假設有兩條平行線 ── ，但是卻『保留』著『其它公設』，這樣的『幾何系統』是不是會發生內部之『邏輯矛盾』的呢？本來是想『證明』平行公設的『必要性』，結果意外『成立』了一門『新的幾何學』，這就是第一個被提出的『非歐幾何學』。如果從『羅氏幾何學』建構方法來看，我們可以『知道』只要『選擇』邏輯上不矛盾的『一些公理』都有可能『成立』一種『幾何學』。這樣我們的『大自然』它會『選擇』特定的『幾何學』的嗎？假使果真有這個『幾何學』，我們又要『依據』什麼才能『判斷』它是『真實』的呢？？因此我們或許更當細思『先驗知識』與『後驗知識』之間的大哉『辯』與『辨』的吧！！

三種平行假設

笛沙格定理

如果A.a，B.b，C.c 共點，那麼 (A.B)∩(a.b)，(A.C)∩(a.c)，(B.C)∩(b.c) 共線。

雙曲面幾何學
多條平行線

球面幾何學
沒有平行線

─── 摘自《【Sonic π】電聲學之電路學《四》之《 !!!! 》上》

在此頂點兩端都可取一點，依據 SAS 及內錯角相等，全等於 SSS 之三角形。如是再因平行線的唯一性而得證。傳聞愛因斯坦小時並不了了，嘗如倔驢般畫了幾百個直角三角形，只求能實證畢氏定理，豈非反倒助其後發先至的呢！！因是一時之會與不會從來不是問題，想不想會才是大哉問的哩？？！！

雖然通常求解一般性問題︰ $a^2 + b^2 = c^2$ 的所有整數解。

勾股數組

勾股數組是滿足勾股定理 $a^2 + b^2 = c^2$ 的正整數組 $(a,b,c)$ ，其中的 $a,b,c$ 稱為勾股數。例如 $(3,4,5)$ 就是一組勾股數組。

任意一組勾股數 $(a,b,c)$ 可以表示為如下形式： $a=k(m^2-n^2), b=2kmn, c=k(m^2+n^2)$ ，其中 $k, m,n\in \mathbb{N*},m>n$ 。

phzscn

趙爽勾股圓方圖證明勾股定理法動畫

要比特定問題︰ $x^2 + y^2 = {17}^2$ 的整數解。

困難的多。事實上這並非是必然的矣！！？？

就讓我們以一般光學矩陣為例

$\left( \begin{array}{cc} A & B \\ C & D \end{array} \right)$

探討前後焦距、主平面、以及成像法則吧。如是也可知道 ABCD 這四個符號，實有著深刻的意蘊，故能決定那光學系統之行為。

【前後焦距】

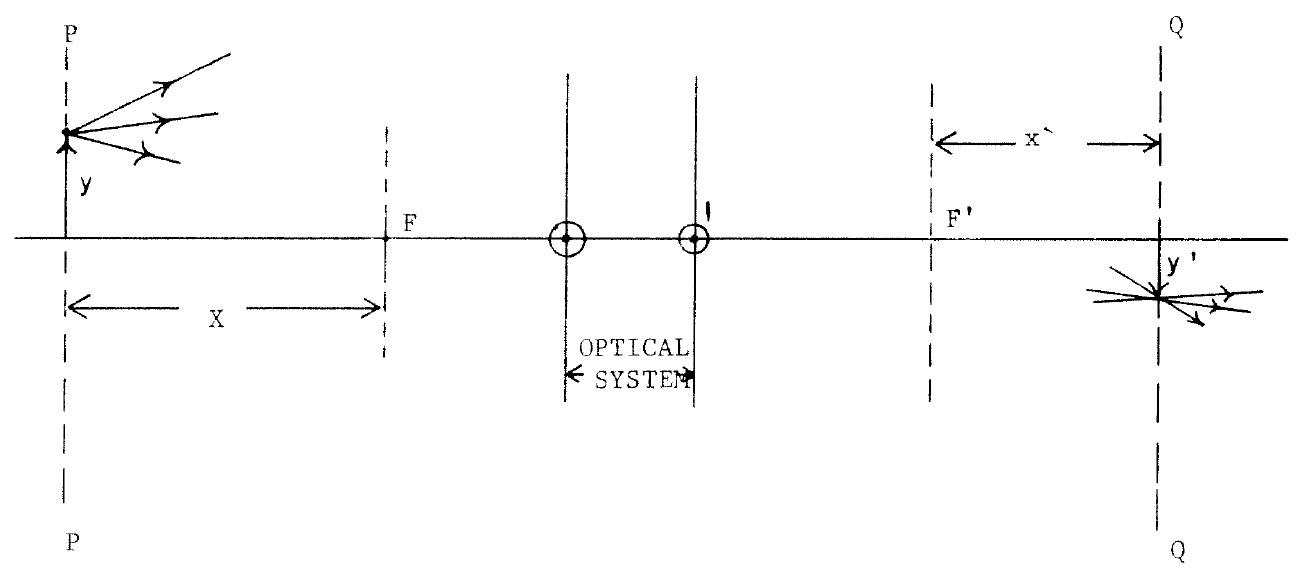
牛頓成像公式

依慣例假設光的行徑方向是左→右，遇一光學系統，此處發生折射【※ 或反射】，這處稱之為『前端點』 $V$ ，而後行經此光學系統，最終發生折射處【※ 或反射】稱之為『後端點』 $V'$ 。這構成了『端點面參考系』，也就是『前後焦距』以平行光『度量』聚散的座標系。簡單推導如下︰

pi@raspberrypi:~ -\frac{A}{C}-\frac{D}{C}\frac{1 - A}{C}\frac{1 - D}{C} det  \left( \begin{array}{cc}

A &  B  \\

C & D \end{array}  \right)  = A D - B C = 1f_{eff}= -\frac{A}{C} - \frac{1 - A}{C} = - \frac{1}{C}f_{eff}= -\frac{D}{C} - \frac{1 - D}{C} = - \frac{1}{C}\frac{1}{do} + \frac{1}{di} = \frac{1}{f_{eff}}$
果能有疑義焉☆

日	一	二	三	四	五	六
« 4 月
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31

FreeSandal

光的世界︰【□○閱讀】樹莓派近攝鏡‧下‧答之承

驢橋定理

Pons asinorum

勾股數組

輕。鬆。學。部落客