樹莓派、樹莓派之學習、樹莓派之教育

λ 運算︰概念導引之《補充》※真假祇是個選擇？？

200px-Cathédrale_d'Auch_20

約櫃

約櫃施恩座

義大利羅馬真理之口

《聖經》出埃及記25:10-22

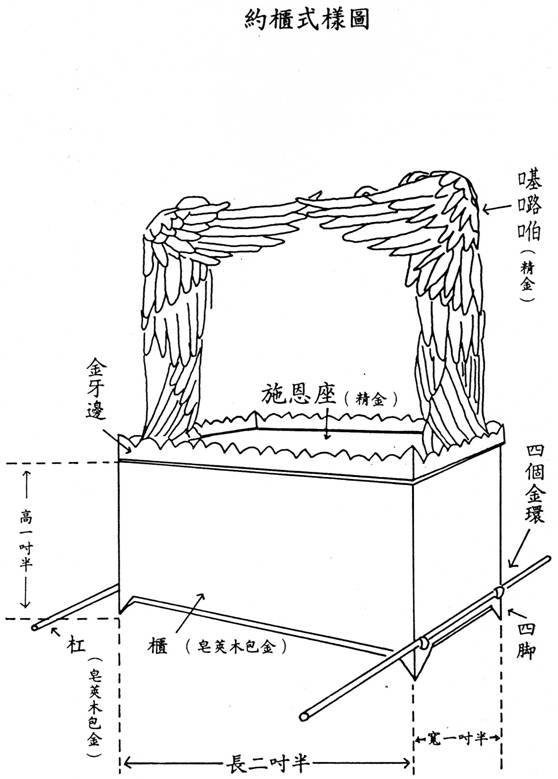
約櫃
10 “他們要用皂莢木做一個櫃，長一百一十公分，寬六十六公分，高六十六公分。 11 你要用純金包櫃，內外都要包上；櫃上的四圍要做金邊。 12 你要鑄造四個金環，安放在櫃的四腳上，兩個環在這邊，兩個環在那邊。 13 你要用皂莢木做幾根櫃槓，並要用金包裹起來。 14 你要把櫃槓穿在櫃旁的環中，以便用槓抬櫃。 15 櫃槓要常留在櫃的環中，不可抽出環外。 16 你要把我賜給你的法版放在櫃裡。 17 你要用純金做施恩座，長一百一十公分，寬六十六公分。 18 你要用黃金錘成兩個基路伯，放在施恩座的兩端。 19 這端做個基路伯，那端做個基路伯，二基路伯要與施恩座連在一起製造，在施恩座的兩端。 20 二基路伯要在上面展開雙翼，遮掩施恩座，基路伯的臉要彼此相對，他們的臉要朝著施恩座。 21 你要把施恩座安放在櫃頂，又要把我賜給你的法版放在櫃裡。 22 我要在那裡和你相會，也要從施恩座上面，從二基路伯之間，告訴你一切我命令你傳給以色列人的事。

作者不知義大利羅馬的『真理之口』將會如何來決定『何謂是真？』而『什麼又是假』的呢？？

又為什麼『真』與『假』的 λ表達式是

TRUE =_{df} (\lambda x. ( \lambda y. x))
FALSE =_{df} (\lambda x .( \lambda y. y))

的呢？如果我們將『運算』看成『黑箱』，用『實驗』的方法來『研究』輸入輸出的『關係』，這一組有兩個輸入端的黑箱，對於任意的輸入『二元組』pair  (u, v)，有︰

(((\lambda x. ( \lambda y. x)) u) v) = u
(((\lambda x. ( \lambda y. y)) u) v) = v

，於是將結論歸結成︰貼『真』標籤的箱子的『作用』是『選擇』輸入的『第一項』將之輸出；而貼『假』標籤的箱子的『作用』是『選擇』輸入的『第二項』將之輸出。

假使一位『軟體』工程師在函式『除錯』時，可能會採取在那個『函式』內『輸出』看看得到的『輸入』參數值是否正確？

於是將結論歸結成︰『真』標識符的函式『作用』是『選擇』輸入參數的『第一項』；『假』標識符的函式『作用』是『選擇』輸入參數的『第二項』。

那麼對一個已經打開的『白箱』，又知道作用的『函式』，怎麼會概念上『一頭霧水』的呢？？如果細思一個邱奇自然數『 0 』， 0 =_{df} (\lambda f. ( \lambda x. x))，這跟『假』的 λ表達式有什麼不一樣的呢？那難道我們能說『0』就是『假』的嗎？在《布林代數》中的『0』與『1』其實是未定義的『兩態』基元概念── 就像歐式幾何學裡的『點』、『線』和『面』是『基本』概念一樣 ──，因此不管說它是『電壓高低』或者講它是『電流有無』的『數位設計』可以應用布林代數。要是我們將『0』『1』與『假』『真』概念連繫起來看，『布林邏輯』就是『真假』是什麼的『系統化』之概念內涵開展，它的『整體內容』呈現『兩態邏輯』的『方方面面』，縱使至於『孤虛』NAND 一個邏輯概念就足夠了，對於『 0 與 1 』概念本身還是『三緘其口』。

其實『 λ表達式』建構上表徵『函式』── 假使代表某種『概念』──的『子函式組織』以及『子函式應用』之『結構』。而這個所謂的『結構』只是在『 λ語言』的『語法』上『呈現』的，所以想要如何『語意詮釋』呢？也許天下《一指》可知，萬物《一馬》可比的吧！！

LC選項設定

LC字典初始內容

現在就讓我們用 Lambda Calculator 探究一下 λ 運算的『真假邏輯』化約。首先將『選項』設定如下︰

一、選擇『正規求值』Normal Evaluation
二、選擇『帶數目的純 λ 運算』Pure Calculus With Numerals
三、不選『使用 \eta 變換』Use Eta Reductions
參見左上圖。

為什麼不使用 \eta 變換的呢？比方考慮下面的函式化約

(\lambda p. ( \lambda x. ( \lambda y. ((p x) y))))
\equiv_{\eta} (\lambda p. ( \lambda x. (p x)))
\equiv_{\eta} (\lambda p. p)

，這並不是我們對這個『三元』p, x., y 函式的概念想法，它表達的是『有一個變元 p，應用於變元 x 後，將它的結果 (p x) 再次應用於變元 y 之上 ((p x) y)』。然而由於 ( \lambda y. ((p x) y)) 中的 (p x) 表達式裡並沒有 y 變元，所以就被『 \eta 變換』的了，再次經過『 \eta 變換』後，最終變成了 (\lambda p. p) 的『恆等函式』了，這也是為什麼『 \eta 變換』會有爭議的原由之一。由於 Lambda Calculator 軟體支持一般『去除減少括號』以便於『書寫』與『閱讀』的『左向優先結合』和『最大函式跨距』之『函式應用約定』，因此上式就可以改寫成︰

\lambda p. \lambda x. \lambda y. p \ x \ y

，當你輸入帶有括號的『 λ表達式』它會將之『去除掉不必要』的括號『簡化』，可以見之於上圖的『字典』Show Text 的內容︰

FALSE [(\x.(\y.y))] = \x.\y.y
IFTHENELSE [(\p. ( \x. ( \y. ((p x) y))))] = \p.\x.\y.p x y
ISZERO [(\n. ((n (\x.FALSE)) TRUE))] = \n.n (\x.FALSE) TRUE
TRUE [(\x.(\y.x))] = \x.\y.x

，它的『格式』是《『標識符』【定義輸入】=『簡化』》。

ISZERO-0
圖一

ISZERO-1
圖二

ISZERO-0
圖三

ISZERO-1
圖四

IFTHENELSE-TRUE
圖五

IFTHENELSE-FALSE
圖六

IFTHENELSE-ISZERO
圖七

現在讓我們先將上述的定義輸入字典。其中『是零嗎』ISZERO 是一個『是或不是』的邏輯判斷，一般稱作『謂語』或叫『述詞』Predicate ︰

\lambda n. n (\lambda x. FALSE) TRUE

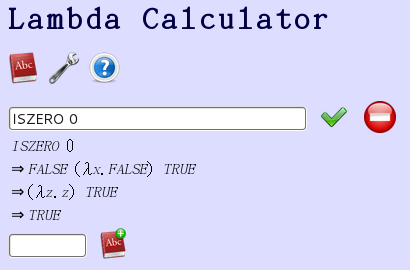
，左圖一是邱奇自然數 0 的推導︰ISZERO \ (\lambda f. (\lambda x. x))
1\equiv_{\beta} ISZERO \ FALSE
2\equiv_{\beta} FALSE \ (\lambda x. \ FALSE) \ TRUE
3\equiv_{\beta} (\lambda y. \ y) \ TRUE
4\equiv_{\beta} TRUE

由於『 0 』和『假』的結構相同，所以『第一步』中它被替換成了『FALSE』。『第二步』展開『ISZERO』的標識符，將變元 n 賦與了『FALSE 0』的值。『第三步』展開(FALSE (\lambda x. FALSE) )，最左邊的 FALSE 之變元 x 被賦與 \lambda x. FALSE 的值然後將之拋棄，最後只剩下了 \lambda y. y。最後『第四步』變元 y 得到了『真』。

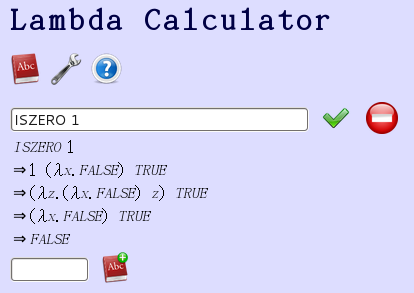
左圖二是邱奇自然數 1 的推導，如果用 Lambda Calculator  選擇『純 λ 運算』的選項，顯示為︰

ISZERO (λf.λx.f x)
⇒ (λf.λx.f x) (λx.FALSE) TRUE
⇒ (λx.(λi0.FALSE) x) TRUE
⇒ (λx.FALSE) TRUE
⇒ FALSE

左圖三和左圖四是用 Lambda Calculator 中定義的『自然數』來作相同的推導，讀者可以自行參考。

當然『IFTHENELSE』就是程式語言中的︰

如果 p 為真，執行 x，否則就執行 y

，左圖中的五、六、七是它使用的例子。

那我們能從它的『定義』
IFTHENELSE =_{df} \lambda p. \lambda x. \lambda y. p \ x \ y
看出是『這個意義』的嗎？

因此才說 λ 運算的『函式』是由『抽象』得來，λ 表達所建構的『結構』也是『抽象』的，所以不同的『概念系統』彼此『抽象化』後的『結構』可以『相同』。

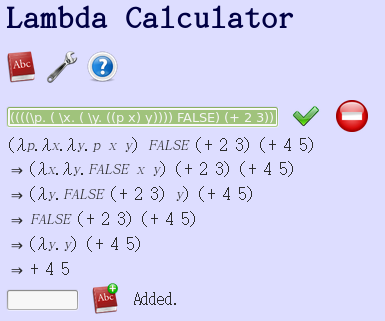
如果從程式語言的『使用觀點』考慮上圖七的

IFTHENELSE (ISZERO 0) (+ 2 3) (+ 4 5)

，如果我們知道『IFTHENELSE』的『語法』定義與『功能』，那麼一個『合語法』的『表達陳述』自然得到它所定義的運算結果『(+ 2 3)』，至於運算的『化約過程』在『語用』的角度上看成了『黑箱』，通常只有在『結果』不如『預期』時，或許你自己就是那『語言』的『創始者』，才會觀察『運算過程』，試圖發現各個『定義』所構成之『系統』內部的『相容性』和『一致性』之問題的吧！！

就讓我們用 Lambda Calculator 之『純 λ 運算』，寫個『孤虛』NAND 邏輯，推算到底『牛郎織女』是『相會的成』還是『相會不成』的呢？？

下面是『孤虛語』的『字典定義』︰

且 [\p. \q. p q 假] = \p.\q.p q 假
假 [\x. \y. y] = \x.\y.y
孤虛 [\u. \v. 非 ( 且 u v )] = \u.\v.u v 假 假 真
或 [\p. \q. p 真 q] = \p.\q.p 真 q
有數 [\f. \x. (f x)] = \f.\x.f x
沒嗎？ [\n. n (\x. 假) 真] = \n.n (\x.假) 真
真 [\x. \y. x] = \x.\y.x
若則否則 [\p. \x. \y. p x y] = \p.\x.\y.p x y
非 [\p. p 假 真] = \p.p 假 真

已知『且 (孤虛 假 假) (孤虛 真 真) 』為『假』，那麼

『 若則否則  (且 (孤虛 假 (非 假) ) (孤虛 真 (非 真) ))  (沒嗎？ 假) (沒嗎？ 有數) 』是『成』還是『不成』的呢？？

金剛石

人造金剛石

《金剛經》

佛告須菩提，凡所有相，皆是虛妄，若見諸相非相，則見如來。

 

也許『不變的愛』 ( λ 之. (不變的愛  之)) 只能是一個『行為的純函式』，她不製造任何的『副作用』。對於『之人』『之物』的『初衷』不變，次次回回保有『愛之初心』，不會生此一時，彼一地的『妄念』，或可至之於『終身』，方可許諾能『永恆』！！