最小上界性質

Let S be a non-empty set of real numbers:
A real number x is called an upper bound for S if x ≥ s for all s ∈ S. A real number x is the least upper bound (or supremum) for S if x is an upper bound for S and x ≤ y for every upper bound y of S.

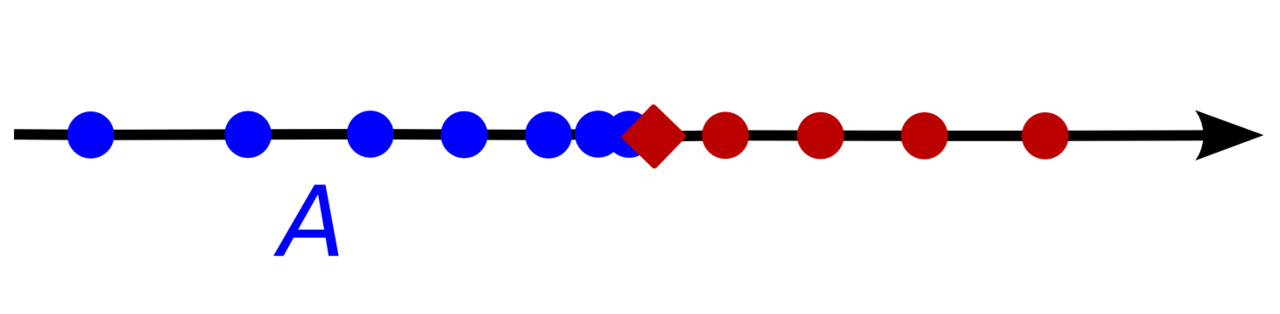
從『疊套區間』的觀點來看，一個『超實數』 $r^{*} = r + \delta x$ 就可以表達成 $[r - \delta \epsilon, r + \delta \epsilon]$ ，而且說 $st \left( [r - \delta \epsilon, r + \delta \epsilon] \right) = \{r\}$ ，由於它只有『唯一的』一個元素，所以被稱作『單子集合』 singleton set。假使我們思考一個『單調上升有上界』 $a_n, a_{n+1} > a_n, a_n < U, n=1 \cdots n$ 的『序列』，會發現它一定有『最小上界』。假設 $H$ 是一個『巨量』，那麼 $st \left( \bigcap \limits_{1}^{\infty} [a_n, 2 a_H -a_n] = a_{\infty} \right)$

。這就是『實數』的『基本性質』，任何一有極限的『序列』收斂於一個『唯一』的『實數』，一般稱之為『實數』的『完備性』 completeness，由於我們是站在『超實數』的立場，選擇了『疊套區間』的觀點，加之以『無窮小』量不滿足『實數』的『阿基米德性質』，所以這個『實數』的『完備性』只是從『疊套區間』確定了一個『單子集合』推導的結論。對比著來看，這一個『有理數』序列 $x_0 = 1, x_{n+1} = \frac{x_n + \frac{2}{x_n}}{2}$ 的『極限』 $x_{\infty} = \sqrt{2}$ ，它可從求解 $x_H = \frac{x_H + \frac{2}{x_H}}{2}$ 得到，然而它並不是『有理數』，所以說『有理數』不具有『完備性』。那麼對一個『非空有上界』的『集合』 $S$ ，也可以用『二分逼近法』論證如下︰

由於 $S$ 有上界，就說是 $b_1$ 吧，因為 $S$ 不是空集合，一定有一個元素 $a_1$ 不是它的上界。這兩個序列可以遞迴的如此定義，計算 $\frac{a_n + b_n}{2}$ ，如果它是 $S$ 的上界，那麼 $a_{n+1} = a_n, \ b_{n+1} = \frac{a_n + b_n}{2}$ ，否則 $S$ 中必有一個元素 $s$ ，而且 $s > \frac{a_n + b_n}{2}$ ，此時選擇 $a_{n+1} = s, \ b_{n+1} = b_n$ ，如此 $a_1 \leq a_2 \leq a_3 \leq \cdots \leq b_3 \leq b_2 \leq b_1$ 而且 $a_H - b_H \approx 0$ ，所以一定存在一個 $L = a_{\infty} = b_{\infty}$ ，此為 $S$ 之最小上界。

同理 $S$ 的補集 $R - S$ 就會有『下界』，而且會有『最大下界』。因此我們將一個有『上界』與『下界』的集合，簡稱之為『有界集合』。

─── 《【SONIC Π】電路學之補充《四》無窮小算術‧下》

實數的『完備性』邏輯上蘊涵了『介值定理』︰

若問一個人從山腳走到山頂，是否他經過了此山的所有高度？可能有人會說題意模糊難於論斷。也可能有人依據常理常義衡量講當然如此。想那山道蜿蜒是『連續』的，人腳步伐落處卻是『離散』的，固然『連續』包含著『離散』！！然而『離散』能近似『連續』耶？？所謂天衣無縫，實數方才完備乎！！

Completeness of the real numbers

Intuitively, completeness implies that there are not any “gaps” (in Dedekind’s terminology) or “missing points” in the real number line. This contrasts with the rational numbers, whose corresponding number line has a “gap” at each irrational value. In the decimal number system, completeness is equivalent to the statement that any infinite string of decimal digits is actually a decimal representation for some real number.

Depending on the construction of the real numbers used, completeness may take the form of an axiom (the completeness axiom), or may be a theorem proven from the construction. There are many equivalent forms of completeness, the most prominent being Dedekind completeness and Cauchy completeness (completeness as a metric space).

因其完備，對『連續函數』而言，介值定理不得不然嗎！！？？

Intermediate value theorem

In mathematical analysis, the intermediate value theorem states that if a continuous function, f, with an interval, [a, b], as its domain, takes values f(a) and f(b) at each end of the interval, then it also takes any value between f(a) and f(b) at some point within the interval.

This has two important corollaries: 1) If a continuous function has values of opposite sign inside an interval, then it has a root in that interval (Bolzano’s theorem).^[1] 2) The image of a continuous function over an interval is itself an interval.

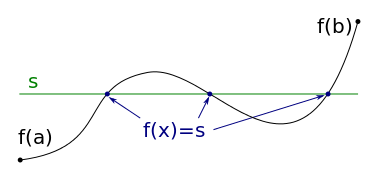
Intermediate value theorem: Let f be a defined continuous function on [a, b] and let s be a number with f(a) < s < f(b). Then there exists at least one x with f(x) = s

─── 摘自《時間序列︰生成函數‧漸近展開︰無限大等級 V》

然於如何『求根』乙事？卻是三緘其口哩！更別說當一個『多項式方程式』的『次方數』超過了『四階』就沒有『一般解』！！只得用數值方法耶？？

求根演算法

在數學和電腦運算中，對於一個已知的從實數集合對映到實數集合，或者從複數集合對映到複數集合的連續函數 $\displaystyle f(x)$ ，搜尋變數 $\displaystyle x$ 使得 $\displaystyle f(x)=0$ （此時，變數 $\displaystyle x$ $x$ 稱為 $\displaystyle f(x)=0$ 的根、 $\displaystyle f(x)$ 的零點）的演算法，稱為求根演算法。在許多情況下，函數的零點無法被準確計算出，也無法被解析解表示；是故，求根演算法在實數集合下只提供一個以浮點數表示的近似解，或者一個足夠小的解的存在區間，在複數集合下只提供一個複根的圓盤（輸出一個區間或一個圓盤等價於輸出一個根的近似值及其誤差上限）。

解方程式 $\displaystyle f(x)=g(x)$ 與求 $\displaystyle f(x)-g(x)$ 的根是等價的。因此求根演算法可以求解任何以連續函數定義的方程式。然而，許多情況下，求根演算法只能找到方程式的某些根，而不能保證所有根都能找到；特別指出，演算法未找到根，並不代表方程式確實無根。

大多數的數值求根演算法都使用疊代法，生成一個以方程式的根為極限的收斂數列。它們需要一個或多個根作為疊代的初期值，嗣後每次疊代都生成一個逐步逼近根的值。由於疊代法必須在有限步內終止於某個點，這些方法都只能提供一個根的近似值，而不能提供一個精確解。許多方法是通過代入上一個疊代值來計算一個輔助方程式，從而得出下一個疊代值的。此處所指的輔助方程式是指為了使源方程式的根是一個定點並使疊代值能更快地收斂到這些定點而設計的一個方程式，因此疊代值的極限是這個輔助方程式的一個定點。

求根演算法的效能是數值分析的研究範疇。一種演算法的效率可能大幅度取決於已知點的性質。例如，一部分演算法都使用輸入函數的導數（此要求函數不但連續，而且可導），而其他演算法則能用於任何一個連續函數。在一般情況下，數值演算法不能保證找到一個函數的所有根，因此演算法未能找到根並不能證明方程式無根。然而，對於多項式，存在特定的使用代數學性質以定位根的所在區間（或複根所在的圓盤）的演算法，這個區間（或圓盤）足夠小以能保證數值演算法（例如牛頓法）能收斂到唯一被定位的根。

考察其術︰

包圍法

包圍法是指通過疊代確定根的所在區間，並逐漸縮小其區間長度的演算法。當區間變得足夠小時，則認為根已經被找到。一般地，包圍法以介值定理為基礎，且能夠求出根的絕對誤差上限；而當函數是一個多項式時，還有其它基於施圖姆定理或笛卡兒符號法則的方法，能夠在一個區間內求出精確的根。

二分法

最簡單的求根演算法為二分法︰令 $\displaystyle f(x)$ 為一個連續函數，且已知存在區間 $\displaystyle [a,b]$ 滿足 $\displaystyle f(a)$ 符號互異。令 $\displaystyle c=(a+b)/2$ 區間的中點），則 $\displaystyle f(a)$ 和 $\displaystyle f(c)$ 或 $\displaystyle f(c)$ 和 $\displaystyle f(b)$ 中，必恰有一者符號互異，並將已知根所在區間的長度縮短為一半。對被縮短的區間重複上述步驟，直到找到根。

縱二分法具有強健性，但其只能求得區間內的一個且只有一位精度的解。此外在合適的條件下，亦存在其他能更快求得精確解的方法。

盈不足術法

盈不足術法與二分法相似。異處在於，盈不足術以方式計算出疊代點，

\displaystyle c={\frac {af(b)-bf(a)}{f(b)-f(a)}}.

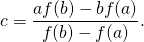
盈不足術法也類似於割線法。異處在於，盈不足術法不保留前兩次疊代點，而是在根的兩側各保留一點。盈不足術法能以較二分法更快的速度求根，且不會如割線法一樣發散（不收斂）；但在一些簡單實現的情形中可能因為捨入誤差而無法收斂。^{[需要解釋]}

Ridders法是盈不足術法的一個變形。其使用區間中點的函數值，構造出一個具有相同零點的函數，再用盈不足術法求解之。這個方法維持了一定的強健性外，亦使演算法更快收斂。

插值法

許多求根演算法通過插值來實現。即，使用上一步計算出的根的多個近似值，藉助一個以插值法求出的低次多項式，以逼近一個函數。然後計算多項式的根，並用其作新的函數的根的近似值，重複此流程。

兩個函數值可利用插值法求得一個一次多項式，即以一條直線逼近一個函數圖像。此乃割線法及盈不足術法的基礎。進而，三個函數值可求得一個二次函數，即以一條拋物線逼近一個函數圖像。此即Muller法。

疊代法

雖然所有求根演算法都通過疊代，但一個疊代的求根演算法，通常使用一種特定的疊代類型，包括定義一個輔助函數，應用上一步計算出的根的近似值，求得新的近似值。輔助函數到逹一個定點（到逹所需的精度），即新疊代的近似值充分接近上一個疊代值時，疊代停止。

牛頓法（及類似的以導數為基礎的方法）

牛頓法假定函數 $\displaystyle f$ 的導數是連續的。如果起始點距離根太遠，牛頓法可能不收斂。然而，其若收斂，速度將較二分法快，且通常為二次收斂。牛頓法也是一種重要的演算法，因為它能容易地推廣到高維問題。類似牛頓法且有更高次的收斂性的演算法為Householder法。具有三次收斂性的Householder法是Halley法。

割線法

將牛頓法中的導數替換為一個差分式，即得到割線法。這種方法的優點在於不需要計算導數，但其代價是收斂速度較慢（收斂次數約為1.6）。把割線法推廣到高維的演算法是Broyden法。

逆插值法

對函數 $\displaystyle f$ 進行逆插值，能夠避免插值法中出現複數。這種方法稱為逆二次插值法。其收斂速度漸近快於割線法；但當疊代離根較遠時，逆二次插值法往往表現不佳。

初始揣測『根之所在』，選址定基難有善法也★

比方講︰

『二分法』之所以強健，雖得『介值定理』之本，尚須先找到函數『變號區間』也；『牛頓法』

Newton’s method

In numerical analysis, Newton’s method, also known as the Newton–Raphson method, named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots (or zeroes) of a real-valued function. It is one example of a root-finding algorithm.

The Newton–Raphson method in one variable is implemented as follows:

The method starts with a function $f$ defined over the real numbers $x$ , the function’s derivative $f '$ , and an initial guess $x 0$ for a root of the function $f$ . If the function satisfies the assumptions made in the derivation of the formula and the initial guess is close, then a better approximation $x 1$ is

\displaystyle x_{1}=x_{0}-{\frac {f(x_{0})}{f'(x_{0})}}\,.

Geometrically, $(x 1, 0)$ is the intersection of the $x$ -axis and the tangent of the graph of $f$ at $(x 0, f (x 0))$ .

The process is repeated as

\displaystyle x_{n+1}=x_{n}-{\frac {f(x_{n})}{f'(x_{n})}}\,

until a sufficiently accurate value is reached.

縱使快速，有『解析幾何』的直覺，第一步踏錯怕會無『回頭路』矣。

猶恐讀者誤解所指，特以『單峰映象』例釋一下︰

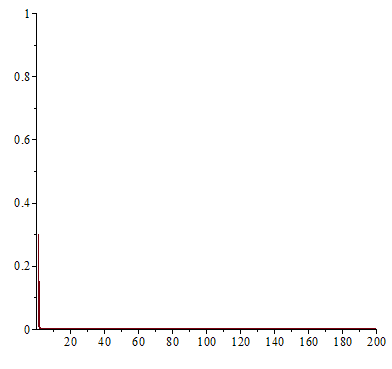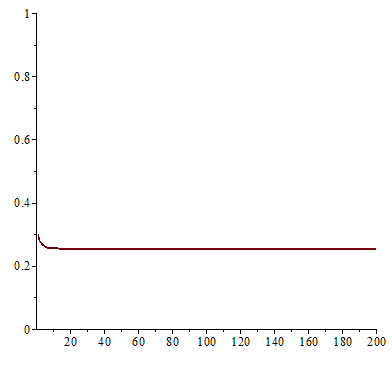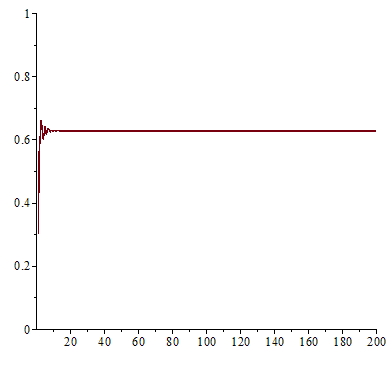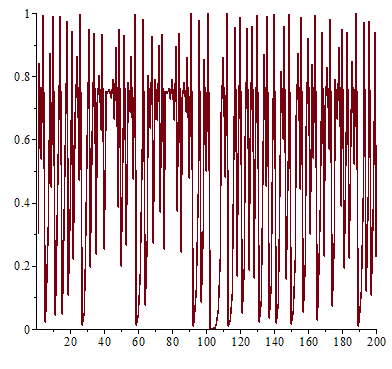
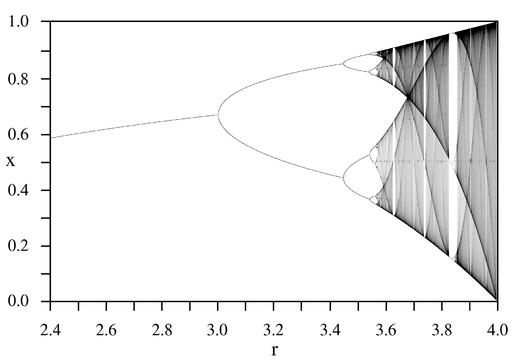
一九七六年，澳洲科學家 Robert McCredie May 發表了一篇《Simple mathematical models with very complicated dynamics》文章，提出了一個『單峰映象』 logistic map 遞迴關係式 $x_{n+1} = r x_n(1 - x_n), \ 0\leq x_n <1$ 。這個遞迴關係式很像是『差分版』的『 logistic equation』，竟然是產生『混沌現象』的經典範例。假使說一個『遞迴關係式』有『極限值』 $x_{\infty} = x_H$ 的話，此時 $x_H = r x_H(1-x_H)$ ，可以得到 $r{x_H}^2 = (r - 1) x_H$ ，於是 $x_H \approx 0$ 或者 $x_H \approx \frac{r - 1}{r}$ 。在 $r < 1$ 之時，『單峰映象』或快或慢的收斂到『零』；當 $1 < r < 2$ 之時，它很快的逼近 $\frac{r - 1}{r}$ ；於 $2 < r < 3$ 之時，線性的上下震盪趨近 $\frac{r - 1}{r}$ ；雖然 $r=3$ 也收斂到 $\frac{r - 1}{r}$ ，然而已經是很緩慢而且不是線性的了；當 $r > 1 + \sqrt{6} \approx 3.45$ 時，對幾乎各個『初始條件』而言，系統開始發生兩值『震盪現象』，而後變成四值、八值、十六值…等等的『持續震盪』；最終於大約 $r = 3.5699$ 時，這個震盪現象消失了，系統就步入了所謂的『混沌狀態』的了！！

………

回想之前『λ 運算』裡的『遞迴函式』，與數學中的『定點』定義，『單峰映象』可以看成函數 $f(x) = r \cdot x(1 - x)$ 的『迭代求值』︰ $x_1 = f(x_0), x_2 = f(x_1), \cdots x_{k+1} = f(x_k) \cdots$ 。當 $f^{(p)} (x_f) = f \cdots (p -2) \times f \cdots f(x_f) = x_f$ ，這個 $x_f$ 就是『定點』，下圖中顯示出不同的 $r$ 值的求解現象，從有『定點』向『震盪』到『混沌』。