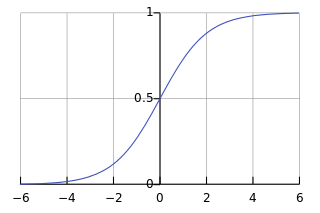
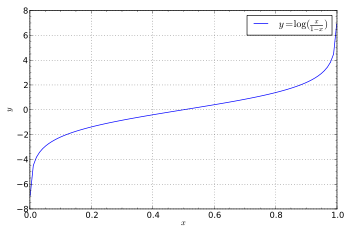
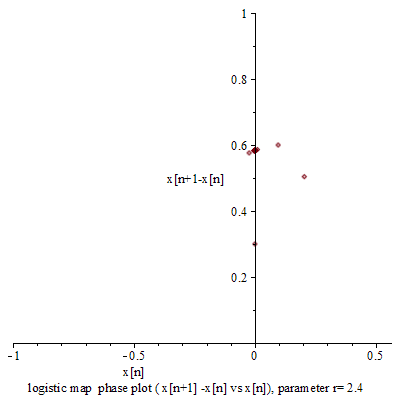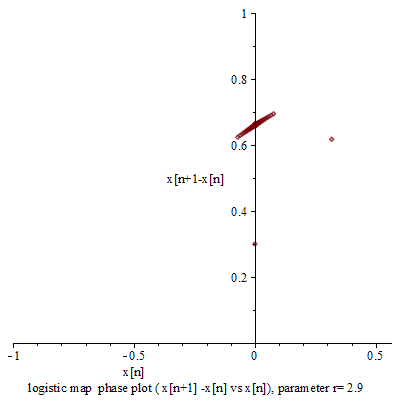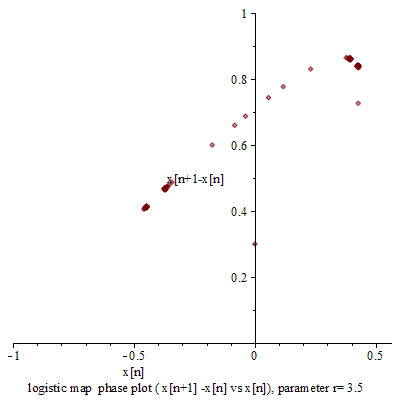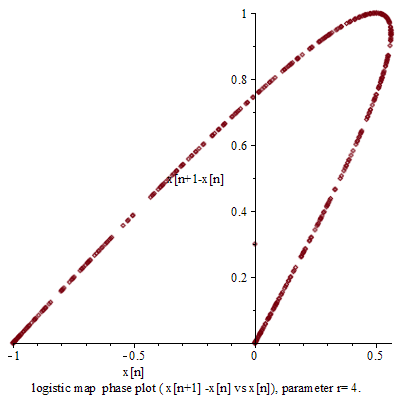一八三八年,比利時數學家 Pierre François Verhulst 發表了一個『人口成長』方程式,
![]()
,此處 ![]() 是某時的人口數,
是某時的人口數,![]() 是自然成長率,
是自然成長率, ![]() 是環境承載力。求解後得到
是環境承載力。求解後得到
![]()
,此處 ![]() 是初始條件。 Verhulst 將這個函數稱作『logistic function』,於是那個微分方程式也就叫做『 logistic equation』。假使用
是初始條件。 Verhulst 將這個函數稱作『logistic function』,於是那個微分方程式也就叫做『 logistic equation』。假使用 ![]() 改寫成
改寫成 ![]() ,將它『標準化』,取
,將它『標準化』,取 ![]() 與
與 ![]() ,從左圖的解答來看,
,從左圖的解答來看, ![]() ,也就是講人口數成長不可能超過環境承載力的啊!
,也就是講人口數成長不可能超過環境承載力的啊!
如果求 ![]() 的反函數,得到
的反函數,得到 ![]() ,這個反函數被稱之為『Logit』函數,定義為
,這個反函數被稱之為『Logit』函數,定義為
![]()
,一般常用於『二元選擇』,比方說『To Be or Not To Be』的『機率分佈』,也用於『迴歸分析』 Regression Analysis 來看看兩個『變量』在統計上是『相干』還是『無干』的ㄡ!假使試著用『無窮小』數來看 ![]() 和
和 ![]() ,或許更能體會『兩極性』的吧!!
,或許更能體會『兩極性』的吧!!
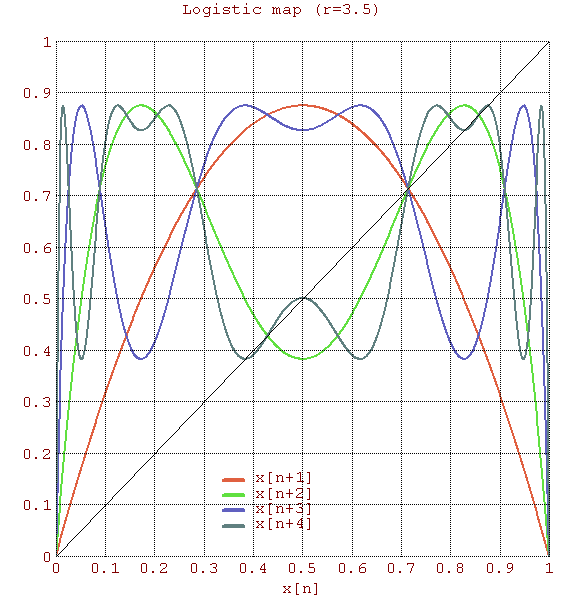
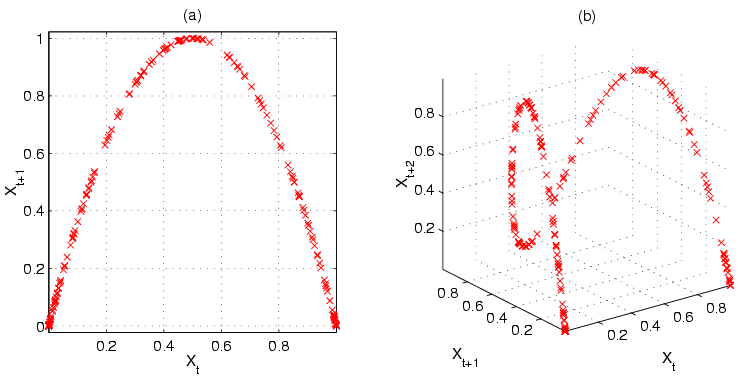
一九七六年,澳洲科學家 Robert McCredie May 發表了一篇《Simple mathematical models with very complicated dynamics》文章,提出了一個『單峰映象』 logistic map 遞迴關係式 ![]() 。這個遞迴關係式很像是『差分版』的『 logistic equation』,竟然是產生『混沌現象』的經典範例。假使說一個『遞迴關係式』有『極限值』
。這個遞迴關係式很像是『差分版』的『 logistic equation』,竟然是產生『混沌現象』的經典範例。假使說一個『遞迴關係式』有『極限值』![]() 的話,此時
的話,此時 ![]() ,可以得到
,可以得到 ![]() ,於是
,於是 ![]() 或者
或者 ![]() 。在
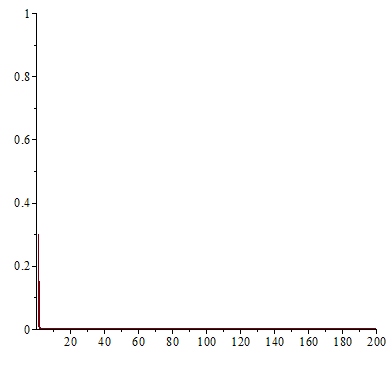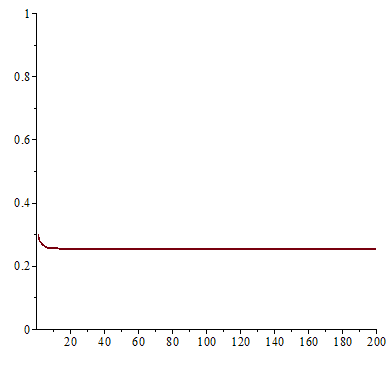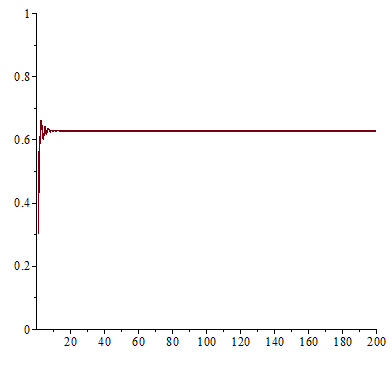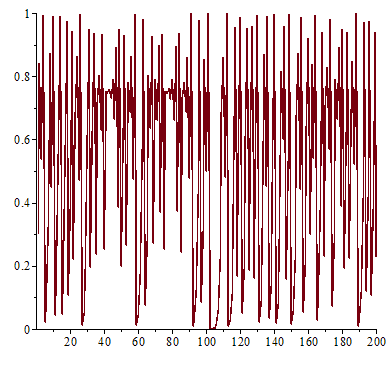
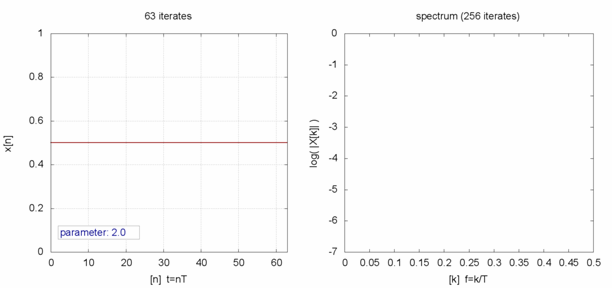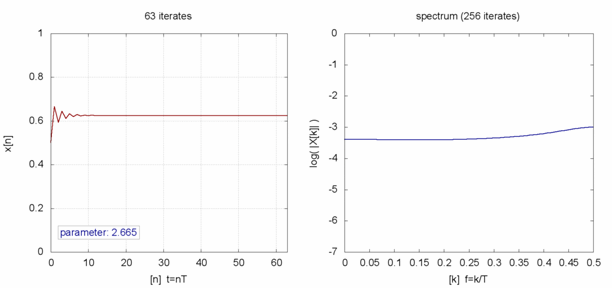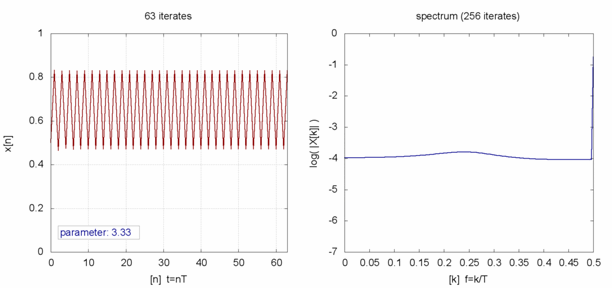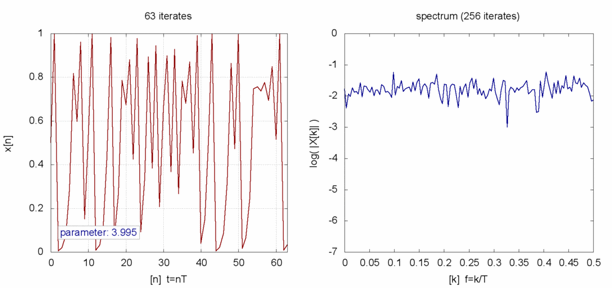
。在 ![]() 之時,『單峰映象』或快或慢的收斂到『零』;當
之時,『單峰映象』或快或慢的收斂到『零』;當 ![]() 之時,它很快的逼近
之時,它很快的逼近 ![]() ;於
;於 ![]() 之時,線性的上下震盪趨近
之時,線性的上下震盪趨近 ![]() ;雖然
;雖然 ![]() 也收斂到
也收斂到 ![]() ,然而已經是很緩慢而且不是線性的了;當
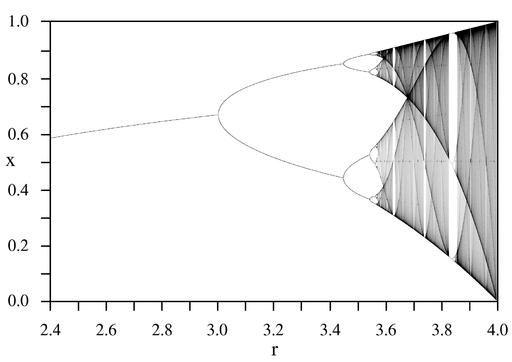
,然而已經是很緩慢而且不是線性的了;當 ![]() 時,對幾乎各個『初始條件』而言,系統開始發生兩值『震盪現象』,而後變成四值、八值、十六值…等等的『持續震盪』;最終於大約
時,對幾乎各個『初始條件』而言,系統開始發生兩值『震盪現象』,而後變成四值、八值、十六值…等等的『持續震盪』;最終於大約 ![]() 時,這個震盪現象消失了,系統就步入了所謂的『混沌狀態』的了!!
時,這個震盪現象消失了,系統就步入了所謂的『混沌狀態』的了!!
『連續的』微分方程式沒有『混沌性』,『離散的』差分方程式反倒發生了『混沌現象』,那麼這個『量子』的『宇宙』到底是不是『混沌』的呢??回想之前『λ 運算』裡的『遞迴函式』,與數學中的『定點』定義,『單峰映象』可以看成函數 ![]() 的『迭代求值』︰
的『迭代求值』︰![]() 。當
。當 ![]() ,這個
,這個 ![]() 就是『定點』,左圖中顯示出不同的
就是『定點』,左圖中顯示出不同的 ![]() 值的求解現象,從有『定點』向『震盪』到『混沌』。如果我們將『 logistic equation』改寫成
值的求解現象,從有『定點』向『震盪』到『混沌』。如果我們將『 logistic equation』改寫成 ![]() ,假使取
,假使取 ![]() ,可以得到
,可以得到 ![]() ,它的『極限值』
,它的『極限值』 ![]() ,根本與
,根本與 ![]() 沒有關係,這也就說明了兩者的『根源』是不同的啊!然而這卻建議著一種『時間序列』的觀點,如將
沒有關係,這也就說明了兩者的『根源』是不同的啊!然而這卻建議著一種『時間序列』的觀點,如將 ![]() 看成
看成 ![]() ,這樣
,這樣 ![]() 就說是『速度』的了,於是
就說是『速度』的了,於是 ![]() 便構成了假想的『相空間』,這可就把一個『遞迴關係式』轉譯成了一種『符號動力學』的了!!
便構成了假想的『相空間』,這可就把一個『遞迴關係式』轉譯成了一種『符號動力學』的了!!
在某些特定的 ![]() 值,這個『遞迴關係式』有『正確解』 exact solution,比方說
值,這個『遞迴關係式』有『正確解』 exact solution,比方說 ![]() 時,
時,![]() ,因為
,因為 ![]() ,所以
,所以 ![]() ,於是
,於是 ![]() ,因此
,因此 ![]() 。再者由於『指數項』
。再者由於『指數項』 ![]() 是『偶數』,所以此『符號動力系統』不等速 ── 非線性 ── 而且不震盪的逼近『極限值』的啊。
是『偶數』,所以此『符號動力系統』不等速 ── 非線性 ── 而且不震盪的逼近『極限值』的啊。
對於 ![]() 來講,它的解是
來講,它的解是
![]()
,此處 ![]() 是『初始條件』參數,可由
是『初始條件』參數,可由 ![]() 來決定。假使
來決定。假使 ![]() 是『有理數』,那麼
是『有理數』,那麼 ![]() 這個『周期函數』,多次『迭代』後就可能產生『極限循環』;要是
這個『周期函數』,多次『迭代』後就可能產生『極限循環』;要是 ![]() 是『無理數』,它有一個『不循環』的無窮小數成份,這個『符號動力系統』就彷彿是『隨機亂動』一般,因此才說它是『混沌』的啊!假使思考
是『無理數』,它有一個『不循環』的無窮小數成份,這個『符號動力系統』就彷彿是『隨機亂動』一般,因此才說它是『混沌』的啊!假使思考 ![]() 是一個『有理數』的機會,怕是很渺茫的吧!!
是一個『有理數』的機會,怕是很渺茫的吧!!
之後,有人『擴張』了 ![]() 方法的『解決範圍』,考慮了如下的方程式
方法的『解決範圍』,考慮了如下的方程式
![]() ,它的解是
,它的解是
![]() 。
。
並且探討了對於『整數』 ![]() ,當滿足
,當滿足 ![]() 『定點』時的『情況』,在此我們就不多說的了。一般來說『非線性』方程式﹐很少能夠有『正確解』,通常多半需要依賴『數值分析』工具去『了解』它的內蘊,在此再次提醒讀者『樹莓派』上的『Mathematica』的『實用性』,並且給出兩個相關的鍊結給有興趣的讀者
『定點』時的『情況』,在此我們就不多說的了。一般來說『非線性』方程式﹐很少能夠有『正確解』,通常多半需要依賴『數值分析』工具去『了解』它的內蘊,在此再次提醒讀者『樹莓派』上的『Mathematica』的『實用性』,並且給出兩個相關的鍊結給有興趣的讀者
【單峰映象】
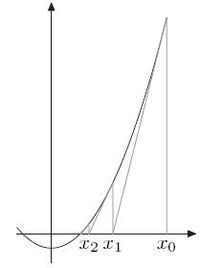
。即使當一個『多項式方程式』的『次方數』超過了『四階』都沒有『一般解』,於是科學上也常用著『牛頓法』或又稱之為『牛頓-拉弗森法』 Newton-Raphson method 來『求』 ![]() 的『解』,從『數值分析』上講,就是『求解』
的『解』,從『數值分析』上講,就是『求解』
![]() 的啊!假使說所『揣想』的『初始』答案
的啊!假使說所『揣想』的『初始』答案 ![]() 並不『適當』,難保不會發生前述的『各種現象』,那麼又該要怎麽『判斷』的呢??
並不『適當』,難保不會發生前述的『各種現象』,那麼又該要怎麽『判斷』的呢??