![]()
二零零一年加拿大傑夫‧塔珀 Jeff Tupper 所發現的自指公式,它的二維『函數圖像』,與數學的『公式外觀』相仿。
一九二九年比利時畫家雷內‧弗朗索瓦‧吉蘭‧馬格利特 René François Ghislain Magritte 名作《形象的叛逆》The Treachery of Images 上用法文寫著 『你看到的不是煙斗』。
一九零四年荷蘭著名品牌德羅斯特 Droste 所販售的可可粉之包裝盒上的圖片是一位護士拿著一個上有杯子及紙盒的托盤,托盤裡的杯子和紙盒上之圖案也就是這張圖片。
『抽象』的概念雖然『無象』可以用來作『想象』,就如同前面談到過的『思想實驗』一樣,還是可以建造『情境』方便『觀相』的。假使說『思考』是根『概念磁鐵』,那麼『思維』就是『磁力線』。從『創造發想』的『發散處』出發,抵達『清晰自恰』之『收斂點』。因此『磁力線』的『封閉性』也可比喻成『思維』是『自我遞迴』的了。這樣或許『思考』在『博』與『精』的方面能夠成為『自行車』之『雙輪』,而這個『操控』之人也逐漸地步上了『收發自如』的道路。
讓我們再次思考邱奇自然數的構造
![]()
![]()
![]()
,這說明了變元 ![]() 在結構中的位置,以及『應用求值策略』也許是『外到內』
在結構中的位置,以及『應用求值策略』也許是『外到內』![]() 或者是『內到外』
或者是『內到外』![]() 。當我們在『解讀』一個表達式時,什麼將會是『變元』
。當我們在『解讀』一個表達式時,什麼將會是『變元』![]() 的『賦值』,以及它們的『性質』,往往就是『理解』表達式的『關鍵處』,以及自己『構思』的『起始點』。舉個『ISZERO』例子說
的『賦值』,以及它們的『性質』,往往就是『理解』表達式的『關鍵處』,以及自己『構思』的『起始點』。舉個『ISZERO』例子說
![]()
![]()
![]()
![]()
![]()
![]()
,然而 ![]() ,這就是為什麼選擇『
,這就是為什麼選擇『 ![]() 』函式的原因。現在只剩下『0』的情況需要考慮了
』函式的原因。現在只剩下『0』的情況需要考慮了
![]()
![]()
![]()
![]()
![]()
,所以也就是會用『TRUE』的理由。
在數學上既然有『加法』也就有『減法』,那麼能不能仿造 ![]() 的『後繼數』是
的『後繼數』是 ![]() ,定義一個『前導數』predecessesor
,定義一個『前導數』predecessesor ![]() 的呢?也就是說在
的呢?也就是說在 ![]() 中想辦法『去掉一個
中想辦法『去掉一個 ![]() 』,下面的這個
』,下面的這個
![]()
就是一個精巧的設計。為了『解讀』這個設計,讓我們先定義幾個『縮寫』以利表達的『簡潔』︰
![]()
![]()
![]()
![]()
Lambda Calculator 化約例子
PRED 3
⇒ λf.λx.3 T D I
⇒ λf.λx.(λi0.T (T [T i0])) D I
3⇒ λf.λx.T (T (T D)) I
4⇒ λf.λx.(λh.h (T [T D] f)) I
5⇒ λf.λx.I (T (T D) f)
6⇒ λf.λx.T (T D) f
⇒ λf.λx.(λh.h (T D f)) f
⇒ λf.λx.f (T D f)
⇒ λf.λx.f ((λh.h [D f]) f)
⇒ λf.λx.f (f (D f))
⇒ 2
PRED 2
⇒ λf.λx.2 T D I
⇒ λf.λx.(λi0.T (T i0)) D I
3⇒ λf.λx.T (T D) I
4⇒ λf.λx.(λh.h (T D f)) I
5⇒ λf.λx.I (T D f)
6⇒ λf.λx.T D f
⇒ λf.λx.(λh.h (D f)) f
⇒ λf.λx.f (D f)
⇒ 1
PRED 1
⇒ λf.λx.1 T D I
⇒ λf.λx.(λi0.T i0) D I
3⇒ λf.λx.T D I
4⇒ λf.λx.(λh.h (D f)) I
5⇒ λf.λx.I (D f)
6⇒ λf.λx.D f
⇒ 0
PRED 0
⇒ λf.λx.0 T D I
⇒ λf.λx.I D I
3⇒ λf.λx.D I
⇒ 0
仔細觀察左邊化約例子的過程,我們可以說︰
甲、 ![]() 之主要目的就是『去掉一個
之主要目的就是『去掉一個 ![]() 』,它是一個值為變元
』,它是一個值為變元 ![]() 的『常函式』。
的『常函式』。
乙、 ![]() 的目的︰一、由於在自然數中並沒有『負數』的概念。在『PRED 0』中
的目的︰一、由於在自然數中並沒有『負數』的概念。在『PRED 0』中 ![]() ,所以『化約』依然為『0』,這至少是我們所期望的『結果』。二、化約過程的『第 3 步』是展開
,所以『化約』依然為『0』,這至少是我們所期望的『結果』。二、化約過程的『第 3 步』是展開 ![]() 最左邊的第一個
最左邊的第一個 ![]() ,這時
,這時 ![]() 中的變元
中的變元 ![]() 已經替換成
已經替換成 ![]() 所以得到
所以得到 ![]() 。假使沒有『 結尾』的
。假使沒有『 結尾』的 ![]() ,是化約不掉這一個變元
,是化約不掉這一個變元 ![]() 函式封裝,進行『第 4 步』的,它將於化約過程中『駐留』。又因為
函式封裝,進行『第 4 步』的,它將於化約過程中『駐留』。又因為 ![]() 是恆等函式
是恆等函式 ![]() ,所以才能夠得到『第 6 步』的
,所以才能夠得到『第 6 步』的 ![]() 。然後逐步化約透過
。然後逐步化約透過 ![]() 將
將 ![]() 個變元
個變元 ![]() 從『
從『![]() 』的右邊『複製』到『
』的右邊『複製』到『![]() 』之左邊,於是最終止於
』之左邊,於是最終止於 ![]() 的化約。『丟掉』了這個『
的化約。『丟掉』了這個『![]() 』,以及『保留』變元
』,以及『保留』變元 ![]() 完成了
完成了 ![]() 的『前導數』
的『前導數』![]() 之運算。
之運算。
讀者可以用 Lambda Calculator 多練習幾個例子,自己嘗試作一些『概念實驗』,細心體會一下『高階函式』運用的『巧妙處』。有時後用有意義的『單個符號』當作『運算子』,常常較容易『理解』與『運用』,因為這在『量子力學』中早已經行之多年的了。
既然已經有了『前導數』,我們就可以將『減法』 ![]() 定義成
定義成
![]()
。也就是說 ![]() 是自然數
是自然數 ![]() 『用前導數』
『用前導數』 ![]() 次的那個數。在《λ 運算︰概念導引之《補充》※真假祇是個選擇??》一文中,我們談到過一些『邏輯』運算的定義。比方說藉著『非』NOT 、『ISZERO』 和『減法』,我們可以將自然數之『大於』關係
次的那個數。在《λ 運算︰概念導引之《補充》※真假祇是個選擇??》一文中,我們談到過一些『邏輯』運算的定義。比方說藉著『非』NOT 、『ISZERO』 和『減法』,我們可以將自然數之『大於』關係 ![]() 定義為
定義為
![]()
。這是為什麼呢?因為假使 ![]() ,那麼
,那麼 ![]() ,所以
,所以 ![]() 為假,因此
為假,因此 ![]() 就為真。有人說萬一
就為真。有人說萬一 ![]() ,這時根據『PRED』的定義,因此
,這時根據『PRED』的定義,因此 ![]() 為『0』,所以
為『0』,所以 ![]() 為真,那麼
為真,那麼 ![]() 就為假。
就為假。
當然自然數的『等於』與『小於』關係也都是可以『定義』的,於此就不一一介紹的了。不如列出作者驗證文本『正確與否』用的一些 Lambda Calculator 『字典定義』,提供有興趣的讀者研究︰
* [\m.\n.m (+ n) 0] = \m.\n.m (\i0.\f.\x.n f (i0 f x)) FALSE
+ [\m.\n.\f.\x.m f (n f x)] = \m.\n.\f.\x.m f (n f x)
– [\n. \m. m PRED n] = \n.\m.m PRED n
0 [\f.\x.x] = \f.\x.x
1 [SUCC 0] = \f.\x.f x
2 [SUCC 1] = \f.\x.f (f x)
3 [SUCC 2] = \f.\x.f (f (f x))
4 [SUCC 3] = \f.\x.f (f (f [f x]))
5 [SUCC 4] = \f.\x.f (f (f [f (f x)]))
6 [SUCC 5] = \f.\x.f (f (f [f (f (f x))]))
7 [SUCC 6] = \f.\x.f (f (f [f (f (f {f x}))]))
8 [SUCC 7] = \f.\x.f (f (f [f (f (f {f (f x)}))]))
9 [SUCC 8] = \f.\x.f (f (f [f (f (f {f (f (f x))}))]))
< [\m. \n. AND (ISZERO (- m n)) (NOT(ISZERO (- n m)))] = \m.\n.n PRED m (\x.FALSE) TRUE (m PRED n (\x.FALSE) TRUE FALSE TRUE) FALSE
= [\m. \n. AND (ISZERO (- m n)) (ISZERO (- n m))] = \m.\n.n PRED m (\x.FALSE) TRUE (m PRED n (\x.FALSE) TRUE) FALSE
> [\m. \n. NOT (ISZERO (- m n))] = \m.\n.n PRED m (\x.FALSE) TRUE FALSE TRUE
AND [\p. \q. p q FALSE] = \p.\q.p q FALSE
FALSE [\x.\y.y] = \x.\y.y
IFTHENELSE [\p. \x. \y. p x y] = \p.\x.\y.p x y
ISZERO [\n.n(\x.FALSE) TRUE] = \n.n (\x.FALSE) TRUE
NOT [\p. p FALSE TRUE] = \p.p FALSE TRUE
OR [\p. \q. p TRUE q] = \p.\q.p TRUE q
PRED [\n. \f. \x. n (\g. \h. h (g f)) (\u.x)(\u.u)] = \n.\f.\x.n (\g.\h.h (g f)) (\u.x) (\u.u)
SUCC [\n.\f.\x.f(n f x)] = \n.\f.\x.f (n f x)
TRUE [\x.\y.x] = \x.\y.x
Y [\g. (\x. g(x x)) (\x. g(x x))] = \g.(\x.g (x x)) (\x.g (x x))
g [\f. \n. IFTHENELSE (ISZERO n) (SUCC 0) (+ n (f ( PRED n)) )] = \f.\n.n (\x.FALSE) TRUE 1 (\i0.\x.n i0 (f [\i1.\i2.n (\g.\h.h (g i1)) (\u.i2) (\u.u)] i0 x))
h [\f. \n. IFTHENELSE (ISZERO n) (SUCC 0) (@ n (f ( PRED n)) )] = \f.\n.n (\x.FALSE) TRUE 1 (@ n (f [\i0.\x.n (\g.\h.h (g i0)) (\u.x) (\u.u)]))
既然談『λ 運算』表達式,如果不講『遞迴』函式;就彷彿是人到了『巴黎』,卻又沒見着『艾菲爾鐵塔』。之前在《自我再現》中提到函數 ![]() 之『定點』的定義是
之『定點』的定義是 ![]() ,此時
,此時 ![]() 。然而『 λ 表達式』無法『直接』的『自我指涉』。有人問為什麼呢?回顧一下它的『定義』,每一個寫出來的表達式都是『匿名的』,如果連『名字』都沒有,又怎麼能夠『指涉其名』的呢?所以只能『迂迴』的『間接』透過其它函式來『指涉』所說的就是那個『匿名的□□』。就像『自我應用』組合子,在函式應用時,可以產生『自我作用』一樣。著名的哈斯凱爾‧卡瑞 Haskell Brooks Curry ── 組合邏輯的發展者,Haskell 與 Brooks 程式語言都用他的名字來命名 ──,發現了『
。然而『 λ 表達式』無法『直接』的『自我指涉』。有人問為什麼呢?回顧一下它的『定義』,每一個寫出來的表達式都是『匿名的』,如果連『名字』都沒有,又怎麼能夠『指涉其名』的呢?所以只能『迂迴』的『間接』透過其它函式來『指涉』所說的就是那個『匿名的□□』。就像『自我應用』組合子,在函式應用時,可以產生『自我作用』一樣。著名的哈斯凱爾‧卡瑞 Haskell Brooks Curry ── 組合邏輯的發展者,Haskell 與 Brooks 程式語言都用他的名字來命名 ──,發現了『![]() 』組合子,現今稱作『Curry 之悖論組合子』。為什麼要叫做『悖論』的呢?因為『自我指涉』恐怕會產生『羅素悖論』之故!但是『
』組合子,現今稱作『Curry 之悖論組合子』。為什麼要叫做『悖論』的呢?因為『自我指涉』恐怕會產生『羅素悖論』之故!但是『 ![]() 組合子』雖可能會『陷入』無窮推導,卻沒有『矛盾』,它的一個特性,就是使用『 λ 表達式』做『遞迴的關鍵』︰
組合子』雖可能會『陷入』無窮推導,卻沒有『矛盾』,它的一個特性,就是使用『 λ 表達式』做『遞迴的關鍵』︰
![]()
,比對『定點』的定義,就可以知道函式應用 ![]() 是變元函式
是變元函式 ![]() 的『定點函式』,也就是說『藉著
的『定點函式』,也就是說『藉著 ![]() 』,將一個命名的變元函式
』,將一個命名的變元函式 ![]() 轉成了『自我調用』。為了避免
轉成了『自我調用』。為了避免 ![]() 的『無窮推導』,就像數學裡『迴歸定義』一樣,總要有一個『中止條件』。假使
的『無窮推導』,就像數學裡『迴歸定義』一樣,總要有一個『中止條件』。假使
![]()
,如果定義的自然數二元運算 ![]() 類似具有『加法』或『乘法』的性質,
類似具有『加法』或『乘法』的性質,![]() 的結果就是
的結果就是
![]()
,這個 ![]() 就是使用『 λ 表達式』寫作『遞迴函式』的一般範例,而
就是使用『 λ 表達式』寫作『遞迴函式』的一般範例,而 ![]() 就是『中止條件』的化約『傳回值』。
就是『中止條件』的化約『傳回值』。
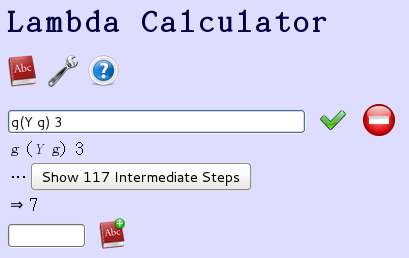
由於 Lambda Calculator 預設的『最大化約步驟』是兩百步,所以作者沒有給『階乘』![]() 的例子,讀者可以自己寫。左圖一是『字典表列』中有的
的例子,讀者可以自己寫。左圖一是『字典表列』中有的 ![]() ,它是『連加法』,中止條件是
,它是『連加法』,中止條件是 ![]() ,所以
,所以 ![]() 的計算結果是
的計算結果是 ![]() 。
。
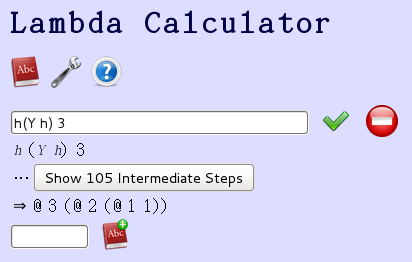
左圖二中叫做『![]() 』的其實就是那個『
』的其實就是那個『![]() 』,它的中止條件是
』,它的中止條件是 ![]() ,並將二元運算符號由
,並將二元運算符號由 ![]() 改成了『@』。為什麼『初始值』都不用『0』的呢?其實這樣做是為了『測試』演算法,有沒有『打錯字』以及『0』的表達式有『多義性』而考慮的。
改成了『@』。為什麼『初始值』都不用『0』的呢?其實這樣做是為了『測試』演算法,有沒有『打錯字』以及『0』的表達式有『多義性』而考慮的。
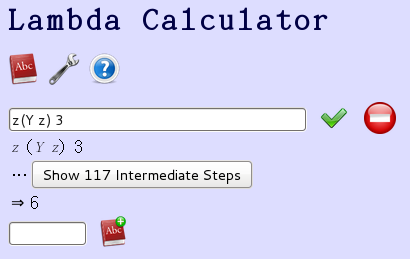
左圖三計算 ![]() ,
,![]() 函式如同上面的
函式如同上面的 ![]() 函式一樣,但是它的初始值就是『0』。
函式一樣,但是它的初始值就是『0』。
傳說中講『西楚霸王』項羽,不只是『力拔山兮,氣蓋世!』,更神奇的是︰自己還能『舉起自己』,但是依據『牛頓作用反作用力定律』這是『可能』的嗎??