過去我們曾經談及『二項分佈』,並且推導它與『卜瓦松分佈』的關係︰
擲一個硬幣產生『正‧反』面兩種結果,這是很普通的現象,今天在『術語』上稱之為『伯努利試驗』Bernoulli trial,是說對一個只有兩種可能結果的單次『隨機試驗』,就一個『隨機變數』 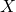 而言,
而言,
![Rendered by QuickLaTeX.com Pr[X = 1] \ = \ p](http://www.freesandal.org/wp-content/ql-cache/quicklatex.com-9343f7df370d1e51787a88d7cdff18ed_l3.png)
![Rendered by QuickLaTeX.com Pr[X = 0] \ = \ 1-p = q](http://www.freesandal.org/wp-content/ql-cache/quicklatex.com-dec4972a4a8e92da1fdb6a1e6c810d82_l3.png)
,此處 ![Rendered by QuickLaTeX.com {Pr}_i[X_i = {\alpha}_i] = q_i](http://www.freesandal.org/wp-content/ql-cache/quicklatex.com-6f2da4060b11a0529c27c1ece41cfab5_l3.png) 是說『隨機變數』
是說『隨機變數』 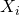 有
有 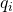 的機會取
的機會取 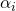 的值。從『期望值』的角度講
的值。從『期望值』的角度講
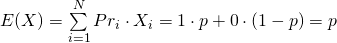
,它的『標準差』 Standard Deviation 是
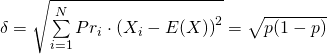
。這為什麼要叫做『伯努利試驗』的呢?一七三零年代,荷蘭出生大部分時間居住在瑞士巴塞爾的丹尼爾‧伯努利 Daniel Bernoulli 之堂兄尼古拉一世‧伯努利 Nikolaus I. Bernoulli,在致法國數學家皮耶‧黑蒙‧德蒙馬特 Pierre Rémond de Montmort 的信件中,提出了一個問題:擲 一枚硬幣,假使第一次擲出正面,你就賺了 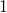 元。如果第一次出現反面,那就要再擲一次,若是第二次擲的是正面,你便賺了
元。如果第一次出現反面,那就要再擲一次,若是第二次擲的是正面,你便賺了 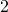 元。要是第二次擲出反面,那就得要擲第三次,假若第三次擲的是正面,你便賺
元。要是第二次擲出反面,那就得要擲第三次,假若第三次擲的是正面,你便賺 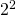 元……如此類推,也就是說你可能擲一次遊戲就結束了,也許會反覆擲個沒完沒了。問題是,你最多肯付多少錢來玩這個遊戲的呢?假使從『期望值』來考量,這個遊戲的期望值是『無限大』
元……如此類推,也就是說你可能擲一次遊戲就結束了,也許會反覆擲個沒完沒了。問題是,你最多肯付多少錢來玩這個遊戲的呢?假使從『期望值』來考量,這個遊戲的期望值是『無限大』
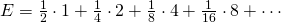
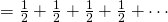
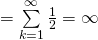
,然而即使你願意付出『無限的金錢』去參與這個遊戲。不過,你卻可能只賺到 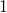 元,或
元,或 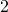 元,或
元,或 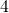 元……等等,只怕不可能賺到無限的金錢。那你又為什麼肯付出巨額的金錢加入遊戲的呢?
元……等等,只怕不可能賺到無限的金錢。那你又為什麼肯付出巨額的金錢加入遊戲的呢?
其後丹尼爾‧白努利於一七三八年寫了一篇論文『風險度量的新理論之討論』考慮了一個對等的遊戲,不斷的擲同一枚硬幣,直到獲得正面為止,如果你擲了 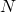 次才最終得到正面,你將獲得
次才最終得到正面,你將獲得 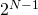 元。即使參與玩這個遊戲的花費是『天價』,假使我們考慮到這個遊戲的『期望收益』是無窮大,我們就應該參加。這就是史稱的『聖彼得堡悖論』。白努利提出了一個理論來解釋這個悖論,他得到了一條原理,『財富越多人越滿足,然而隨著財富的累積,滿足程度的增加率卻不斷下降』。這或許可以說是古典的『邊際效用遞減』版本,就像『白手起家』和其後之『錦上添花』,對一個人的『效用』之『滿足』是完全不同的一樣。他這麼講︰
元。即使參與玩這個遊戲的花費是『天價』,假使我們考慮到這個遊戲的『期望收益』是無窮大,我們就應該參加。這就是史稱的『聖彼得堡悖論』。白努利提出了一個理論來解釋這個悖論,他得到了一條原理,『財富越多人越滿足,然而隨著財富的累積,滿足程度的增加率卻不斷下降』。這或許可以說是古典的『邊際效用遞減』版本,就像『白手起家』和其後之『錦上添花』,對一個人的『效用』之『滿足』是完全不同的一樣。他這麼講︰
【邊際效用遞減原理】:一個人對於財富的佔有多多益善,就是說『效用函數』一階導數大於零;隨著財富的增加,滿足程度的增加速度不斷下降,正因為『效用函數』二階導數小於零。
【最大效用原理】:在『風險』和『不確定』的條件下,一個人行為的『決策準則』是為了獲得最大『期望效用』值而不是最大『期望金額』值。
作者不知『理性』是否該『相信』期望值,或者『感性』果就會『追求』效用量,彷彿『天下』到底是『患寡』還是『患不均』的呢??
事實上一個『發生』或『不發生』,『存在』也許『不存在』,是『成功』還是『失敗』的『可‧不可』 Yes or No 的『事件機率』能夠表達的『現象界』不勝枚舉,就像『德汝德模型』中『電子』之『碰撞』與『不碰撞』也是一樣的。假使我們將『伯努利試驗』推廣到 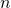 次中有
次中有 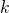 次的『成功率』,我們就得到了數學上所謂的『二項分佈』
次的『成功率』,我們就得到了數學上所謂的『二項分佈』
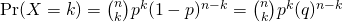
,此處 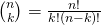 是
是 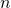 中取
中取 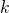 之『組合數』。假使
之『組合數』。假使 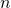 很大,且機率
很大,且機率 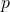 很小,這個『二項分佈』可以『近似』如下︰
很小,這個『二項分佈』可以『近似』如下︰
如果 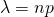 是有限大小的『適度量』,回顧指數函數
是有限大小的『適度量』,回顧指數函數  的定義之一是
的定義之一是
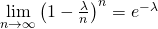
依據二項分佈的定義:
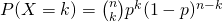
如果假設 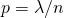 ,當
,當 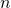 趨於無窮時,
趨於無窮時, 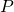 的極限可以如此計算
的極限可以如此計算
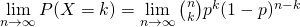
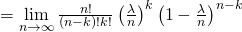
![Rendered by QuickLaTeX.com =\lim \limits_{n\to\infty} \underbrace{\left[\frac{n!}{n^k\left(n-k\right)!}\right]}_F \left(\frac{\lambda^k}{k!}\right) \underbrace{\left(1-\frac{\lambda}{n}\right)^n}_{\to\exp\left(-\lambda\right)} \underbrace{\left(1-\frac{\lambda}{n}\right)^{-k}}_{\to 1}](http://www.freesandal.org/wp-content/ql-cache/quicklatex.com-f16abcae54bf5047a0eea7c5c1b79a53_l3.png)
![Rendered by QuickLaTeX.com = \lim \limits_{n\to\infty} \underbrace{\left[ \left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right) \ldots \left(1-\frac{k-1}{n}\right) \right]}_{\to 1} \left(\frac{\lambda^k}{k!}\right) \underbrace{\left(1-\frac{\lambda}{n}\right)^n}_{\to\exp\left(-\lambda\right)} \underbrace{\left(1-\frac{\lambda}{n}\right)^{-k}}_{\to 1}](http://www.freesandal.org/wp-content/ql-cache/quicklatex.com-f9a1ceb4a6c8ec5597d00366fd3a1e11_l3.png)
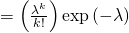
。這就是知名的 『卜瓦松分佈』 Poisson distribution,是法國數學家西莫恩‧德尼‧卜瓦松 Siméon-Denis Poisson 在一八三七年『Research on the Probability of Judgments in Criminal and Civil Matters』論文中最早先發表。『卜瓦松分佈』適合於描述單位時間內『隨機事件』發生之次數的『機率分佈』 ── 諸如某種服務在一定時間內所接到的服務請求人數,電話交換機需要轉接的來電次數、公汽站台裡的候車人數、一台機器會出現的故障率、自然災害發生的頻率、DNA 序列的變異數、放射性原子核的衰變係數等等 ──。它有兩個基本性質︰
一、滿足『卜瓦松分佈』的『隨機變數』,它的『期望值』與『變異數』 Variance ── 在此等於『標準差』的平方 ── 相等,都是『參數』 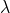 ,
, ![Rendered by QuickLaTeX.com E[X] = Var[X] = \lambda](http://www.freesandal.org/wp-content/ql-cache/quicklatex.com-114a238bf3f7e8cd1dffe8882e2bc725_l3.png) 。
。
二、兩個獨立而且滿足『卜瓦松分佈』之『隨機變數』,它們的『和』依然滿足『卜瓦松分佈』。
─── 引自《【Sonic π】電路學之補充《一》》
事實上這個『二項分佈』也是通往『常態分佈』的大門︰
正態近似
如果 n 足夠大,那麼分布的偏度就比較小。在這種情況下,如果使用適當的連續性校正,那麼 B(n, p) 的一個很好的近似是常態分布

n 越大(至少 20 ),近似越好,當 p 不接近 0 或 1 時更好。[5]不同的經驗法則可以用來決定 n 是否足夠大,以及 p 是否距離 0 或 1 足夠遠:
- 一個規則是 x=np 和 n(1 − p) 都必須大於 5 。
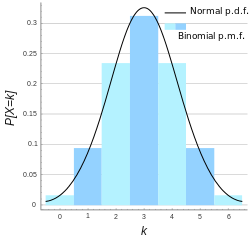
n = 6、p = 0.5 時的二項分布以及正態近似
於是人們逐步知道了
中央極限定理是機率論中的一組定理。中央極限定理說明,大量相互獨立的隨機變量,其均值的分布以常態分布為極限。這組定理是數理統計學和誤差分析的理論基礎,指出了大量隨機變量之和近似服從常態分布的條件。
歷史
Tijms (2004, p.169) 寫到:
中央極限定理有著有趣的歷史。這個定理的第一版被
法國數學家棣莫弗發現,他在 1733 年發表的卓越論文中使用
常態分布去估計大量拋擲硬幣出現正面次數的分布。這個超越時代的成果險些被歷史遺忘,所幸著名法國數學家
拉普拉斯在 1812 年發表的巨著
Théorie Analytique des Probabilités 中拯救了這個默默無名的理論。
拉普拉斯擴展了
棣莫弗的理論,指出二項分布可用常態分布逼近。但同
棣莫弗一樣,
拉普拉斯的發現在當時並未引起很大反響。直到十九世紀末中央極限定理的重要性才被世人所知。 1901 年,俄國數學家
里雅普諾夫用更普通的隨機變量定義中央極限定理並在數學上進行了精確的證明。如今,中央極限定理被認為是(非正式地)
機率論中的首席定理。
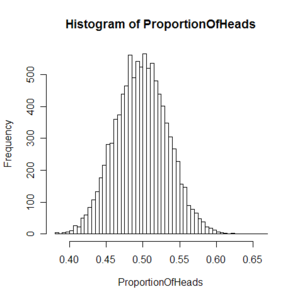
本圖描繪了多次拋擲硬幣實驗中出現正面的平均比率,每次實驗均拋擲了大量硬幣。
,深入瞭解了
在數學與統計學中,大數定律又稱大數法則、大數律,是描述相當多次數重複實驗的結果的定律。根據這個定律知道,樣本數量越多 ,則其平均就越趨近期望值。
大數定律很重要,因為它「保證」了一些隨機事件的均值的長期穩定性。人們發現,在重複試驗中,隨著試驗次數的增加,事件發生的頻率趨於一個穩定值;人們同時也發現,在對物理量的測量實踐中,測定值的算術平均也具有穩定性。比如,我們向上拋一枚硬幣 ,硬幣落下後哪一面朝上本來是偶然的,但當我們上拋硬幣的次數足夠多後,達到上萬次甚至幾十萬幾百萬次以後,我們就會發現 ,硬幣每一面向上的次數約占總次數的二分之一。偶然必然中包含著必然。
切比雪夫定理的一個特殊情況、辛欽定理和伯努利大數定律都概括了這一現象,都稱為大數定律。
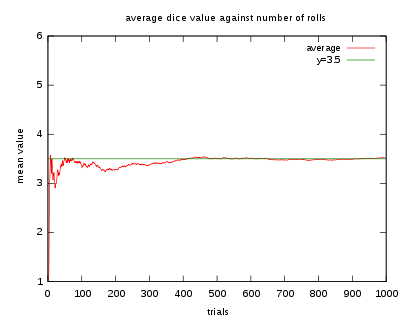
以特定擲單個骰子的過程來展示大數定律。隨著投擲次數的增加,所有結果的均值趨於 3.5(骰子點數的期望值)。不同時候做的這個實驗會在投擲數量較小的時候(左部)會表現出不同的形狀,當數量變得很大(右部)的時候,它們將會非常相似。
從此為『量測數據』之『分析』與『處理』奠定了基礎。
在『統計推理 』的輔翼下,那古典的『勞侖茲振子』模型,將使『燭龍』繼續光照大地的耶??!!
今天人們用著『勞侖茲振子』模型結合『統計力學』,來解釋許多大自然『物理現象』的『成因』。根據美國太空總署二零零七年『瑟宓斯衛星任務』 Themis mission 傳回的新數據,科學家發現『太陽』釋放的『帶電粒子』像一道氣流飛向地球,碰到『兩極上空磁場』時又形成若干『扭曲磁場』,因此『帶電粒子』的能量在『瞬間釋放』, 並以燦爛眩目的『北極光』形式『呈現』。然而地球上的極光主要只有『紅、綠』二色是因為在『熱成層』的『氮氣』和『氧氣』原子被『電子』碰撞後,各自散發出『紅色』或『綠色』的色光之故。
既然『電磁波』是『波』,一定有『折射』與『反射』的現象,然而從『微觀』的角度來看『巨觀』的『介質』,這可能是『完全不相同』的事情。好比說『理想氣體』方程式所講的『溫度』、『壓力』與『體積』等等的『巨觀量』,其實可以說是『微觀』中『各方向難以計數』之粒子作『彈性碰撞』的『解釋』一樣。因此從『物理理論』之『概念』來講是不是『折射率』也有一個『由來』的呢?舉例來說所謂『電磁波』的『折射定律』是否『邏輯上』能從馬克思威的『電磁理論』推導出來的呢??或許這也正是『勞侖茲』想要解答的『問題』之一;也許他果然是『受限』於他的時代,但是他的『模型』卻超越了他的『時代』;現今來講人們可以用著『勞侖茲振子』以及『量子統計力學』不只『解釋』那個『折射率』的問題,它還可以說明『吸收率』與『色散性』種種的『成因』。
自然的『奧妙』常在於『最普通』的現象,就像大部分物質都會『熱脹冷縮』,然而『水』結冰時卻是『體積膨脹』,這使得它的『密度下降』,或可以浮之於水上,難到它不是也保護了『水下生物』得以『保持生機』以至於『過冬』的嗎 ?更不要講大氣最外的『臭氧層』 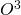 到底怎麽回事的了??
到底怎麽回事的了??
─── 引自《【Sonic π】聲波之傳播原理︰共振篇《三上》》

0 - 65^{\circ} C \ \pm 2^{\circ} C
0 - 60^{\circ} C \ \pm 1^{\circ} C
\Box = \alpha \cdot \bigcirc + \beta
\sigma_{\Box} = \alpha \cdot \sigma_{\bigcirc}
python3 Python 3.4.2 (default, Oct 19 2014, 13:31:11) [GCC 4.9.1] on linux Type "help", "copyright", "credits" or "license" for more information. >>> from sense_hat import SenseHat >>> 感測 = SenseHat() >>> 溫度 = 感測.get_temperature() >>> 壓力 = 感測.get_pressure() >>> 溼度 = 感測.get_humidity() >>> 溫度 = round(溫度, 1) >>> 壓力 = round(壓力, 1) >>> 溼度 = round(溼度, 1) >>> print(溫度, 壓力, 溼度) 27.9 1017.3 67.5 >>>
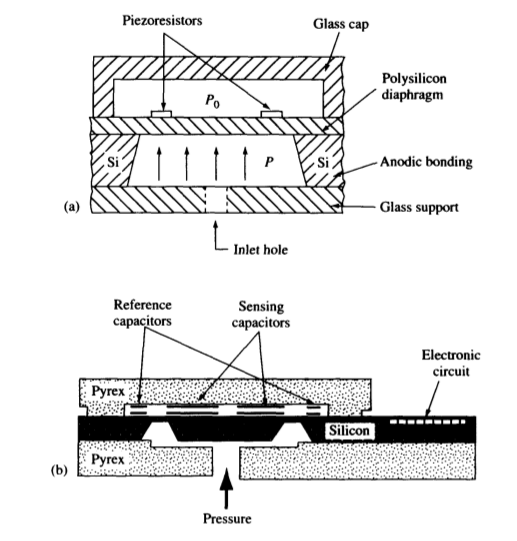

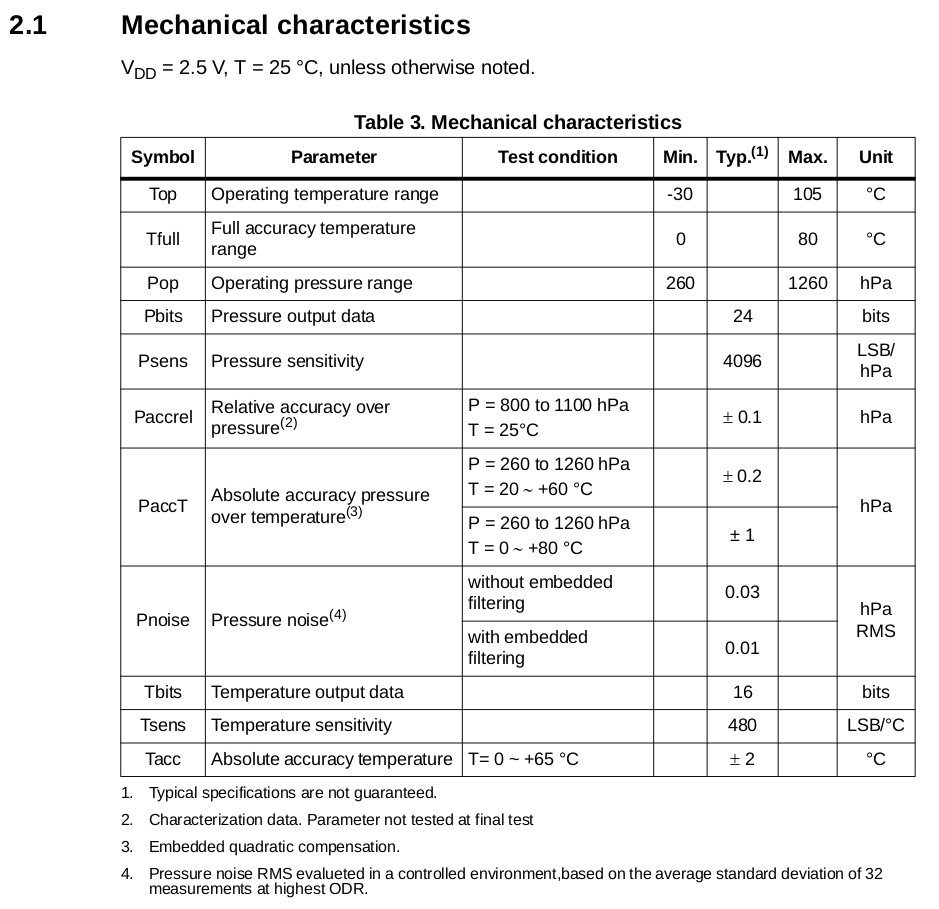

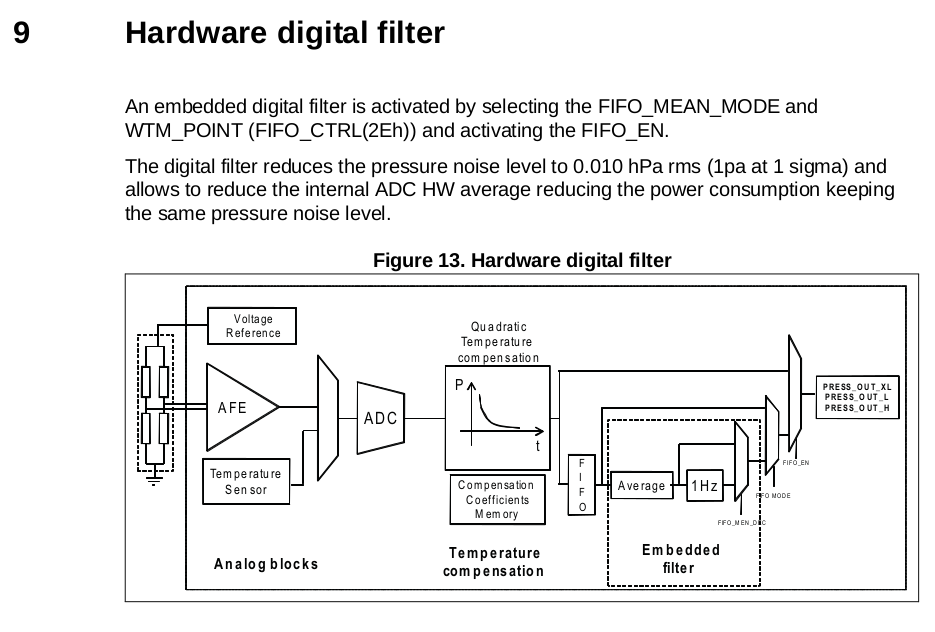
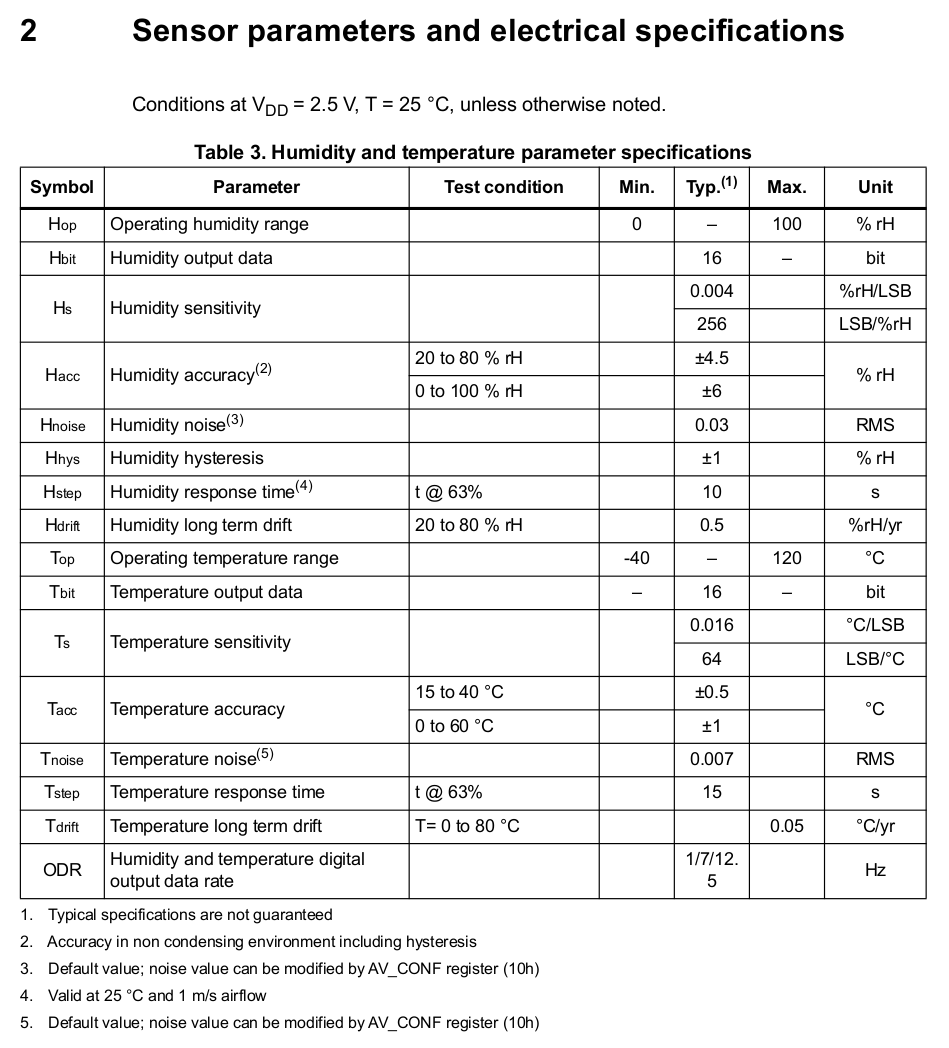

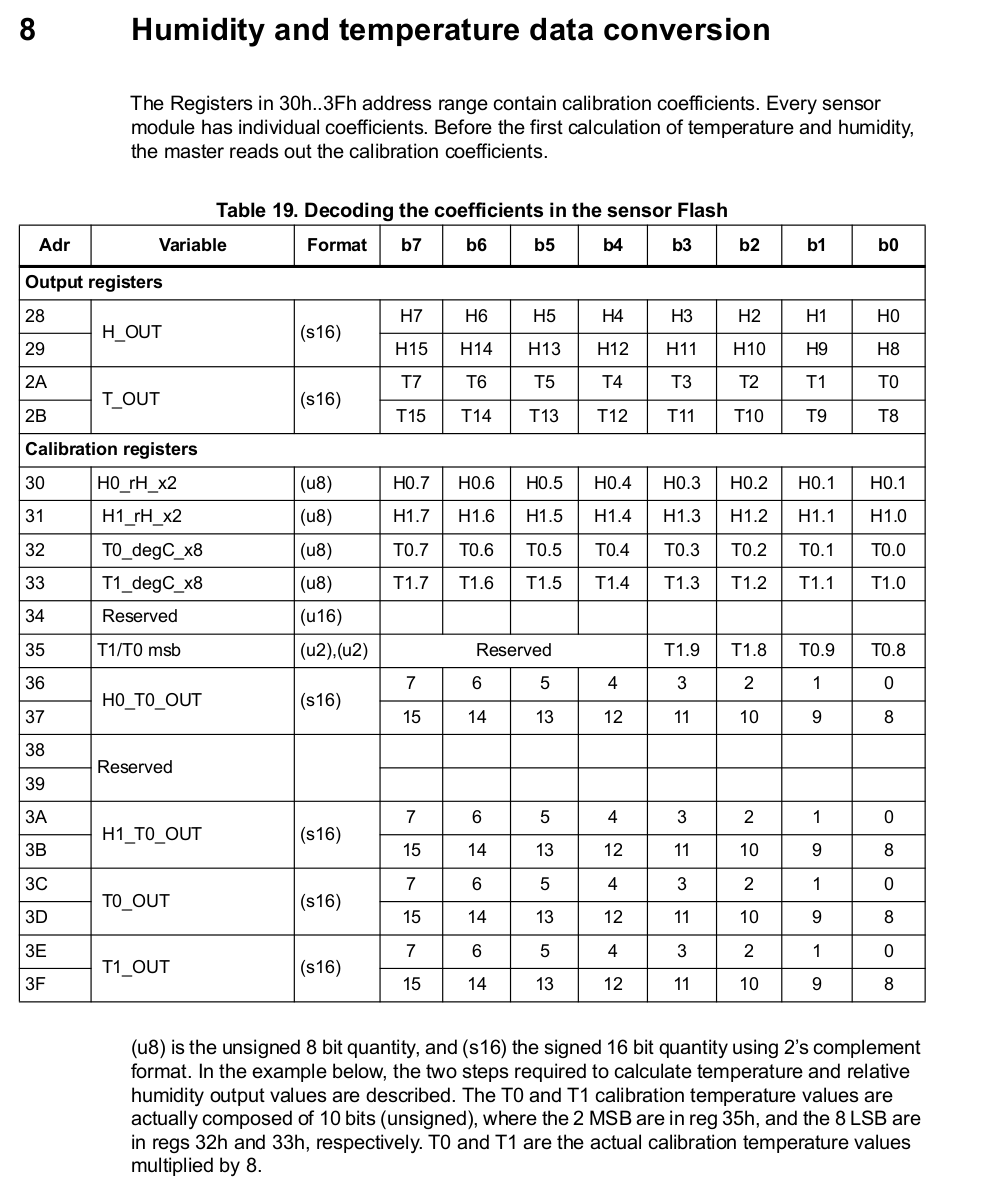
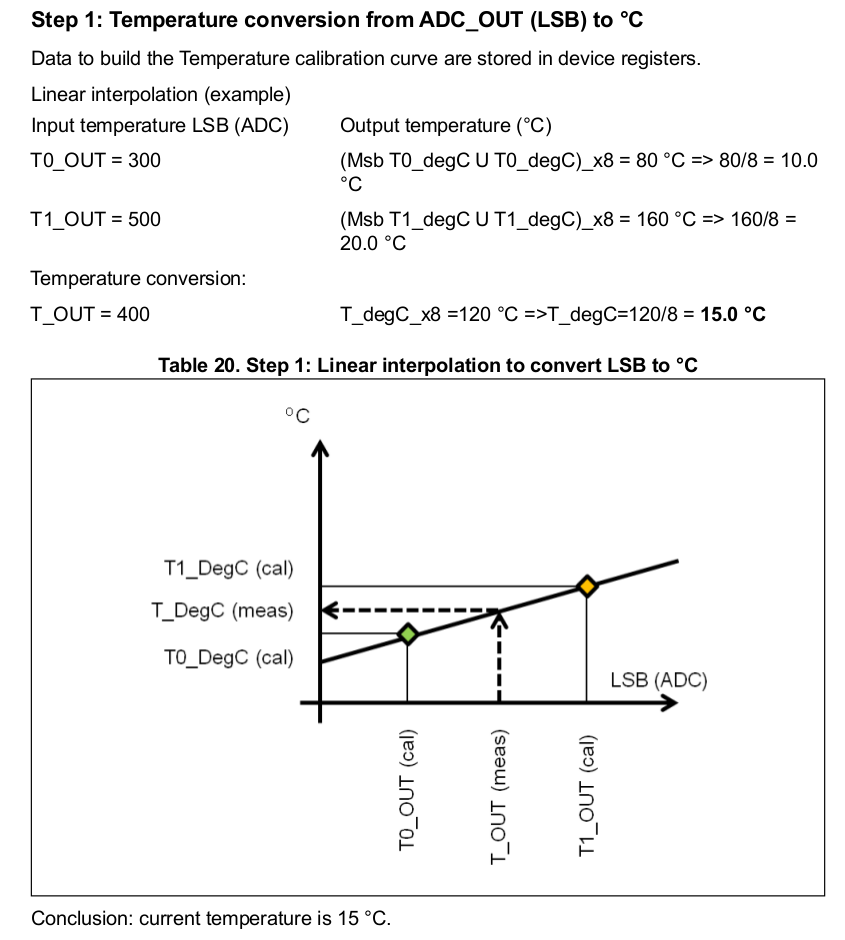





 ,
, ,
, 稱為
稱為 

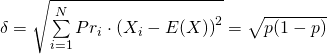
![Rendered by QuickLaTeX.com =\lim \limits_{n\to\infty} \underbrace{\left[\frac{n!}{n^k\left(n-k\right)!}\right]}_F \left(\frac{\lambda^k}{k!}\right) \underbrace{\left(1-\frac{\lambda}{n}\right)^n}_{\to\exp\left(-\lambda\right)} \underbrace{\left(1-\frac{\lambda}{n}\right)^{-k}}_{\to 1}](http://www.freesandal.org/wp-content/ql-cache/quicklatex.com-f16abcae54bf5047a0eea7c5c1b79a53_l3.png)
![Rendered by QuickLaTeX.com = \lim \limits_{n\to\infty} \underbrace{\left[ \left(1-\frac{1}{n}\right)\left(1-\frac{2}{n}\right) \ldots \left(1-\frac{k-1}{n}\right) \right]}_{\to 1} \left(\frac{\lambda^k}{k!}\right) \underbrace{\left(1-\frac{\lambda}{n}\right)^n}_{\to\exp\left(-\lambda\right)} \underbrace{\left(1-\frac{\lambda}{n}\right)^{-k}}_{\to 1}](http://www.freesandal.org/wp-content/ql-cache/quicklatex.com-f9a1ceb4a6c8ec5597d00366fd3a1e11_l3.png)