每日彙整: 2016-12-18

樹莓派、樹莓派之學習、樹莓派之教育

L4K ︰小海龜繪圖《II》

傳統上 Logo 的精神強調自己『動手作』，從經驗中學習『編程』。雖說作者不知為何畫 □

TO SQUARE

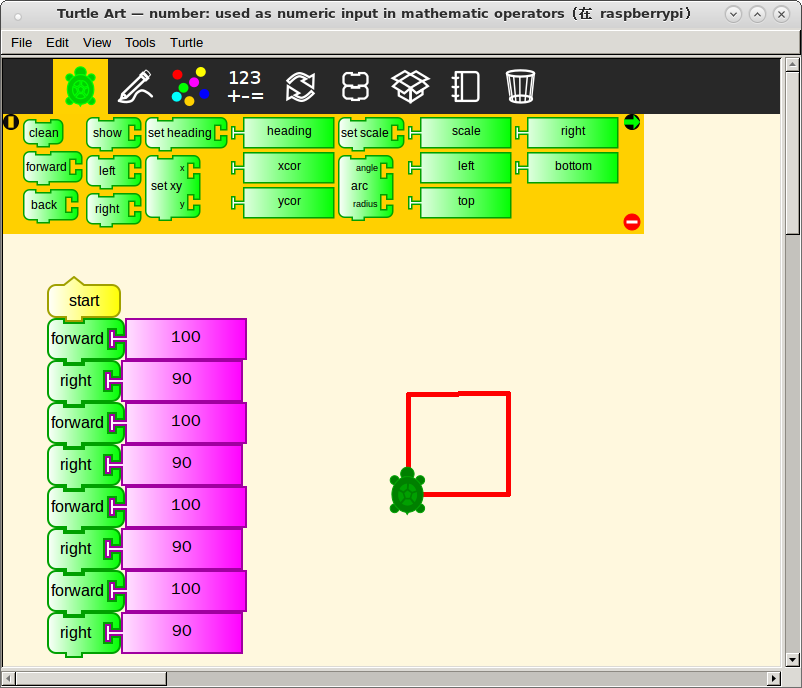
The traditional introduction to Logo has been to draw a square. Often times when running a workshop, I have the learners form a circle around one volunteer, the “turtle”, and invite them to instruct the turtle to draw a square. (I coach the volunteer beforehand to take every command literally, as does our graphical turtle.) Eventually the group converges on “go forward some number of steps”, “turn right (or left) 90 degrees”, “go forward some number of steps”, “turn right (or left) 90 degrees”, “go forward some number of steps”, “turn right (or left) 90 degrees”, “go forward some number of steps”. It is only on rare occasions that the group includes a final “turn right (or left) 90 degrees” in order to return the turtle to its original orientation. At this point I introduce the concept of “repeat” and then we start in with programming with Turtle Blocks.

 

turtle-art-number-used-as-numeric-input-in-mathematic-operators

 

成了『打招呼』 hello, world 的程式︰

一九七二年布萊恩‧柯林漢 Brian Wilson Kernighan  於貝爾實驗室撰寫《Introduction to the Language B》的內部技術文件時，寫了一個『hello, world』的範例程式。其後他與 丹尼斯‧里奇 Dennis M. Ritchie 合著的《The C Programming Language》也保留了這個範例程式。不知怎的這成了一個『傳統』，成了初學者所編寫的第一個程式。現今流行的寫法是『Hello, World!』，不知柯林漢會不會抱怨這是是那個嗎？它的原典是︰

hello, world

，裡頭所有字母全是小寫，『 , 』之後有一『空白』。

─── 摘自《Thue 之改寫系統《三》》

 

但思如從『語言』的角度來看『積木』，要只是用

forward  向前

right  右轉

left  左轉

number   數值

 

堆積一次一次的『重複』︰

forward-100

right-90

 

未免無趣哉？？如是畫 ☆ 以及於『正多邊形』之程式︰

Regular polygon

In Euclidean geometry, a regular polygon is a polygon that is equiangular (all angles are equal in measure) and equilateral (all sides have the same length). Regular polygons may be convex or star. In the limit, a sequence of regular polygons with an increasing number of sides becomes a circle, if the perimeter is fixed, or a regular apeirogon, if the edge length is fixed.

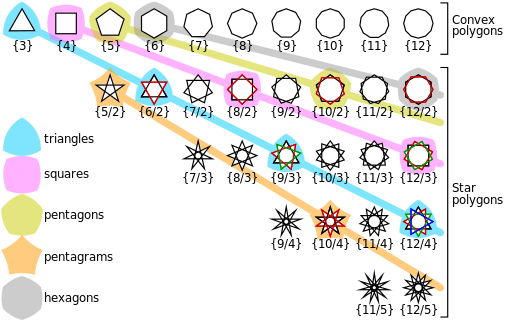
regular_star_polygons-svg

Regular convex and star polygons with 3 to 12 vertices labelled with their Schläfli symbols

……

Regular convex polygons

All regular simple polygons (a simple polygon is one that does not intersect itself anywhere) are convex. Those having the same number of sides are also similar.

An n-sided convex regular polygon is denoted by its Schläfli symbol {n}. For n < 3 we have two degenerate cases:

  • Monogon {1}: degenerate in ordinary space. (Most authorities do not regard the monogon as a true polygon, partly because of this, and also because the formulae below do not work, and its structure is not that of any abstract polygon.)
  • Digon {2}: a “double line segment”: degenerate in ordinary space. (Some authorities do not regard the digon as a true polygon because of this.)

In certain contexts all the polygons considered will be regular. In such circumstances it is customary to drop the prefix regular. For instance, all the faces of uniform polyhedra must be regular and the faces will be described simply as triangle, square, pentagon, etc.

Angles

For a regular convex n-gon, each interior angle has a measure of:

  \left(1-\frac{2}{n}\right)\times 180\,\,\, degrees, or equivalently(n-2)\times {\frac {180}{n}} degrees,
or {\frac {(n-2)\pi }{n}} radians,
or  {\frac {(n-2)}{2n}} full turns,

and each exterior angle (i.e. supplementary to the interior angle) has a measure of  {\tfrac {360}{n}} degrees, with the sum of the exterior angles equal to 360 degrees or 2π radians or one full turn.

Regular star polygons

A non-convex regular polygon is a regular star polygon. The most common example is the pentagram, which has the same vertices as a pentagon, but connects alternating vertices.

For an n-sided star polygon, the Schläfli symbol is modified to indicate the density or “starriness” m of the polygon, as {n/m}. If m is 2, for example, then every second point is joined. If m is 3, then every third point is joined. The boundary of the polygon winds around the center m times.

The (non-degenerate) regular stars of up to 12 sides are:

m and n must be coprime, or the figure will degenerate.

The degenerate regular stars of up to 12 sides are:

  • Square – {4/2}
  • Hexagons – {6/2}, {6/3}
  • Octagons – {8/2}, {8/4}
  • Enneagon – {9/3}
  • Decagons – {10/2}, {10/4} and {10/5}
  • Dodecagons – {12/2}, {12/3}, {12/4} and {12/6}
Two interpretations of {6/2}
Grünbaum
{6/2} or 2{3}[11]		 Coxeter
2{3} or {6}[2{3}]{6}
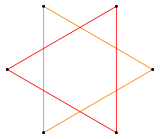Doubly wound hexagon.png Regular star figure 2(3,1).svg
Doubly-wound hexagon Hexagram as a compound
of two triangles

Depending on the precise derivation of the Schläfli symbol, opinions differ as to the nature of the degenerate figure. For example, {6/2} may be treated in either of two ways:

  • For much of the 20th century (see for example Coxeter (1948)), we have commonly taken the /2 to indicate joining each vertex of a convex {6} to its near neighbors two steps away, to obtain the regular compound of two triangles, or hexagram.
Coxeter clarifies this regular compound with a notation {kp}[k{p}]{kp} for the compound {p/k}, so the hexagram is represented as {6}[2{3}]{6}.[12] More compactly Coxeter also writes 2{n/2}, like 2{3} for a hexagram as compound as alternations of regular even-sided polygons, with italics on the leading factor to differentiate it from the coinciding interpretation.[13]
  • Many modern geometers, such as Grünbaum (2003),[11] regard this as incorrect. They take the /2 to indicate moving two places around the {6} at each step, obtaining a “double-wound” triangle that has two vertices superimposed at each corner point and two edges along each line segment. Not only does this fit in better with modern theories of abstract polytopes, but it also more closely copies the way in which Poinsot (1809) created his star polygons – by taking a single length of wire and bending it at successive points through the same angle until the figure closed.

 

，豈非鮮有驚豔，邯鄲學步的耶★☆故而將用從上到下  Top-Down 論此小海龜繪圖幾何學的乎！！