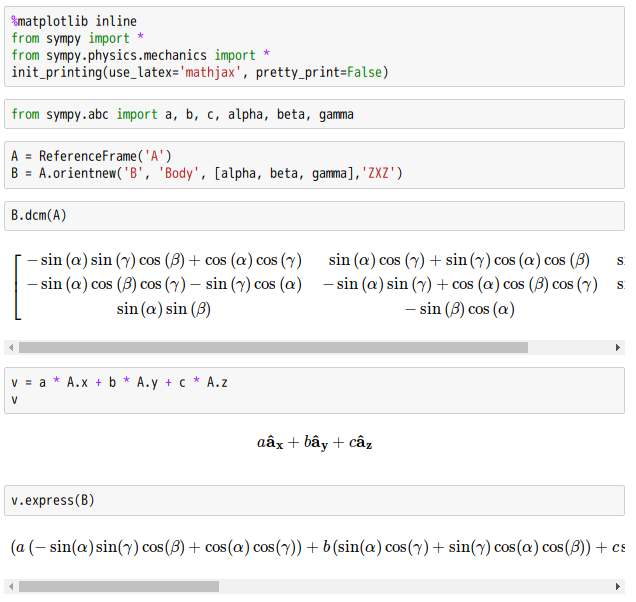
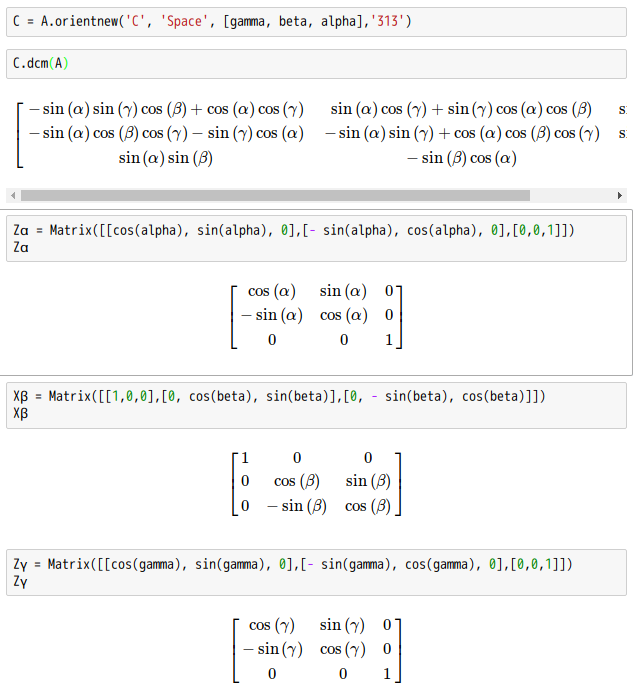
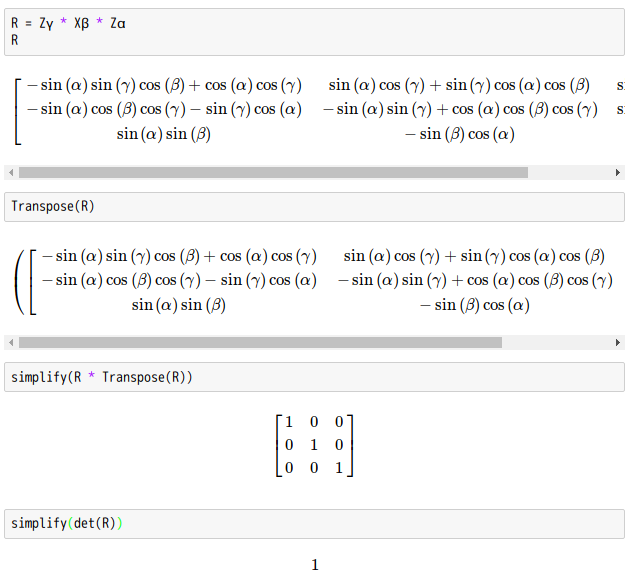
要是我們不熟悉一個程式庫使用的術語︰
ReferenceFrame
- class
sympy.physics.vector.frame.ReferenceFrame(name, indices=None, latexs=None, variables=None) - A reference frame in classical mechanics.
ReferenceFrame is a class used to represent a reference frame in classical mechanics. It has a standard basis of three unit vectors in the frame’s x, y, and z directions.
It also can have a rotation relative to a parent frame; this rotation is defined by a direction cosine matrix relating this frame’s basis vectors to the parent frame’s basis vectors. It can also have an angular velocity vector, defined in another frame.
……
orient(parent, rot_type, amounts, rot_order=”)
Defines the orientation of this frame relative to a parent frame.
| Parameters: |
parent : ReferenceFrame
rot_type : str
amounts : list OR value
rot_order : str
|
|---|
單靠簡單的例子,通常無法弄清用法也︰
Examples
>>> from sympy.physics.vector import ReferenceFrame, Vector
>>> from sympy import symbols, eye, ImmutableMatrix
>>> q0, q1, q2, q3 = symbols('q0 q1 q2 q3')
>>> N = ReferenceFrame('N')
>>> B = ReferenceFrame('B')
Now we have a choice of how to implement the orientation. First is Body. Body orientation takes this reference frame through three successive simple rotations. Acceptable rotation orders are of length 3, expressed in XYZ or 123, and cannot have a rotation about about an axis twice in a row.
>>> B.orient(N, 'Body', [q1, q2, q3], '123') >>> B.orient(N, 'Body', [q1, q2, 0], 'ZXZ') >>> B.orient(N, 'Body', [0, 0, 0], 'XYX')
Next is Space. Space is like Body, but the rotations are applied in the opposite order.
>>> B.orient(N, 'Space', [q1, q2, q3], '312')
Next is Quaternion. This orients the new ReferenceFrame with Quaternions, defined as a finite rotation about lambda, a unit vector, by some amount theta. This orientation is described by four parameters: q0 = cos(theta/2) q1 = lambda_x sin(theta/2) q2 = lambda_y sin(theta/2) q3 = lambda_z sin(theta/2) Quaternion does not take in a rotation order.
>>> B.orient(N, 'Quaternion', [q0, q1, q2, q3])
Next is Axis. This is a rotation about an arbitrary, non-time-varying axis by some angle. The axis is supplied as a Vector. This is how simple rotations are defined.
>>> B.orient(N, 'Axis', [q1, N.x + 2 * N.y])
Last is DCM (Direction Cosine Matrix). This is a rotation matrix given manually.
>>> B.orient(N, 'DCM', eye(3)) >>> B.orient(N, 'DCM', ImmutableMatrix([[0, 1, 0], [0, 0, -1], [-1, 0, 0]]))
比方說『Body』和『Space』都可指『歐拉角』,讀一讀維基百科詞條或能明白所指是什麼︰
歐拉角
萊昂哈德·歐拉用歐拉角來描述剛體在三維歐幾里得空間的取向。對於任何參考系,一個剛體的取向,是依照順序,從這參考系,做三個歐拉角的旋轉而設定的。所以,剛體的取向可以用三個基本旋轉矩陣來決定。換句話說,任何關於剛體旋轉的旋轉矩陣是由三個基本旋轉矩陣複合而成的。
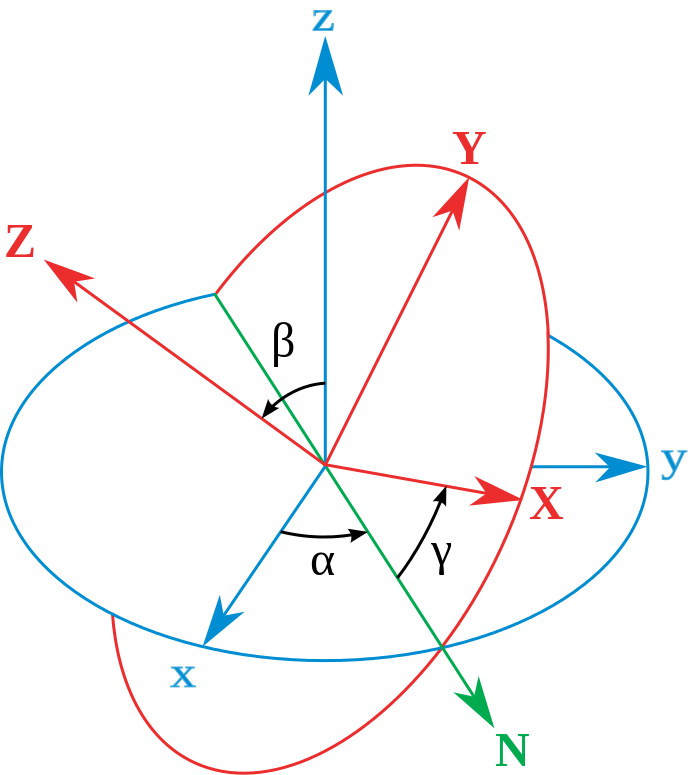
三個歐拉角: (α, β, γ)。藍色的軸是 xyz-軸,紅色的軸是 XYZ-坐標軸 。綠色的線是交點線 (N)。
靜態的定義
對於在三維空間裏的一個參考系,任何坐標系的取向,都可以用三個歐拉角來表現。參考系又稱為實驗室參考系,是靜止不動的。而坐標系則固定於剛體,隨著剛體的旋轉而旋轉。
參閲右圖。設定xyz-軸為參考系的參考軸。稱 xy-平面與 XY-平面的相交為交點線,用英文字母(N)代表。 zxz 順規的歐拉角可以靜態地這樣定義:
- α 是x-軸與交點線的夾角,
- β 是z-軸與Z-軸的夾角,
- γ 是交點線與X-軸的夾角。
很可惜地,對於夾角的順序和標記,夾角的兩個軸的指定,並沒有任何常規。科學家對此從未達成共識。每當用到歐拉角時,我們必須明確的表示出夾角的順序,指定其參考軸。
實際上,有許多方法可以設定兩個坐標系的相對取向。歐拉角方法只是其中的一種。此外,不同的作者會用不同組合的歐拉角來描述,或用不同的名字表示同樣的歐拉角。因此,使用歐拉角前,必須先做好明確的定義。
角值範圍
- α、γ 值分別從 0 至 2π 弧度。
- β 值從 0 至 π 弧度。
對應於每一個取向,設定的一組歐拉角都是獨特唯一的;除了某些例外:
- 兩組歐拉角的 α ,一個是0,一個是 2π,而 β 與 γ 分別相等,則此兩組歐拉角都描述同樣的取向。
- 兩組歐拉角的 γ ,一個是 0,一個是 2π,而 α 與 β 分別相等,則此兩組歐拉角都描述同樣的取向。
旋轉矩陣
前面提到,設定剛體取向的旋轉矩陣 ![]() 是由三個基本旋轉矩陣合成的:
是由三個基本旋轉矩陣合成的:
![Rendered by QuickLaTeX.com \displaystyle [\mathbf {R} ]={\begin{bmatrix}\cos \gamma &\sin \gamma &0\\-\sin \gamma &\cos \gamma &0\\0&0&1\end{bmatrix}}{\begin{bmatrix}1&0&0\\0&\cos \beta &\sin \beta \\0&-\sin \beta &\cos \beta \end{bmatrix}}{\begin{bmatrix}\cos \alpha &\sin \alpha &0\\-\sin \alpha &\cos \alpha &0\\0&0&1\end{bmatrix}}](http://www.freesandal.org/wp-content/ql-cache/quicklatex.com-f9b05d1323eada3a1326bcdfb0d8ed30_l3.png)
- 從左到右依次代表繞著z軸的旋轉、繞著交點線的旋轉、繞著Z軸的旋轉。
經過一番運算,
![Rendered by QuickLaTeX.com \displaystyle [\mathbf {R} ]={\begin{bmatrix}\cos \alpha \cos \gamma -\cos \beta \sin \alpha \sin \gamma &\sin \alpha \cos \gamma +\cos \beta \cos \alpha \sin \gamma &\sin \beta \sin \gamma \\-\cos \alpha \sin \gamma -\cos \beta \sin \alpha \cos \gamma &-\sin \alpha \sin \gamma +\cos \beta \cos \alpha \cos \gamma &\sin \beta \cos \gamma \\\sin \beta \sin \alpha &-\sin \beta \cos \alpha &\cos \beta \end{bmatrix}}](http://www.freesandal.org/wp-content/ql-cache/quicklatex.com-1aea915f7324ab40e84bbfdf9cfcda66_l3.png)
![Rendered by QuickLaTeX.com \displaystyle [\mathbf {R} ]](http://www.freesandal.org/wp-content/ql-cache/quicklatex.com-3409ff25d6f5cdd4fa1befd19bd3df62_l3.png) 的逆矩陣是:
的逆矩陣是:![Rendered by QuickLaTeX.com \displaystyle [\mathbf {R} ]^{-1}={\begin{bmatrix}\cos \alpha \cos \gamma -\cos \beta \sin \alpha \sin \gamma &-\cos \alpha \sin \gamma -\cos \beta \sin \alpha \cos \gamma &\sin \beta \sin \alpha \\\sin \alpha \cos \gamma +\cos \beta \cos \alpha \sin \gamma &-\sin \alpha \sin \gamma +\cos \beta \cos \alpha \cos \gamma &-\sin \beta \cos \alpha \\\sin \beta \sin \gamma &\sin \beta \cos \gamma &\cos \beta \end{bmatrix}}](http://www.freesandal.org/wp-content/ql-cache/quicklatex.com-17072c040bc89d6b6f9ac81cca10c3cb_l3.png)
別種順序
在古典力學裏,時常用 zxz 順規來設定歐拉角;照著第二個轉動軸的軸名,簡稱為 x 順規。另外,還有別種歐拉角組。合法的歐拉角組中,唯一的限制是,任何兩個連續的旋轉,必須繞著不同的轉動軸旋轉。因此,一共有12種順規。例如, y 順規,第二個轉動軸是 y-軸,時常用在量子力學、核子物理學、粒子物理學。另外,還有一種順規, xyz 順規,是用在航空航天工程學;參閱泰特-布萊恩角。
動態的定義
我們也可以給予歐拉角兩種不同的動態定義。一種是繞著固定於剛體的坐標軸的三個旋轉的複合;另外一種是繞著實驗室參考軸的三個旋轉的複合。用動態的定義,我們能更了解,歐拉角在物理上的含義與應用。特別注意,以下的描述, XYZ 坐標軸是旋轉的剛體坐標軸;而 xyz 坐標軸是靜止不動的實驗室參考軸。
- A) 繞著 XYZ 坐標軸旋轉:最初,兩個坐標系統 xyz 與 XYZ 的坐標軸都是重疊著的。開始先繞著Z-軸旋轉 α 角值。然後,繞著 X-軸旋轉 β 角值。最後,繞著 Z-軸作角值 γ 的旋轉。
- B) 繞著 xyz 坐標軸旋轉:最初,兩個坐標系統 xyz 與 XYZ 的坐標軸都是重疊著的。開始先繞著z-軸旋轉 γ 角值。然後,繞著 x-軸旋轉 β 角值。最後,繞著 z-軸作角值 α 的旋轉。
參閱歐拉角圖,定義A與靜態定義的相等,這可以直接用幾何製圖方法來核對。
定義A與定義B的相等可以用旋轉矩陣來證明:
思考任何一點 ![]() ,在 xy z與 XYZ坐標系統的坐標分別為
,在 xy z與 XYZ坐標系統的坐標分別為 ![]() 與
與 ![]() 。定義角算符
。定義角算符 ![]() 為繞著Z-軸旋轉 α 角值。那麼,定義 A 可以表述如下:
為繞著Z-軸旋轉 α 角值。那麼,定義 A 可以表述如下:
![]() 。
。
用旋轉矩陣表示,
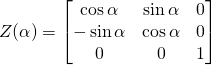 ,
,
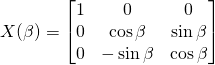 ,
,
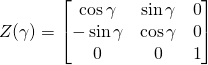 。
。
思考任何一點 ![]() ,在 xyz 與 XYZ 坐標系統的坐標分別為
,在 xyz 與 XYZ 坐標系統的坐標分別為 ![]() 與
與 ![]() 。定義角算符
。定義角算符 ![]() 為繞著z-軸旋轉 α 角值。則定義 B 可以表述如下:
為繞著z-軸旋轉 α 角值。則定義 B 可以表述如下:
![]() 。
。
用旋轉矩陣表示,
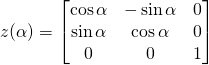 ,
,
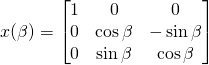 ,
,
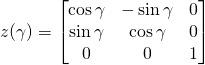 。
。
假設, ![]() 那麼,
那麼,
![]() 。
。
乘以逆算符,
![]() 。
。
但是,從旋轉矩陣可以觀察出,
![]() ,
,
![]() ,
,
![]() 。
。
所以,
![]() ,
,
![]() 。
。
定義 A 與定義 B 是相等的。
然而最好確定其指呦!!??