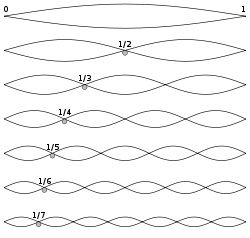
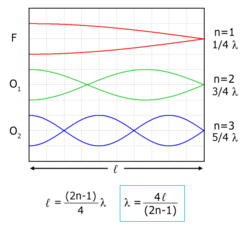
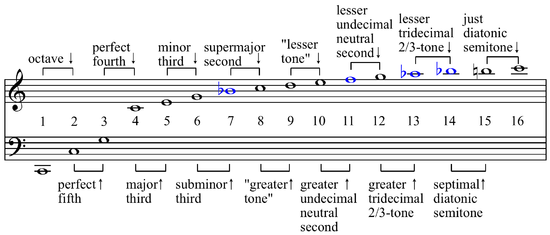
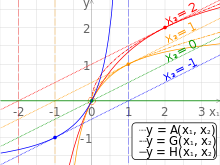
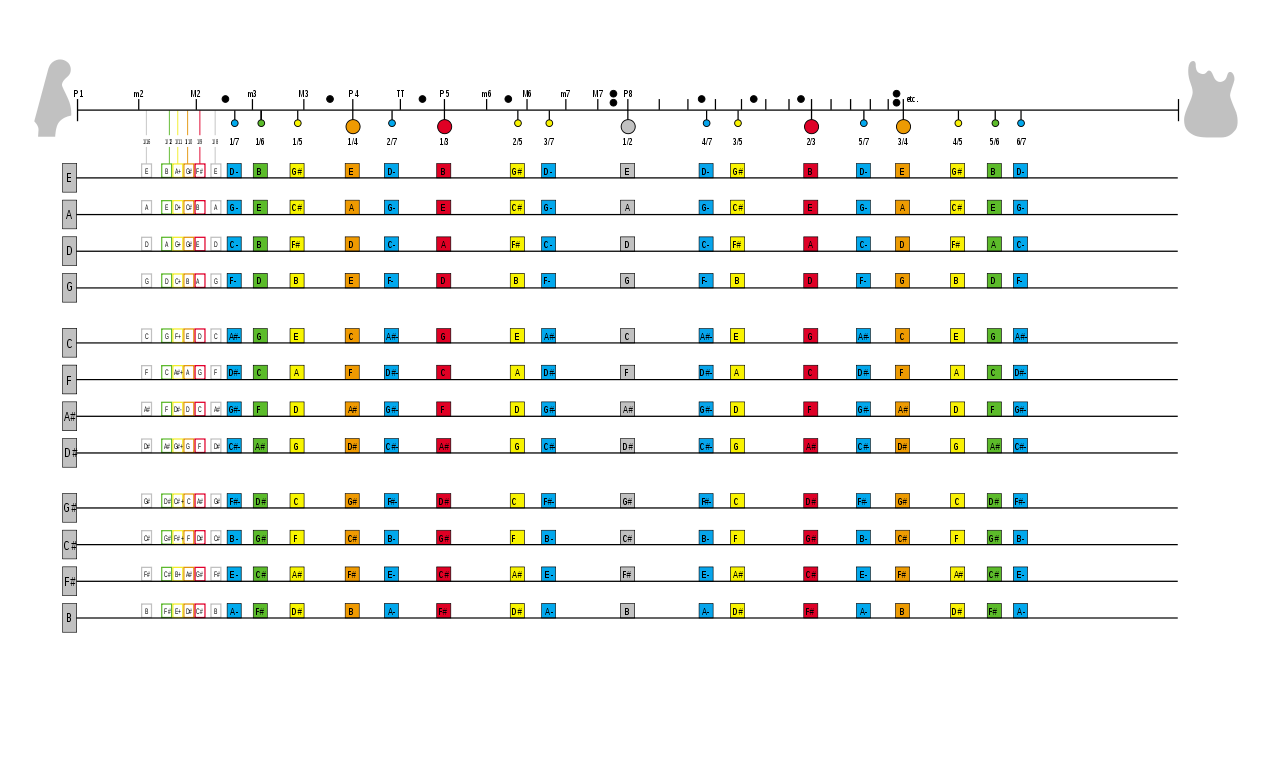
在《【Sonic π】聲波之傳播原理︰原理篇《四下》》一文中我們談到了『駐波』的形成,之後又說明了『樂器』製造通常需要『共振腔』 的放大。事實上『調和序列』 ![]() ,與『調和級數』
,與『調和級數』 ![]() 的『調和』之名源於『樂理』中的『泛音』 overtone 和『泛音列』 harmonic series。一首『樂曲』從『數學』上講,就是一個個『音符』構成的頻率序列,在『時序』上『和諧』的展開,因此才有人說︰『音樂』是有聲的『數學』,『數學』是無聲的『音樂』的啊!我們如果自『遞迴關係式』所比之擬之『相空間』的『符號動力學』來看,或許它該說是『物理』中的『音符動力學』的吧!
的『調和』之名源於『樂理』中的『泛音』 overtone 和『泛音列』 harmonic series。一首『樂曲』從『數學』上講,就是一個個『音符』構成的頻率序列,在『時序』上『和諧』的展開,因此才有人說︰『音樂』是有聲的『數學』,『數學』是無聲的『音樂』的啊!我們如果自『遞迴關係式』所比之擬之『相空間』的『符號動力學』來看,或許它該說是『物理』中的『音符動力學』的吧!
即使由『調和平均數』一詞來說,假使 ![]() 是一個『調和序列』的第
是一個『調和序列』的第 ![]() 項,那麼任意兩項的『調和平均數』
項,那麼任意兩項的『調和平均數』 ![]() 就是
就是 ![]() ,所以
,所以 ![]() 。於是『調和序列』中任意連續的三個數
。於是『調和序列』中任意連續的三個數 ![]() 『全部』都構成了『調和平均數』之『關係』
『全部』都構成了『調和平均數』之『關係』 ![]() 。因此這就是『為什麼』那個『調和序列』會被稱之為『調和』的了。現實裡,大概也只有大自然中,那不期而遇的『山光水影』之『漸層』 的『美』,方能夠與之『匹配』的吧!!
。因此這就是『為什麼』那個『調和序列』會被稱之為『調和』的了。現實裡,大概也只有大自然中,那不期而遇的『山光水影』之『漸層』 的『美』,方能夠與之『匹配』的吧!!
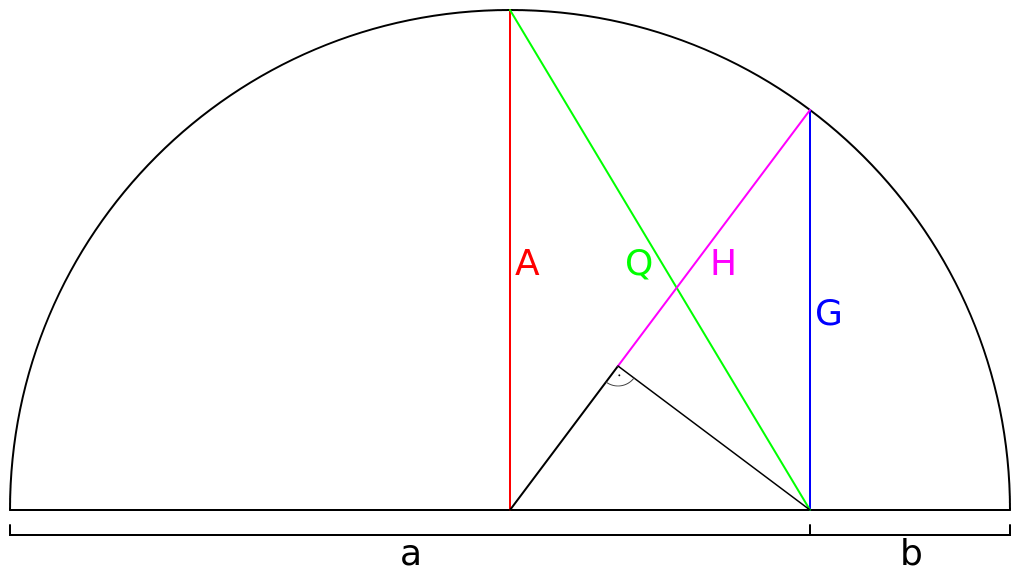
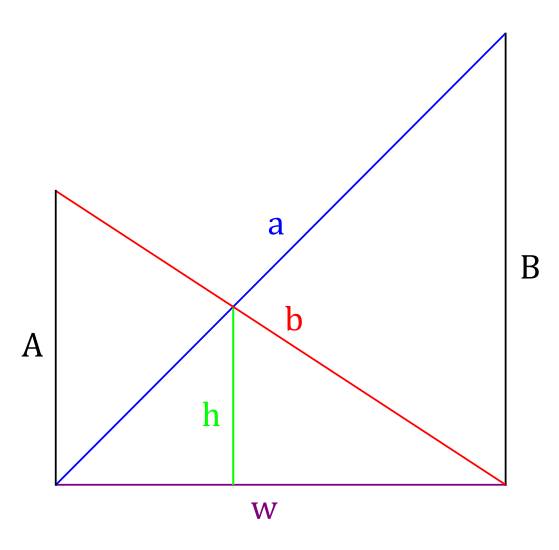
幾何上講,![]() 兩正數的算術平均值是
兩正數的算術平均值是 ![]() ,幾何平均量是
,幾何平均量是 ![]() ,搭配上調和平均數
,搭配上調和平均數 ![]() 滿足
滿足 ![]() 。如果再添上『平方平均數』
。如果再添上『平方平均數』 ![]() ,彼此間擁有
,彼此間擁有 ![]() 的關係。
的關係。
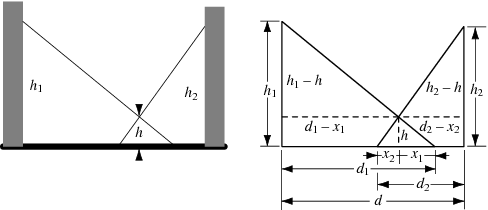
作者不知從何時起網路上開始流傳了一個『交叉梯子之問題』 Crossed ladders problem,根據『 Wolfram‧mathworld』的索引,它來自於
Gardner, M. Mathematical Circus: More Puzzles, Games, Paradoxes and Other Mathematical Entertainments from Scientific American. New York: Knopf, pp. 62-64, 1979.
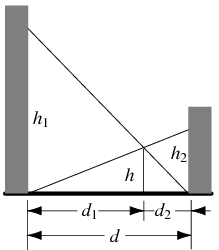
這本書。為什麼它又被稱之為『迷惑‧難題』 puzzle 的呢?假使你知道『巷子』中兩根斜擺的『梯子』的長度是 ![]() ,你也知道它的『交叉點』距地的『高度』是
,你也知道它的『交叉點』距地的『高度』是 ![]() ,那麼你能不能算出『巷寬』
,那麼你能不能算出『巷寬』 ![]() 的呢?
的呢?
由於 ![]() 和
和 ![]() ,可以得到
,可以得到 ![]() 與
與 ![]() 。然而
。然而 ![]() ,化簡後得到
,化簡後得到 ![]() ,這三者竟然滿足這個『不預期』之『關係式』,而且不見
,這三者竟然滿足這個『不預期』之『關係式』,而且不見 ![]() 的蹤影了。假設
的蹤影了。假設 ![]() 的梯子長
的梯子長 ![]() ,
,![]() 的梯子長
的梯子長 ![]() ,由『畢氏定理』可以得到
,由『畢氏定理』可以得到 ![]() 與
與 ![]() ,所以
,所以 ![]() ,因此
,因此 ![]()
![]() ,由於
,由於 ![]() ,因此
,因此 ![]() ,將之代入上式得到
,將之代入上式得到
![]()
。如果我們仔細考察下面的方程式
![]()
,『左邊項』為『已知量』,『右邊項』是『未知數』 ![]() 的『方程式』。假設
的『方程式』。假設 ![]() ,如果我們定義
,如果我們定義
![]() ,
,![]()
, 可以將之化簡為
![]()
,總是不見『巷寬』 ![]() 的『蹤影』,所以方說令人『迷惑』的啊!竟然得要『求解』四次方程式,因此才是個『難題』的吧!更不要講它還能夠有全『整數解』,舉例來說,
的『蹤影』,所以方說令人『迷惑』的啊!竟然得要『求解』四次方程式,因此才是個『難題』的吧!更不要講它還能夠有全『整數解』,舉例來說,![]() ,果然是奇也怪哉!!
,果然是奇也怪哉!!
假使我們已經解得了 ![]() ,那麼要怎們求出『巷寬』
,那麼要怎們求出『巷寬』![]() 的呢?我們還得解下面的方程式?? 假設
的呢?我們還得解下面的方程式?? 假設 ![]()
![]()
![]()
,用二次方程式的『公式解』可以得到
![]()
![]()
再由,![]() ,因此
,因此 ![]() ,因為
,因為 ![]() ,所以那個久違的『巷寬』就是
,所以那個久違的『巷寬』就是 ![]() !!
!!
有人問為什麼要『假設』 ![]() 的呢?由於那個『方程式』對於
的呢?由於那個『方程式』對於 ![]() 與
與 ![]() 來講是『對稱的』,所以除非這兩者『相等』,否則『假設』
來講是『對稱的』,所以除非這兩者『相等』,否則『假設』 ![]() 只是方便論述而已,畢竟『根號』內之數在此該是正的啊!再者當
只是方便論述而已,畢竟『根號』內之數在此該是正的啊!再者當 ![]() 時,就有
時,就有 ![]() 的關係存在,就可以直接求得
的關係存在,就可以直接求得 ![]() 的了!如此根本不需要解那個四次方程式的吧!!
的了!如此根本不需要解那個四次方程式的吧!!
如果從『直覺上』來講,假使當 ![]() ,此時
,此時 ![]() ,那麼我們能夠求得
,那麼我們能夠求得 ![]() 之『極限值』的嗎?因為這時
之『極限值』的嗎?因為這時 ![]() ,因此
,因此![]() ,所以那個四次方程式就變成了
,所以那個四次方程式就變成了 ![]() ,它有四個解
,它有四個解 ![]() ,於是
,於是 ![]() ,由於
,由於 ![]() ,故得
,故得 ![]() 。
。
許多看似『無關』的『知識』片段,往往具有『內在』的『肌理』關係,就此觀之,『學習』一事常在『發現』這個『關係』,以及『貫通』現象之間內在的『聯繫』的啊!!