具體數學:計算機科學之基石
An ant starts to crawl along a taut rubber rope 1 km long at a speed of 1 cm per second (relative to the rubber it is crawling on). At the same time, the rope starts to stretch uniformly by 1 km per second, so that after 1 second it is 2 km long, after 2 seconds it is 3 km long, etc. Will the ant ever reach the end of the rope?
在『具體數學』這本書中提到了另一個『違反直覺』的例子 ── 橡膠繩上的螞蟻 ──,一隻螞蟻以每秒鐘一公分的速度,在一根長一公里拉緊了的橡膠繩上爬行【螞蟻的爬行速度相對橡膠繩】,就在螞蟻爬行的同時,橡膠繩也以每秒一公里的速度伸長,也就是說一秒後,它有兩公里長,兩秒後有三公里長等等。試問螞蟻果真到的了繩子之另一端的嗎?
假設 ![]() 時刻時,螞蟻在
時刻時,螞蟻在 ![]() 的『位置』,以
的『位置』,以 ![]() 的速度朝另一端爬行,同時橡膠繩用
的速度朝另一端爬行,同時橡膠繩用 ![]() 的速度同向均勻伸長,因此橡膠繩上的某點
的速度同向均勻伸長,因此橡膠繩上的某點 ![]() 的伸長速度將是
的伸長速度將是 ![]() ,此處
,此處 ![]() 就是橡膠繩的『原長』,由於起點是『固定』不動的,因此繩上各點的速度與『端點的速度』
就是橡膠繩的『原長』,由於起點是『固定』不動的,因此繩上各點的速度與『端點的速度』 ![]() 成比例,於是對於一個靜止的觀察者而言,螞蟻的速度將是
成比例,於是對於一個靜止的觀察者而言,螞蟻的速度將是
![]()
。如果我們設想要是橡膠繩並不與時伸展,那麼這隻螞蟻是一定到的了彼端,假使一個相對於繩子靜止的觀察者將看到什麼現象的呢?或許他將用 ![]() 來描述這隻螞蟻的行進的吧! 它從
來描述這隻螞蟻的行進的吧! 它從 ![]() 開始爬行,它將會在
開始爬行,它將會在 ![]() 時刻到達了另一端。由於
時刻到達了另一端。由於
![]()
![]()
![]()
![]() ,因此我們就可以得到
,因此我們就可以得到
![]()
此處 ![]() 積分常數。從
積分常數。從 ![]() ,可以得到
,可以得到 ![]() ,所以
,所以 ![]() 。再從
。再從 ![]() ,就得到了
,就得到了 ![]() 。
。
假使將 ![]() 代入後,求得
代入後,求得 ![]() ,這隻小螞蟻果真到的了彼端,雖然它得經過千千萬萬個三千大劫的吧!!
,這隻小螞蟻果真到的了彼端,雖然它得經過千千萬萬個三千大劫的吧!!
那麼為什麼 ︰某點 ![]() 的伸長速度會是
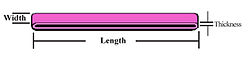
的伸長速度會是 ![]() 的呢?假使考慮一根『有刻度』
的呢?假使考慮一根『有刻度』 ![]() 的尺,它的一端固定,另一端向外延伸,這樣每個『刻度點』也都相對的向外伸長
的尺,它的一端固定,另一端向外延伸,這樣每個『刻度點』也都相對的向外伸長 ![]() ,於是『固定端』
,於是『固定端』 ![]() ,『第一個刻度』在
,『第一個刻度』在 ![]() 的位置,『第二個刻度』在
的位置,『第二個刻度』在 ![]() 的位置,這樣『第
的位置,這樣『第 ![]() 個刻度』將在
個刻度』將在 ![]() 的位置。假設『橡膠繩』的『彈性』是『均勻』的,這樣所有的
的位置。假設『橡膠繩』的『彈性』是『均勻』的,這樣所有的 ![]() 都相等,因此
都相等,因此 ![]() ,如此當『另一端』用『定速』
,如此當『另一端』用『定速』 ![]() 移動時,此時
移動時,此時 ![]() ,於是『第
,於是『第 ![]() 個刻度』就用
個刻度』就用 ![]() 的速度在移動的啊!
的速度在移動的啊!
過去有人曾經想像過一種情況︰如果說宇宙中的一切,在夜間會突然的『變大』或者『縮小』,那麼我們能夠『發現』的嗎?假使從『量測』的觀點來看,如果度量用的『尺』 ![]() 隨著時間改變,『被度量事物』的『大小』
隨著時間改變,『被度量事物』的『大小』 ![]() 也『協同』的跟隨著變化
也『協同』的跟隨著變化 ![]() ,這樣在那個『宇宙』 裡面
,這樣在那個『宇宙』 裡面 ![]() ,也就是講『測量』沒有辦法『知道』到底『有沒有』發生過這件事的啊!!然而這卻更進一步引發了『自然定律』到底是否會在『度量單位』的改變下,而有所不同的呢??
,也就是講『測量』沒有辦法『知道』到底『有沒有』發生過這件事的啊!!然而這卻更進一步引發了『自然定律』到底是否會在『度量單位』的改變下,而有所不同的呢??
之前在《亞里斯多德之輪!!》一文中,我們談到了『伽利略』的『無窮觀』。一六三八年,伽利略在『兩種新科學』 Two New Sciences 一書中,提出了『平方立方定律』。假使一個『物體』等比例放大 ![]() 倍,那麼它的『面積』將放大
倍,那麼它的『面積』將放大 ![]() 倍,而且它的『體積』將放大
倍,而且它的『體積』將放大 ![]() 倍。這難到又有什麼奇怪的嗎?
倍。這難到又有什麼奇怪的嗎?
如果思考在大地上『重力』作用下『生物』之『承受力』的問題,當可以明白『壓力』是『單位面積』所負載的『重量』。如此將之『等比例放大』後,這個『壓力』 ![]() ,將正比於『放大倍率』
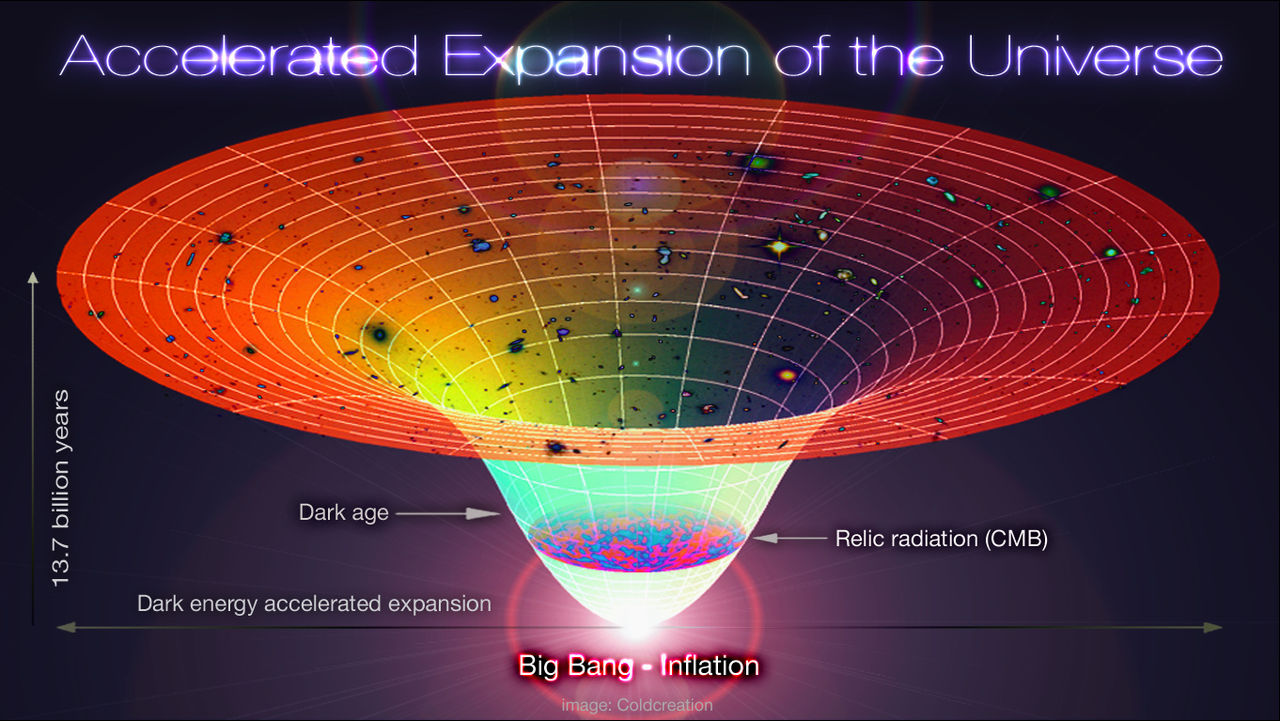
,將正比於『放大倍率』 ![]() ,所以說一棵樹,並不能夠一直向上生長,一隻螞蟻也很難變大數萬倍而不受影響的啊!如此講來天文學上所說的『宇宙膨漲』應該是有『現象』依據的吧!然而既然已經說是『宇宙』的了,它又該往『哪裡膨漲』的呢??或許《科赫傳說!!》裡的『雪花維度』是一個『起始點』的吧!!
,所以說一棵樹,並不能夠一直向上生長,一隻螞蟻也很難變大數萬倍而不受影響的啊!如此講來天文學上所說的『宇宙膨漲』應該是有『現象』依據的吧!然而既然已經說是『宇宙』的了,它又該往『哪裡膨漲』的呢??或許《科赫傳說!!》裡的『雪花維度』是一個『起始點』的吧!!
從數學的觀點來看,![]() 是一個所謂的『一階微分方程式』的『積分因子』,這可以讓我們求得『答案』,祇不過它的『意義』又是什麼的呢?就物理上來講,它的意思是說,假使將
是一個所謂的『一階微分方程式』的『積分因子』,這可以讓我們求得『答案』,祇不過它的『意義』又是什麼的呢?就物理上來講,它的意思是說,假使將 ![]() 當作一根『單位尺』。雖然說我們看來在『那個宇宙』裡, 這個『尺度』隨著時 間變化,這也不過就是那裡『時時刻刻』的『測量值』的吧。如果說一隻小螞蟻自『開始』就永往『終點』行進,假使它不會『退轉』,那麼它到底能不能夠『抵達』終點的啊?設想一旦它於某個
當作一根『單位尺』。雖然說我們看來在『那個宇宙』裡, 這個『尺度』隨著時 間變化,這也不過就是那裡『時時刻刻』的『測量值』的吧。如果說一隻小螞蟻自『開始』就永往『終點』行進,假使它不會『退轉』,那麼它到底能不能夠『抵達』終點的啊?設想一旦它於某個 ![]() 時刻到達了『終點』,那一根尺的『終點』與這一隻小螞蟻之最後『位置』也就重合的了。所以就一個『慣性座標系』靜止的觀察者來講﹐這個發生的『事件』之『距離』也是『相同的』啊!然而就那個『繩上的觀察者』來講,這隻螞蟻不過就是走過了『一單位』的距離罷了!!
時刻到達了『終點』,那一根尺的『終點』與這一隻小螞蟻之最後『位置』也就重合的了。所以就一個『慣性座標系』靜止的觀察者來講﹐這個發生的『事件』之『距離』也是『相同的』啊!然而就那個『繩上的觀察者』來講,這隻螞蟻不過就是走過了『一單位』的距離罷了!!