無窮可知不可極︰
一九六零年,德國數學家『亞伯拉罕‧魯濱遜』 Abraham Robinson 將『萊布尼茲』的微分直觀落實。 用嚴謹的方法來定義和運算實數的『無窮小』與『無限大』,這就是數學史上著名的『非標準微積分』Non-standard calculus ,可說是『非標準分析』non-standard analysis 之父。
就像『複數』 ![]() 是『實數系』
是『實數系』 ![]() 的『擴張』一樣,他將『實數系』增入了『無窮小』 infinitesimals 元素
的『擴張』一樣,他將『實數系』增入了『無窮小』 infinitesimals 元素 ![]() ,魯濱遜創造出『超實數』 hyperreals
,魯濱遜創造出『超實數』 hyperreals ![]() ,形成了『超實數系』
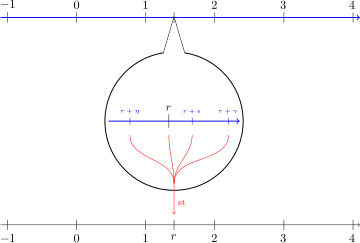
,形成了『超實數系』 ![]() 。那這個『無窮小』是什麼樣的『數』呢?對於『正無窮小』來說,任何給定的『正數』都比要它大,就『負無窮小』來講,它大於任何給定的『負數』。 『零』也就自然的被看成『實數系』裡的『無窮小』的了。假使我們說兩個超實數
。那這個『無窮小』是什麼樣的『數』呢?對於『正無窮小』來說,任何給定的『正數』都比要它大,就『負無窮小』來講,它大於任何給定的『負數』。 『零』也就自然的被看成『實數系』裡的『無窮小』的了。假使我們說兩個超實數 ![]() 是『無限的鄰近』 indefinitly close,記作
是『無限的鄰近』 indefinitly close,記作 ![]() 是指
是指 ![]() 是個『無窮小』量。在這個觀點下,『無窮小』量不滿足『實數』的『阿基米德性質』。也就是說,對於任意給定的
是個『無窮小』量。在這個觀點下,『無窮小』量不滿足『實數』的『阿基米德性質』。也就是說,對於任意給定的 ![]() 來講,
來講, ![]() 為『無窮小』量;而
為『無窮小』量;而 ![]() 是『無限大』量。然而在『系統』與『自然』的『擴張』下,『超實數』的『算術』符合所有一般『代數法則』。
是『無限大』量。然而在『系統』與『自然』的『擴張』下,『超實數』的『算術』符合所有一般『代數法則』。
有人把『超實數』想像成『數原子』,一個環繞著『無窮小』數的『實數』。就像『複數』有『實部』 ![]() 與『虛部』
與『虛部』 ![]() 取值『運算』一樣,『超實數』也有一個取值『運算』叫做『標準部份函數』Standard part function
取值『運算』一樣,『超實數』也有一個取值『運算』叫做『標準部份函數』Standard part function
![]()
![]()
。 如此一個『函數』 ![]() 在
在 ![]() 是『連續的』就可以表示成『如果
是『連續的』就可以表示成『如果 ![]() ,可以得到
,可以得到 ![]() 』。
』。
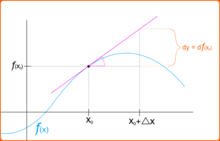
假使 ![]() ,那麼
,那麼 ![]() 的『斜率』就可以這麼計算
的『斜率』就可以這麼計算
![]()
![]()
。 彷彿在用著可以調整『放大倍率』的『顯微鏡』逐步『觀入』 zoom in 一個『函數』,隨著『解析度』的提高,函數之『曲率』逐漸減小,越來越『逼近』一條『直線』── 某點的切線 ── 的啊!!
同樣的『積分』就像是『里程表』的『累計』一樣,可以用
![]()
來表示的呀!!
─── 摘自《【Sonic π】電路學之補充《四》無窮小算術‧中》
道理易解境難抵︰
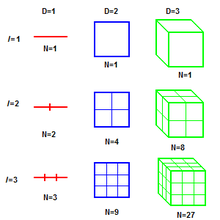
人們『直覺』上都知道,『線』是一維的、『面』是二維的以及『體』是三維的,也許同意『點』是零維的。但是要怎麽定義『維度』 呢?假使設想用一根有刻度的 ![]() 尺,量一條線段,得到
尺,量一條線段,得到 ![]()
![]() ── 單位刻度 ──,如果有另一根
── 單位刻度 ──,如果有另一根 ![]() 的尺,它的單位刻度
的尺,它的單位刻度 ![]() 是
是![]() 尺的
尺的 ![]() 倍,也就是說
倍,也就是說 ![]() ,那用這
,那用這![]() 之尺來量該線段將會得到
之尺來量該線段將會得到 ![]() 。同樣的如果
。同樣的如果 ![]() 尺量一個正方形得到數值
尺量一個正方形得到數值 ![]() ,那用
,那用![]() 之尺來量就會得到數值
之尺來量就會得到數值 ![]() ,這樣那
,這樣那![]() 兩尺的度量之數值比
兩尺的度量之數值比 ![]() 。
。
於是德國數學家費利克斯‧豪斯多夫 Felix Hausdorff 是這樣子定義『維度』![]() 的︰
的︰
![]()
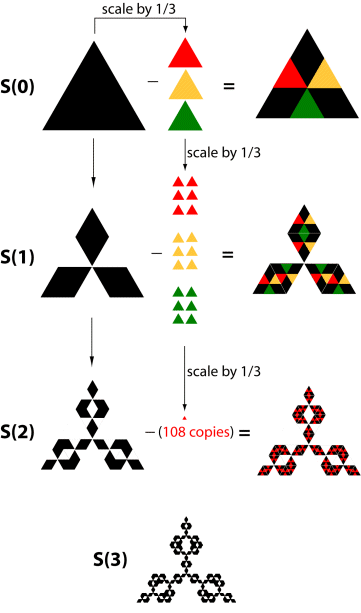
,使它也能適用於『分形』的『分維』。
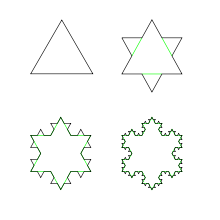
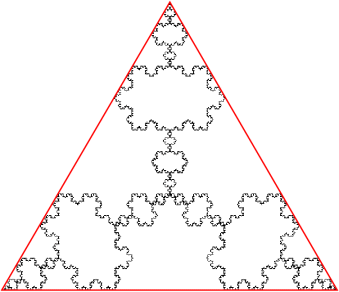
在科赫雪花的建構過程中,從最初 ![]() 的 △,到第
的 △,到第 ![]() 步時︰
步時︰
總邊數︰ ![]()
單一邊長︰ ![]()
總周長︰![]()
圍繞面積︰![]()
因此科赫雪花的分維是
![]()
,它所圍繞的極限面積 ![]() ,那時的總周長
,那時的總周長 ![]() 。
。
─── 摘自《思想實驗!!》
與其撒鹽擬紛紛︰
在那遙遠的銀河裡,有一個科赫王國。那裡的初始之王是一位大智慧者,許下宏願建造永不退轉之國︰本國之土逐年增長,本國之人亦逐年增長,以至無量之無窮無有盡期。不知如此過了幾千千萬萬年,每代之王都謹尊聖諭,於冬至日祭、夏至日祀天上的『雪花之神』, 如是傳到了科赫國王。這個新王想知道聖諭它是真是假?欲明白雪花之神是有是無?於是招集舉國聰明之人有智之士商議調查之法。此舉震驚了全國,大部分的國民 都嚇壞了,說︰這是對神的大不敬;毀壞歷代立下的規矩;不尊重先王的傳統。科赫國王無奈之餘只能禪讓以息民怨,自己踏上了求解之路!他想我要怎麼才能知道 『國土逐年增長』是個事實的呢?於是他首先拜訪了精通『土地丈量』 的人,那丈量人告訴他︰我家無數代以來從事丈量,就我所知的確土地逐年增長。科赫問︰那能知道新增與舊有的差異嗎?丈量人答︰人人舊有的都沒有差異,新土 在之間發生。一番對談後科赫雖心中覺得這事奇怪,但是也無法再多知道些什麼,於是再度踏上旅程。一路上餐風露宿,心理奇怪著為何幼時認得的老人他家還沒到 呢?終於抵達了那稽古老人之住處。問訊之下,老人家身康體泰甚是健談。他聽那老人家抱怨道︰行走都不方便啦!子孫所居山頭相距一代比一代更遠,怕是再過數 年想見都見不著啦!!科赫心頭一震,詳細詢知了老人家的子孫何代幾時是相距多少路程,然後辭別進入山裡沉思不知所蹤。原來科赫自幼喜歡數學,但不知他自己 『身在』雪花中,能否發現『答案』就是『雪花』的呢?知道那個王國要是再經歷無窮世代後,也許會變成『行不得』之國??
後來傳聞科赫國王花了數十年抵達『初始之王』的墓陵,進入墳中關掉了那台年復一年『擴張一步』的『國土製造圖靈機』,並且又再度稱王。這樣想來,或許科赫國王終究找到了『答案』;然而另一個『反科赫王國』大概情況不妙,也許最終凶多吉少,不知是否會有個睿智之王起身自救的嗎??
─── 摘自《科赫傳說!!》
未若柳絮因風起☆★