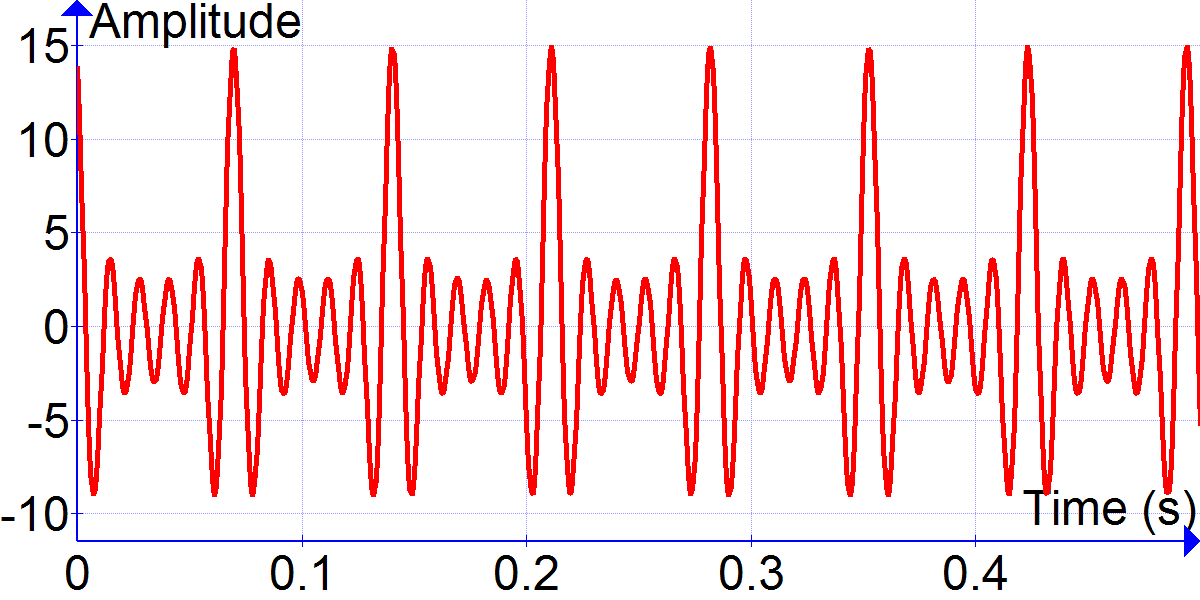
Michael Nielsen 先生之第三章讀來十分有趣,首起
【學習指南】
《論語》‧《學而》
子曰:「學而時習之,不亦說乎?有朋自遠方來,不亦樂乎?人不知而不慍,不亦君子乎?」
孔子說:「經常學習,不也喜悅嗎?遠方來了朋友,不也快樂嗎?得不到理解而不怨恨,不也是君子嗎?」
When a golf player is first learning to play golf, they usually spend most of their time developing a basic swing. Only gradually do they develop other shots, learning to chip, draw and fade the ball, building on and modifying their basic swing. In a similar way, up to now we’ve focused on understanding the backpropagation algorithm. It’s our “basic swing”, the foundation for learning in most work on neural networks. In this chapter I explain a suite of techniques which can be used to improve on our vanilla implementation of backpropagation, and so improve the way our networks learn.
The techniques we’ll develop in this chapter include: a better choice of cost function, known as the cross-entropy cost function; four so-called “regularization” methods (L1 and L2 regularization, dropout, and artificial expansion of the training data), which make our networks better at generalizing beyond the training data; a better method for initializing the weights in the network; and a set of heuristics to help choose good hyper-parameters for the network. I’ll also overview several other techniques in less depth. The discussions are largely independent of one another, and so you may jump ahead if you wish. We’ll also implement many of the techniques in running code, and use them to improve the results obtained on the handwriting classification problem studied in Chapter 1.
Of course, we’re only covering a few of the many, many techniques which have been developed for use in neural nets. The philosophy is that the best entree to the plethora of available techniques is in-depth study of a few of the most important. Mastering those important techniques is not just useful in its own right, but will also deepen your understanding of what problems can arise when you use neural networks. That will leave you well prepared to quickly pick up other techniques, as you need them.
……
止於
【探索地圖】
《論語》‧《堯曰》
堯曰:「咨!爾舜!天之曆數在爾躬。允執其中。四海困窮,天祿永終。」舜亦以命禹。曰:「予小子履,敢用玄牡,敢昭告于皇皇后帝:有罪不敢赦。帝臣不蔽,簡在帝心。朕躬有罪,無以萬方;萬方有罪,罪在朕躬。」周有大賚,善人是富。「雖有周親,不如仁人。百姓有過,在予一人。」謹權量,審法度,修廢官,四方之政行焉。興滅國,繼絕世,舉逸民,天下之民歸心焉。所重:民、食、喪、祭。寬則得眾,信則民任焉,敏則有功,公則說。
堯說:「好啊!你這個舜。天命降臨到你的身上,讓你繼承帝位。如果天下都很窮困,你的帝位也就永遠結束了。」舜也這樣告誡過禹。商湯說:「至高無上的上帝啊,你在人間的兒子–我–謹用黑牛來祭祀您,向您禱告:有罪的人我絕不敢赦免。一切善惡,我都不敢隱瞞,您無所不知,自然心中有數。如果我有罪,請不要牽連天下百姓;如果百姓有罪,罪都應歸結到我身上。」周朝恩賜天下,使好人都富了。武王說:「我雖有至親,都不如有仁人。百姓有錯,在我一人。」孔子說:「謹慎地審查計量,週密地制定法度,建立公正的人事制度,讓國家的法令暢通無阻,復興滅絕的國家,承繼斷絕的世族,提拔埋沒的人才,天下民心都會真心歸服。」掌權者應該重視:人民、糧食、喪葬、祭祀。寬容就能得到人民的擁護,誠信就能使人民的信服。勤敏就能取得功績,公正就能使人民幸福。」
───
On stories in neural networks
Question: How do you approach utilizing and researching machine learning techniques that are supported almost entirely empirically, as opposed to mathematically? Also in what situations have you noticed some of these techniques fail?Answer: You have to realize that our theoretical tools are very weak. Sometimes, we have good mathematical intuitions for why a particular technique should work. Sometimes our intuition ends up being wrong […] The questions become: how well does my method work on this particular problem, and how large is the set of problems on which it works well.
– Question and answer with neural networks researcher Yann LeCun
Once, attending a conference on the foundations of quantum mechanics, I noticed what seemed to me a most curious verbal habit: when talks finished, questions from the audience often began with “I’m very sympathetic to your point of view, but […]“. Quantum foundations was not my usual field, and I noticed this style of questioning because at other scientific conferences I’d rarely or never heard a questioner express their sympathy for the point of view of the speaker. At the time, I thought the prevalence of the question suggested that little genuine progress was being made in quantum foundations, and people were merely spinning their wheels. Later, I realized that assessment was too harsh. The speakers were wrestling with some of the hardest problems human minds have ever confronted. Of course progress was slow! But there was still value in hearing updates on how people were thinking, even if they didn’t always have unarguable new progress to report.
You may have noticed a verbal tic similar to “I’m very sympathetic […]” in the current book. To explain what we’re seeing I’ve often fallen back on saying “Heuristically, […]”, or “Roughly speaking, […]”, following up with a story to explain some phenomenon or other. These stories are plausible, but the empirical evidence I’ve presented has often been pretty thin. If you look through the research literature you’ll see that stories in a similar style appear in many research papers on neural nets, often with thin supporting evidence. What should we think about such stories?
In many parts of science – especially those parts that deal with simple phenomena – it’s possible to obtain very solid, very reliable evidence for quite general hypotheses. But in neural networks there are large numbers of parameters and hyper-parameters, and extremely complex interactions between them. In such extraordinarily complex systems it’s exceedingly difficult to establish reliable general statements. Understanding neural networks in their full generality is a problem that, like quantum foundations, tests the limits of the human mind. Instead, we often make do with evidence for or against a few specific instances of a general statement. As a result those statements sometimes later need to be modified or abandoned, when new evidence comes to light.
One way of viewing this situation is that any heuristic story about neural networks carries with it an implied challenge. For example, consider the statement I quoted earlier, explaining why dropout works* *From ImageNet Classification with Deep Convolutional Neural Networks by Alex Krizhevsky, Ilya Sutskever, and Geoffrey Hinton (2012).: “This technique reduces complex co-adaptations of neurons, since a neuron cannot rely on the presence of particular other neurons. It is, therefore, forced to learn more robust features that are useful in conjunction with many different random subsets of the other neurons.” This is a rich, provocative statement, and one could build a fruitful research program entirely around unpacking the statement, figuring out what in it is true, what is false, what needs variation and refinement. Indeed, there is now a small industry of researchers who are investigating dropout (and many variations), trying to understand how it works, and what its limits are. And so it goes with many of the heuristics we’ve discussed. Each heuristic is not just a (potential) explanation, it’s also a challenge to investigate and understand in more detail.
Of course, there is not time for any single person to investigate all these heuristic explanations in depth. It’s going to take decades (or longer) for the community of neural networks researchers to develop a really powerful, evidence-based theory of how neural networks learn. Does this mean you should reject heuristic explanations as unrigorous, and not sufficiently evidence-based? No! In fact, we need such heuristics to inspire and guide our thinking. It’s like the great age of exploration: the early explorers sometimes explored (and made new discoveries) on the basis of beliefs which were wrong in important ways. Later, those mistakes were corrected as we filled in our knowledge of geography. When you understand something poorly – as the explorers understood geography, and as we understand neural nets today – it’s more important to explore boldly than it is to be rigorously correct in every step of your thinking. And so you should view these stories as a useful guide to how to think about neural nets, while retaining a healthy awareness of the limitations of such stories, and carefully keeping track of just how strong the evidence is for any given line of reasoning. Put another way, we need good stories to help motivate and inspire us, and rigorous in-depth investigation in order to uncover the real facts of the matter.
───
不由得令人想起
Tux 學堂的牆上, 掛著核心 kernel Linus Torvalds 最喜歡的『吃著魚企鵝圖』︰
吃著魚釣魚─── 一個理念、一種方法、一門生活哲學。
強調『理論』與『實務』並重之學習,同修的重要。在這個社會裡,教育是責任,學習是義務!從出生到死亡,所有十方之各族各種企鵝,一體適用!!
還掛著一篇聖諭︰
Tux the Linux penguin
Even people who have never used Linux have probably seen Tux, the penguin mascot of this open-source operating system. Tux was the result of a competition held by the Open Source Software community to find a mascot for Linux. In the forums Linus Torvalds, Finnish creator of Linux, mentioned an encounter he had had with a penguin at Canberra’s National Zoo and Aquarium. Linus claims that he was bitten by a penguin and because of that he was supposedly infected with a disease called “Penguinitis”. This disease caused him to become fixated with penguins.
以及誓言支援拯救袋獾運動的 Tuz 。
這時小企鵝學堂上,嘰嘰喳喳,各地方言七嘴八舌!!萬邦符號亂七八糟,實在難以錄記。原來這『聆老師』以有教無類聞名,通曉萬邦各地語言符號,此刻那些小企鵝們正熱烈議論著『論語讀法』的呢??
有的主張︰半部論語治天下,讀半部。
有的辯證︰就算讀了整部,可是連齊家都不能吔!
有的議論︰是該先誠心、正意、修身的吧!!
有的搞笑︰『始』學而,『終』堯曰!不就兩篇嘛??
…
那你怎個讀法?
哦!唱給你聽︰孔子的中心思想是個仁,……
大概東西人世間只有在『愛情的世界』裡,可能
‧身高不是距離
‧膚色不是問題
‧語言沒有隔閡
‧ …
□不○沒有的吧!!
或即使再忙也要和你喝杯咖啡的好??
有『教改者』義正詞嚴的說︰那種方法我們『試過了』,結果一點也『不管用』︰
老師問︰食色性也,是何意?
學生答︰不吃會死掉,不色無後代!
……
─── 摘自《Tux@rpi ︰ 《學而堯曰》》
但思︰果有人讀書可以『掐頭去尾』『略過中間』的耶??!!













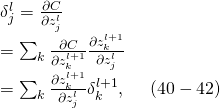
 ,
,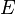 is the squared error,
is the squared error,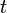 is the target output for a training sample, and
is the target output for a training sample, and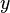 is the actual output of the output neuron.
is the actual output of the output neuron.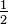 is included to cancel the exponent when differentiating. Later, the expression will be multiplied with an arbitrary learning rate, so that it doesn’t matter if a constant coefficient is introduced now.
is included to cancel the exponent when differentiating. Later, the expression will be multiplied with an arbitrary learning rate, so that it doesn’t matter if a constant coefficient is introduced now. , its output
, its output  is defined as
is defined as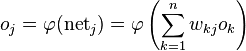 .
.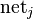 to a neuron is the weighted sum of outputs
to a neuron is the weighted sum of outputs  of previous neurons. If the neuron is in the first layer after the input layer, the
of previous neurons. If the neuron is in the first layer after the input layer, the 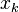 to the network. The number of input units to the neuron is
to the network. The number of input units to the neuron is  . The variable
. The variable  denotes the weight between neurons
denotes the weight between neurons 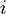 and
and 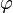 is in general
is in general 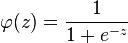


 depends on
depends on 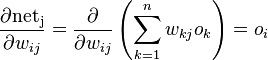 .
. is just
is just  .
.
 and
and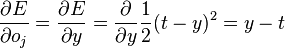
 is less obvious.
is less obvious. receiving input from neuron
receiving input from neuron 

 of the next layer – the one closer to the output neuron – are known.
of the next layer – the one closer to the output neuron – are known.

 . The change in weight, which is added to the old weight, is equal to the product of the learning rate and the gradient, multiplied by
. The change in weight, which is added to the old weight, is equal to the product of the learning rate and the gradient, multiplied by  :
:
 is required in order to update in the direction of a minimum, not a maximum, of the error function.
is required in order to update in the direction of a minimum, not a maximum, of the error function. , which arises if one simply applies the definition of DFT, to
, which arises if one simply applies the definition of DFT, to  , where
, where