伏羲八卦既已義理精當一氣貫通,
將有何說?
然而伏羲乾坤裡,並不見『人』,『人』只是萬物之一而已!故而文王以
,欲立『人』。或可由
《老子》‧《第二十五章》
有物混成,先天地生。
寂兮寥兮,獨立而不改,周行而不殆,可以爲天下母。
吾不知其名,字之曰道。
強爲之名,曰大。大曰逝,逝曰遠,遠曰反。
故道大,天大,地大,王亦大。域中有四大,而王居其一焉。
人法地,地法天,天法道,道法自然。
知其一二。
由於『人』居處大地,以『食』為天,之所以用
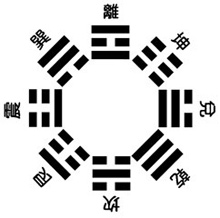
帝 出乎震,齊乎巽,相見乎離,致役乎坤,說言乎兌,戰乎乾,勞乎坎,成言乎艮。萬物出乎震,震,東方也。齊乎巽,巽,東南也。齊也者,言萬物之絜齊也。離也 者,明也。萬物皆相見,南方之卦也。聖人南面而聽天下,嚮明而治,蓋取諸此也。坤也者,地也。萬物皆致養焉,故曰致役乎坤。兌,正秋也,萬物之所說也,故 曰說言乎兌。戰乎乾,乾,西北之卦也,言陰陽相薄也。坎者,水也,正北方之卦也,勞卦也,萬物之所歸也,故曰勞乎坎。艮,東北之卦也,萬物之所成終而所成 始也,故曰成言乎艮。
立八卦耶?儼然一幅『春耕夏耘秋收冬藏』圖!縱將此八卦歸之於『後天』,見得著『兩儀四象』的嗎??若無『陰陽』,那『人』之『太極』將如何『立』呢!!
想『周文王』︰
商朝末年為西伯,故亦稱「伯昌」。任用太顛、散宜生等能人,施行裕民政策,國力日盛,卻為紂所忌,囚之於羑里,囚禁期間 ,寫下周易一書。
何許人也,能寫《周易》,卻不知『八卦之理』,當真是奇也怪哉 ??特此姑妄言之,讀者請姑妄聽之。
天一地二,文王以『人法地』之道,故八卦之旨皆出於
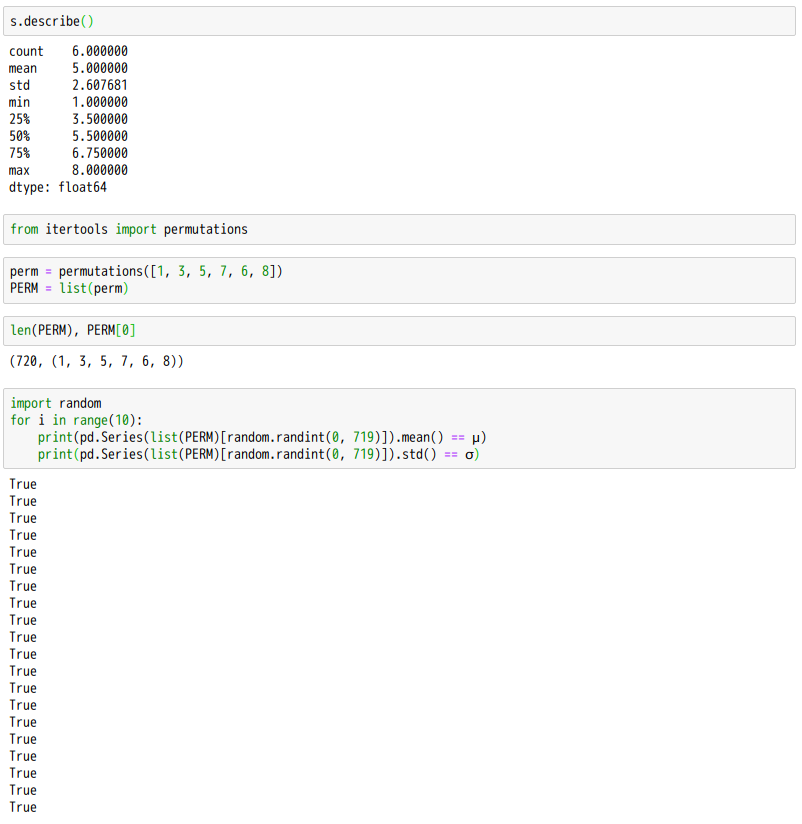
【變貳爻】二十四個
[(坤, 巽), (乾, 坎), (兌, 坤), (巽, 坤), (巽, 離), (兌, 巽), (震, 乾), (艮, 乾),
(離, 坤), (乾, 震), (坎, 乾), (巽, 兌), (震, 坎), (離, 巽), (坤, 兌), (離, 兌),
(艮, 坎), (乾, 艮), (坤, 離), (兌, 離), (坎, 震), (艮, 震), (坎, 艮), (震, 艮)]
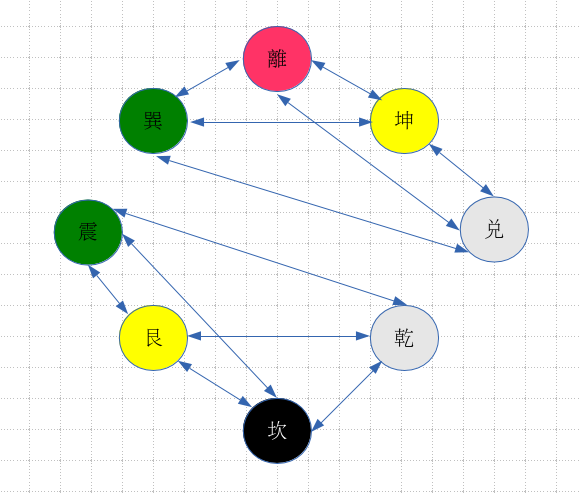
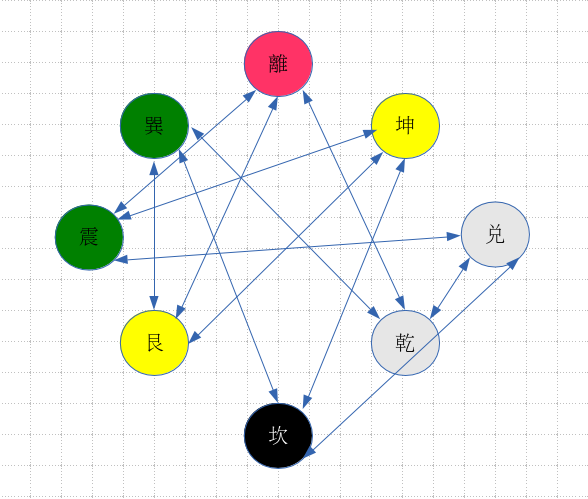
。如果將此關係『圖示』
見著『陰陽』兩儀了沒?果然『類聚群分』,男女授受不親的哩!『先天』以『四象』來調和『陰陽』,『後天』用『五行』去運化『剛柔』。故『震巽』皆木也,有陰陽,『雷風恆』且『風雷益』或祈『風調雨順』乎?此『三爻全變』者也,或以為『生之初』實『難』耶?極『陽』之『動』,方能解『屯難』矣 !!『兌乾』全是金,亦分陰陽,『澤天夬』和『天澤履』或說『吉凶禍福』惟人自招,豈可『怨天尤人』的呢!用『一陽之微 』講『起心動念』之『慎』道,否則『動則得咎』也!!文王豈無說乎??『木金』方可成『器』,『水火』方便為『用』,在這個『後天』『器用人間 』如何『成始成終』的吧!!
【兌乾之秘】
─── 《勇闖新世界︰ 《 PYDATALOG 》【專題】之物件導向設計 ‧四下》
且莫問天下『好人』多?還是『壞的人』多?先思考『平均』之『好人』何謂也!
似講電子帶『負電』,質子帶『正電』,中子『不帶電』嗎??
像說此年、此月、此日…『生男』較之『生女』之多寡嗎!!
僅知『名目』詞條,果能知其『所指』嗎!?
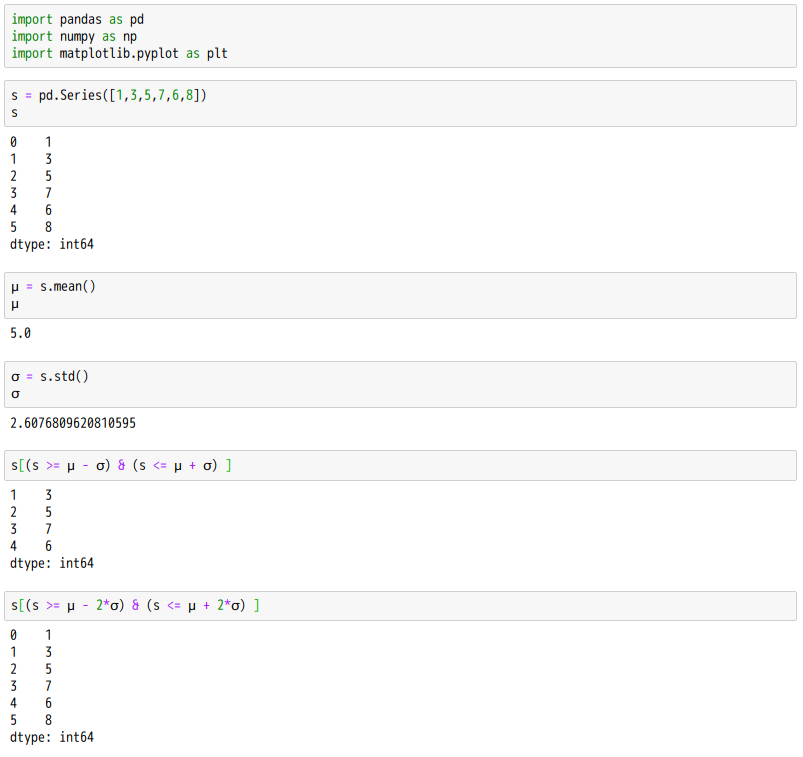
平均數
……
標準差
標準差(又稱標準偏差、均方差,英語:Standard Deviation,縮寫SD),數學符號σ(sigma),在機率統計中最常使用作為測量一組數值的離散程度之用。標準差定義:為變異數開算術平方根,反映組內個體間的離散程度;標準差與期望值之比為標準離差率。測量到分布程度的結果,原則上具有兩種性質:
- 為非負數值(因為開平方後再做平方根);
- 與測量資料具有相同單位(這樣才能比對)。
一個總量的標準差或一個隨機變量的標準差,及一個子集合樣品數的標準差之間,有所差別。其公式如下所列。
標準差的概念由卡爾·皮爾遜引入到統計中。
闡述及應用
簡單來說,標準差是一組數值自平均值分散開來的程度的一種測量觀念。一個較大的標準差,代表大部分的數值和其平均值之間差異較大;一個較小的標準差,代表這些數值較接近平均值。
例如,兩組數的集合{0, 5, 9, 14}和{5, 6, 8, 9}其平均值都是7,但第二個集合具有較小的標準差。
表述「相差k個標準差」,即在 ![]() 的樣本(Sample)範圍內考量。
的樣本(Sample)範圍內考量。
標準差可以當作不確定性的一種測量。例如在物理科學中,做重複性測量時,測量數值集合的標準差代表這些測量的精確度。當要決定測量值是否符合預測值,測量值的標準差佔有決定性重要角色:如果測量平均值與預測值相差太遠(同時與標準差數值做比較),則認為測量值與預測值互相矛盾。這很容易理解,因為如果測量值都落在一定數值範圍之外,可以合理推論預測值是否正確。
標準差應用於投資上,可作為量度回報穩定性的指標。標準差數值越大,代表回報遠離過去平均數值,回報較不穩定故風險越高 。相反,標準差數值越小,代表回報較為穩定,風險亦較小。
母體的標準差
基本定義
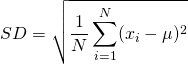
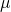 為平均值(
為平均值(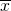 )。
)。
簡易口訣:離均差平方和的平均;方均根。
簡化計算公式
上述公式可以如下代換而簡化︰
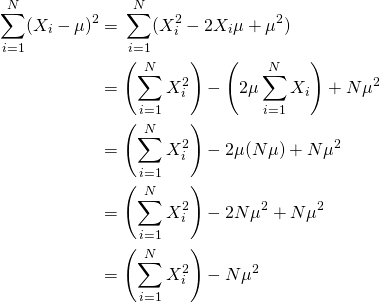
所以︰
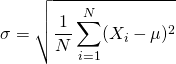
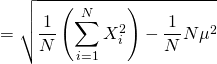
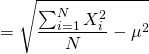
- 根號裡面,亦即變異數(
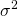 )的簡易口訣為:「平方和的平均」減去「平均的平方」。
)的簡易口訣為:「平方和的平均」減去「平均的平方」。
猶如咬文嚼字就了的呀?!
莫若反思自得呦◎

 ︰
︰