樹莓派、樹莓派之學習、樹莓派之教育

水的生命！！上

金文大篆坎

坎，田野或道路上的坑陷

《説文解字》：坎，陷也。从土，欠聲。

《詩經》魏風．伐檀

坎坎伐檀兮，寘之河之干兮，
河水清且漣猗。
不稼不穡，胡取禾三百廛兮？
不狩不獵，胡瞻爾庭有縣貆兮？
彼君子兮，不素餐兮！

坎坎伐輻兮，寘之河之側兮，
河水清且直猗。
不稼不穡，胡取禾三百億兮？
不狩不獵，胡瞻爾庭有縣特兮？
彼君子兮，不素食兮！

坎坎伐輪兮，寘之河之漘兮，
河水清且淪猗。
不稼不穡，胡取禾三百囷兮？
不狩不獵，胡瞻爾庭有縣鶉兮？
彼君子兮，不素飧兮！

假使從『十進制』的『無窮小數』 x=0. a_1 a_2 a_3 \cdots a_n \overline{b_1 b_2 b_3 \cdots b_m } 的觀點來看，所有的『有理數』 \frac{p}{q} ，如果不是『有限小數』，就一定是『循環小數』。這是因為 q 的餘數只能是 0, \cdots, (q-1)，既然說這個『除法』不是『有限的』步驟，也就是說其間不能夠『整除』 ── 餘數為零 ──，那麼不超過 q 次，終究會出現『第一次』相同的『餘數』，此時『接續』的除法自然開始『重複』，所以必然就是『循環小數』的了！或許『循環』也可以看成有『周期性』出現的吧！！反過來說一個『循環小數』也一定能夠表示成『有理數』，假有我們將 x 乘上 {10}^n 就可以得到 {10}^n x = a_1 a_2 a_3 \cdots a_n . \overline{b_1 b_2 b_3 \cdots b_m }，然而 a_1 a_2 a_3 \cdots a_n 已是『整數』，故可以不必考慮。假設 y = . \overline{b_1 b_2 b_3 \cdots b_m } 是那個『循環小數』的部分，那麼 {10}^m y = b_1 b_2 b_3 \cdots b_m . \overline{b_1 b_2 b_3 \cdots b_m }，因此 \left( {10}^m - 1 \right) y = b_1 b_2 b_3 \cdots b_m，於是 y = \frac{b_1 b_2 b_3 \cdots b_m}{ {10}^m - 1}。所以從 {10}^n x = a_1 a_2 a_3 \cdots a_n + y，可以得到 x = \frac{ a_1 a_2 a_3 \cdots a_n + \frac{b_1 b_2 b_3 \cdots b_m}{ {10}^m - 1}}{{10}^n } 這個『有理數』的啊！！

如果我們換用『物理量』 X 的『量測觀點』來講 X \pm \epsilon，此處的 \epsilon 是『測量』可能引發的『誤差值』。假使 X 與 \epsilon 都可以表現為『有理數』，假設 \epsilon = \frac{P}{Q}，此處 Q 是一個『很大』的整數，那麼它的『最小誤差』也得是 \pm \frac{1}{Q}，這是因為『整數』 P 的『離散性』不得不導致的結論， P 的『前一數』和『後一數』只能是 P \pm 1。

一八七四年『坎特爾』 Cantor 證明了『所有代數數』所構成的『集合』，也是『可數的』無限大。這有什麼重要的嗎？如果再次細思『劉維爾定理』

如果『無理數』 \alpha 是一個 n 次『多項式』之根的『代數數』，那麼存在一個『實數』 A > 0，對於所有的『有理數』 \frac{p}{q}, \ p, q \in \mathbb{Z}, \ \wedge \ q > 0 都有 \left\vert \alpha - \frac{p}{q} \right\vert > \frac{A}{q^n}。

。這是說對一個『代數數』 的『無理數』來講，它與『有理數』 \frac{P}{Q} 的『距離』也許可以說『更遠』或者講『更近』 \left\vert \alpha - \frac{P}{Q} \right\vert > \frac{A}{Q^n}, \ A<1。然而假使 n >1 的話，Q \approx \infty, \ \frac{Q}{Q^n} \approx 0，其實這也就是『無窮小』和『無限大』要如何議論『等級』的『問題』的啊！這樣說的話，當『實數』 R 去掉了『有理數』 Q，再去掉了『代數數』 A，這個 R - Q - A 的集合怎又可能是『可數的』呢？就算是『不可數』也怕會是『坑坑洞洞』的吧！！因此講那個『處處連續』、『無處可微分』以及『咫尺即天涯』之用實數『極限』的『科赫雪花』，恐怕是講著『分析』或也許說『解析』的『複雜』與『困難』代表的了！終將人們帶進了『撲朔迷離』的境遇的吧！就像是為甚麽又會有『邏輯必然』，但卻是『理解困難』的事情呢？？

如果一個點就能夠將實數分割成三部分 (- \infty, r), \{r\}, (r, \infty)，那麼兩個實數間的『連續性』探討，豈非不是『難以議論』的事情呢？就讓我們『對比』著觀察一下的吧？

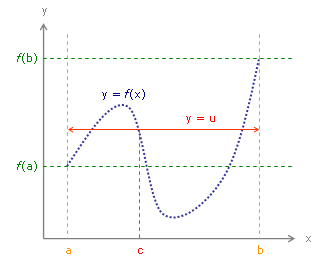
The theorem may be proved as a consequence of the completeness property of the real numbers as follows:

We shall prove the first case f(a) < u < f(b); the second is similar. Let S be the set of all x in [a, b] such that f(x) ≤ u. Then S is non-empty since a is an element of S, and S is bounded above by b. Hence, by completeness, the supremum c = sup S exists. That is, c is the lowest number that is greater than or equal to every member of S. We claim that f(c) = u. Fix some ε > 0. Since f is continuous, there is a δ > 0 such that | f(x) − f(c) | < ε whenever | x − c | < δ. This means that f(x) − ε < f(c) < f(x) + ε for all x between c − δ and c + δ. By the properties of the supremum, there are x between c − δ and c that are contained in S, so that for those x, f(c) < f(x) + ε ≤ u + ε. All x between c and c + δ are not contained in S, so that for those x, f(c) > f(x) − ε > u − ε. Both inequalities u − ε < f(c) < u + ε are valid for all ε > 0, from which we deduce f(c) = u as the only possible value, as stated.

Intermediatevaluetheorem

介值定理

Let f be a continuous function on [a, b] such that f(a)<0 while f(b)>0. Then there exists a point c \in [a,b] such that f(c)=0.

The proof proceeds as follows. Let N be an infinite hyperinteger. Consider a partition of [a,b] into N intervals of equal length, with partition points x_i as i runs from 0 to N. Consider the collection I of indices such that f(xi)>0. Let i_0 be the least element in I (such an element exists by the transfer principle, as I is a hyperfinite set). Then the real number

c=\mathrm{st}(x_{i_0})

is the desired zero of f.

這樣『連續』或者『不連續』概念之『清晰度』的『辨別』，果真能是與『語言文字』相關的嗎？假使說 f(x_0 - \delta x) \cdot f(x_0 + \delta x) < 0 那麼不該是 f(x_0) \approx 0 的嗎？畢竟也只有 \pm \delta x \approx 0 的吧！難道 st\left[ \pm (r \pm \delta r) \right] 不是 \pm r 的嗎？如果這兩者相等 + r = - r，又怎麼可能不是個『零』的呢？？