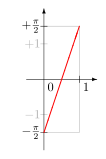
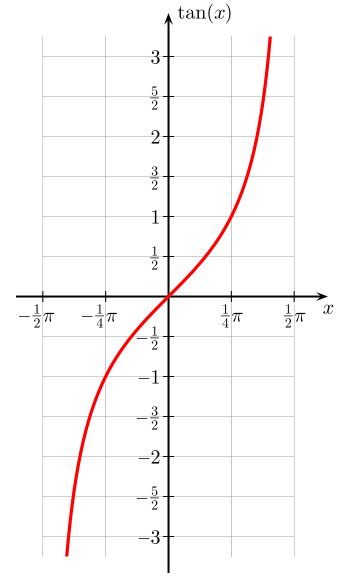
如果說任何一個『開區間』 ![]() ,無論
,無論 ![]() 再小,都可以『一一對應』整體實數,是否會讓人『驚訝』的呢?也就是說一個『開區間』與整體『實數』是一樣『等級』之『無限大』的啊!!舉個例說
再小,都可以『一一對應』整體實數,是否會讓人『驚訝』的呢?也就是說一個『開區間』與整體『實數』是一樣『等級』之『無限大』的啊!!舉個例說 ![]() 將
將 ![]() 的區間,一一對應到了整體實數。假使將整體『實數』表達成
的區間,一一對應到了整體實數。假使將整體『實數』表達成
![]()
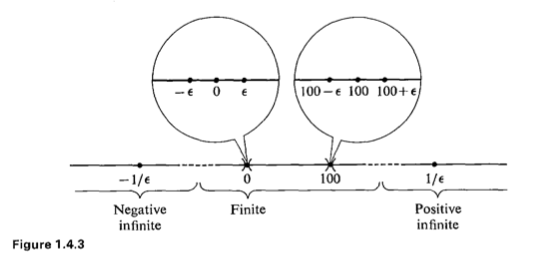
,此處 ![]() 是一個包含著『端點』的『閉區間』。通常數學中有關『實數性質』的『分析』經常用著『開閉區間』來『論證』。從『自然數』是『可數的』無限大來看,『實數』可由可『列舉』 enumerate 的無窮多個『區間』之『聯集』構成。
是一個包含著『端點』的『閉區間』。通常數學中有關『實數性質』的『分析』經常用著『開閉區間』來『論證』。從『自然數』是『可數的』無限大來看,『實數』可由可『列舉』 enumerate 的無窮多個『區間』之『聯集』構成。
假使 ![]() 是『有理數』,
是『有理數』,![]() 也是一個『有理數』,而且
也是一個『有理數』,而且 ![]() ,這是『有理數』的『可分性』,也就是說任『兩個不等』的『有理數』之間『存在』另一個『有理數』,雖然『有理數』能夠無限的『密集』,它也只不過是『可數的』無限大。然而這種『密集性』不僅僅可以用來『逼近』一個『實數』,更可以藉著『不等式』與『整數』的『離散性』 ── 相鄰兩個『整數』
,這是『有理數』的『可分性』,也就是說任『兩個不等』的『有理數』之間『存在』另一個『有理數』,雖然『有理數』能夠無限的『密集』,它也只不過是『可數的』無限大。然而這種『密集性』不僅僅可以用來『逼近』一個『實數』,更可以藉著『不等式』與『整數』的『離散性』 ── 相鄰兩個『整數』 ![]() 之間不存在另一個『整數』 ── 來論證種種『實數性質』,這也說明了『不等式』在『數學分析』裡的『重要性』。就像在『劉維爾數』
之間不存在另一個『整數』 ── 來論證種種『實數性質』,這也說明了『不等式』在『數學分析』裡的『重要性』。就像在『劉維爾數』 ![]() 是個『無理數』的證明裡
是個『無理數』的證明裡
假使它不是一個『無理數』,那麼 ![]() 。 要是取足夠大的
。 要是取足夠大的 ![]() 使得
使得 ![]() ,在
,在 ![]() 時有
時有
![]()
![]() ,因此就與它的定義發生矛盾。
,因此就與它的定義發生矛盾。
為什麼沒有提及『萬一』 ![]() 的情況的呢?因為此時
的情況的呢?因為此時 ![]() ,這就違背了『劉維爾數』
,這就違背了『劉維爾數』 ![]() 的定義。又為什麼可以得到
的定義。又為什麼可以得到 ![]() 的呢?由於
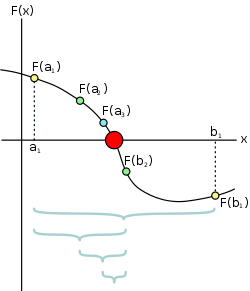
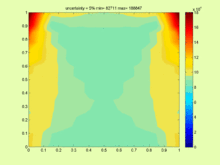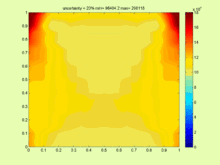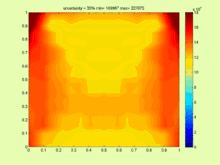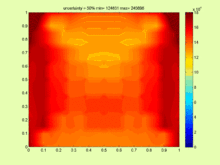
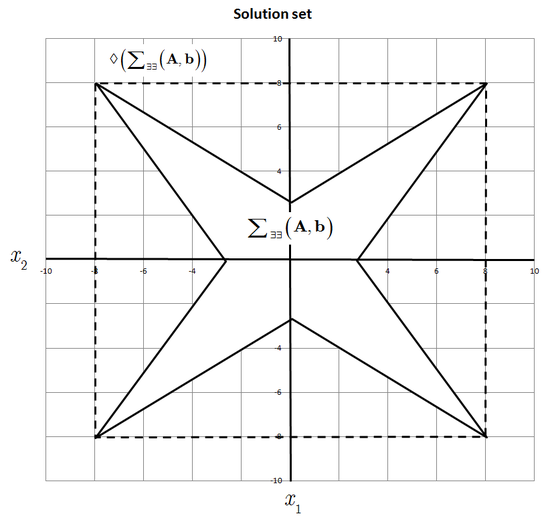
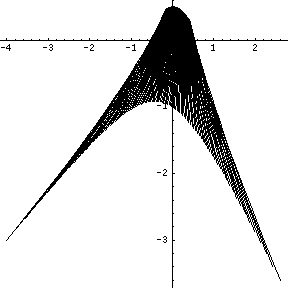
的呢?由於 ![]() 是『整數』,所以它的『差值』至少是個『一』之故。因此對於『不等式』而言,『等號』的『有無』有時是很不相同的,就像『開區間』與『閉區間』的性質也並不相同一樣。從觀察左圖就可以知道,『不等式』構成的『方程式』一般在『求解』上其實是非常『複雜的』。
是『整數』,所以它的『差值』至少是個『一』之故。因此對於『不等式』而言,『等號』的『有無』有時是很不相同的,就像『開區間』與『閉區間』的性質也並不相同一樣。從觀察左圖就可以知道,『不等式』構成的『方程式』一般在『求解』上其實是非常『複雜的』。
在《λ 運算︰計物數《上》》一文中,我們說到『皮亞諾』 Peano 提出了『自然數』之五條公設的系統。用著『未定義』的『基元』數『零 0』,以及『後繼數』successor 的『概念』,打造了『一階算術』系統,現今稱之為『皮亞諾算術系統』。在《布林代數》文章裡,我們對比了『布林代數』、『集合論』與『邏輯學』之間的『密切關係』。整個『布林代數』是可以建立在一個二元運算『孤虛』 ── Sheffer豎線 ![]() ── 之上。也就是說一個『系統』的『公設化』往往不只一種『選擇』,或許是因為雖然兩個看起來『不同』的『概念』,它們彼此之間的『邏輯關係』卻是『等價的』,所以『甲可以推導出乙』,而且『乙能夠演繹出甲』,在此處,我們僅以與『無窮小』概念的『親疏遠近』編排次序,並不論及何者更為『基本』這樣的判斷。
── 之上。也就是說一個『系統』的『公設化』往往不只一種『選擇』,或許是因為雖然兩個看起來『不同』的『概念』,它們彼此之間的『邏輯關係』卻是『等價的』,所以『甲可以推導出乙』,而且『乙能夠演繹出甲』,在此處,我們僅以與『無窮小』概念的『親疏遠近』編排次序,並不論及何者更為『基本』這樣的判斷。
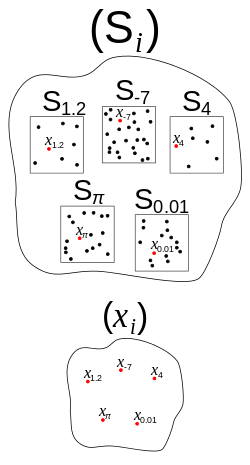
『羅素悖論』在『集合論』的發展史上產生了重大的影響,因此『集合之集合』的構造勢必得『避免矛盾』,『坎特爾』 Cantor 證明了『實數集合』的『元素』是『不可數』的多,這再次引發了如何『列舉』的『難題』,也就是說既然『實數』如果無法『一一指定』,那你又怎麽能夠確定『所說之數』是『存在的』呢?比方說 ![]() 。所以我們從『言之有物』的觀點,就直接『同意』所謂的『選擇公理』︰一個【集合族】是指由非『空集合』
。所以我們從『言之有物』的觀點,就直接『同意』所謂的『選擇公理』︰一個【集合族】是指由非『空集合』 ![]() 所組成的一個『集合』。『存在』著一種【選擇函數】,它是個定義在某個『集合族』
所組成的一個『集合』。『存在』著一種【選擇函數】,它是個定義在某個『集合族』 ![]() 上的函數,對於這個函數來講,所有在『集合族』
上的函數,對於這個函數來講,所有在『集合族』 ![]() 中的『集合元素』
中的『集合元素』 ![]() ,都能夠『選擇』
,都能夠『選擇』 ![]() 。也就是說
。也就是說 ![]() 可以『指定』某一個
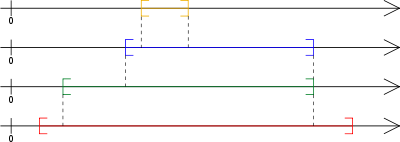
可以『指定』某一個 ![]() 中的『元素』 。這裡所說的『同意』之意思就不過是想要在『直觀』中『簡化』討論之事項,比方講像某些『探討』著一條平面上的『封閉曲線』,它到底是不是能夠將『平面』分割成『曲線內』與『曲線外』之兩個部分的此類『議論』。這樣『實數分析』中所謂的『疊套閉區間』
中的『元素』 。這裡所說的『同意』之意思就不過是想要在『直觀』中『簡化』討論之事項,比方講像某些『探討』著一條平面上的『封閉曲線』,它到底是不是能夠將『平面』分割成『曲線內』與『曲線外』之兩個部分的此類『議論』。這樣『實數分析』中所謂的『疊套閉區間』 ![]()
![]() 的『概念』,就『超實數』
的『概念』,就『超實數』 ![]() 來講,就是『標準部份函數』
來講,就是『標準部份函數』 ![]() ,所以說如果那個
,所以說如果那個 ![]() 的話,一定會有
的話,一定會有 ![]() ,也就是說這就『確定』了那個『實數值』。假使我們換個觀點來看
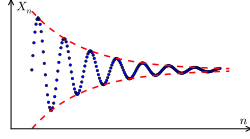
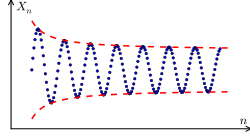
,也就是說這就『確定』了那個『實數值』。假使我們換個觀點來看 ![]() 與
與 ![]() 都各自構成一個了『單調』之『上升』以及『單調』之『下降』的『序列』,而且
都各自構成一個了『單調』之『上升』以及『單調』之『下降』的『序列』,而且 ![]() ,那麼難到不該
,那麼難到不該 ![]() 的嗎?如果說自然界之『物理量』總是來自於『度量』,因此那兩個稱作『柯西序列』 Cauchy sequence 的
的嗎?如果說自然界之『物理量』總是來自於『度量』,因此那兩個稱作『柯西序列』 Cauchy sequence 的 ![]() 的『序列』,它們所『代表』的就是『量測』的『極限分析』的啊!假使用『超整數』與『巨量』
的『序列』,它們所『代表』的就是『量測』的『極限分析』的啊!假使用『超整數』與『巨量』 ![]() 可敘述為
可敘述為 ![]() 。假使設想著對於『可列舉』之物,至少可以說在『無窮遠』處之時﹐『那些‧哪些』的物將會是距離『這麼‧這麼』之『無窮近』的吧?然而對於『不可列舉』之物,我們真的還能夠講述著『某個‧某個』的『什麼』的嗎?因為說不定它還框陷在『難計』的『侑限』裡,你又怎麽可能得到『遠近』之『結論』的呢??或許這就是『有理數』的『可數性』很適合用來『建構』那種『不可數性』的吧!!
。假使設想著對於『可列舉』之物,至少可以說在『無窮遠』處之時﹐『那些‧哪些』的物將會是距離『這麼‧這麼』之『無窮近』的吧?然而對於『不可列舉』之物,我們真的還能夠講述著『某個‧某個』的『什麼』的嗎?因為說不定它還框陷在『難計』的『侑限』裡,你又怎麽可能得到『遠近』之『結論』的呢??或許這就是『有理數』的『可數性』很適合用來『建構』那種『不可數性』的吧!!