艾賓浩斯錯覺

艾賓浩斯錯覺（英文：Ebbinghaus illusion）是一種對實際大小知覺上的錯視。在最著名的錯覺圖中，兩個完全相同大小的圓放置在一張圖上，其中一個圍繞較大的圓，另一個圍繞較小的圓；圍繞大圓的圓看起來會比圍繞小圓的圓還要小。

這一發現便以發現者的名字來命名，發現者為德國心理學家赫爾曼·艾賓浩斯（1850-1909）。

艾賓浩斯錯覺在最近的爭論中（對於以分割路徑存在於大腦中的知覺和行為）扮演了關鍵性角色（詳見視覺皮層）。其主張艾賓浩斯錯覺會扭曲對於大小的知覺，但當需要反應出抓取之類的行為時，便不存在大小上的扭曲（Goodale & Milner, 1992）。然而在最近的研究中（Franz等人, 2005）提出原來的實驗存有瑕疵，其原始刺激限制了在抓取行為中發生錯誤的可能性，因而產生相當準確的抓取反應。並且指出獨立的較大和較小刺激——導致沒有錯覺，因為沒有其它的圓可起到參考作用。法蘭茲等人總結如下，行為和知覺系統兩者同樣受到艾賓浩斯錯覺所愚弄。

圖中兩個橘色圓圈的大小相同，但左邊的橘色圓圈看起來卻比較小。

雖說『眼見為憑』，難保不是『錯覺』呢？

此事因平面國流傳一圖而起︰

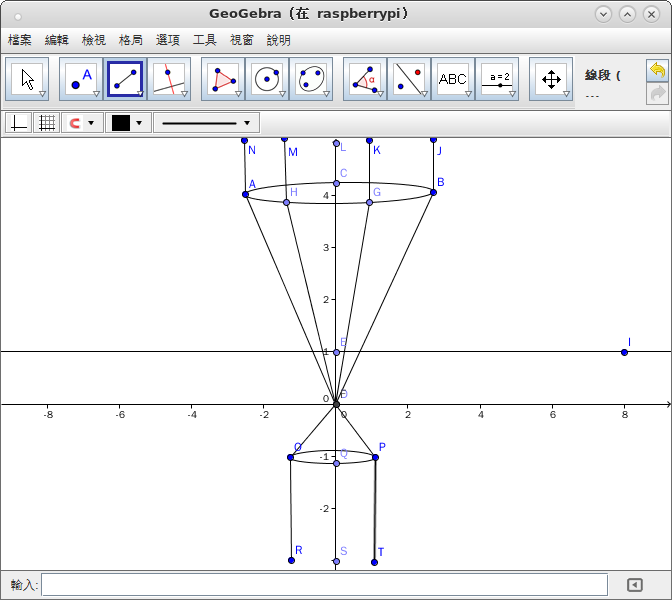
卻納悶平面國似有『透鏡』，恍惚是『平行光轉換器』耶！然懷疑

無厚能有透鏡乎？！

一時浮現惠施之

【無厚不可積也，其大千里。】

論︰

假使從『惟初太始，道立于一』來看『一』的意思，『惠施』所說之『大一』和『小一』中的『一』，不是『多中有一』，而是『此中唯一』。他的『觀點』是沒有『等級之分』的『無限大』與『無窮小』。

『粒子物理學』是研究組成『物質』和『射線』的『基本粒子』和它們之間的『交互作用』之物理學。由於許多的『基本粒子』在大自然中一般條件下『不存在』或者不會『單獨出現』，物理學家只能使用『粒子加速器』在『高能碰撞』的條件下才能產生與研究它們，所以『粒子物理學』也被叫做『高能物理學』。現今科學中這個『物質』的『可分性』研究也持續著『還原論』的『批評』和『論辯』。那麼一個『大一統』的『萬物理論』可能『存在』的嗎？它果真能『解釋』宇宙萬有的『性質』，如此我們只需要一組『方程式』就能夠『認識』古往今來以至於悠悠無盡的『眾生』的嗎？？或許當人們更深入理解『混沌現象』與『量子糾纏』所帶來的『理性衝擊』之時，又或許在求解了『氫原子』、『氧原子』以及『水分子』的量子力學『方程式』後，想要用來『解釋』『水』的諸多『特性』的『可能性』的時候，大概會發現是『雞同鴨講』的吧！！

【無厚不可積也，其大千里。 】

據聞『厚』來自於，在巨大岩體裡開鑿的帝王陵寝，即『崖墓』，墓内設計模仿帝王生前的陽間世界，有大量陪葬品，此即古代所谓的『厚葬』。

《説文解字》：厚，山陵之厚也。从，从厂。垕，古文厚，从后、土。

《 莊子‧內篇‧養生主第三 》

吾生也有涯，而知也無涯。以有涯隨無涯，殆已！已而為知者，殆而已矣！為善無近名，為惡無近刑，緣督以為經，可以保身，可以全生，可以養親，可以盡年。

庖丁為文惠君解牛，手之所觸，肩之所倚，足之所履，膝之所踦，砉然響然，奏刀騞然，莫不中音，合於桑林之舞，乃中經首之會。文惠君曰：「嘻，善哉！技蓋至此乎？」

庖丁釋刀對曰：「臣之所好者道也，進乎技矣。始臣之解牛之時，所見無非全牛者﹔三年之后，未嘗見全牛也﹔方今之時，臣以神遇而不以目視，官知止而神欲行。依乎天理，批大卻，導大窾，因其固然。技經肯綮之未嘗微礙，而況大軱乎！良庖歲更刀，割也﹔族庖月更刀，折也﹔今臣之刀十九年矣，所解數千牛矣，而刀刃若新發於硎。彼節者有閒，而刀刃者無厚，以無厚入有閒，恢恢乎其於游刃必有餘地矣。是以十九年而刀刃若新發於硎。雖然，每至於族，吾見其難為，怵然為戒，視為止，行為遲，動刀甚微，謋然已解，牛不知其死也，如土委地。提刀而立，為之而四顧，為之躊躇滿志，善刀而藏之。」

文惠君曰：「善哉！吾聞庖丁之言，得養生焉。」

公文軒見右師而驚曰：「是何人也？惡乎介也？天與？其人與？」曰：「天也，非人也。天之生是使獨也，人之貌有與也。以是知其天也，非人也。」

澤雉十步一啄，百步一飲，不蘄畜乎樊中。神雖王，不善也。
老聃死，秦失弔之，三號而出。

弟子曰：「非夫子之友邪？」

曰：「然。」

「然則弔焉若此，可乎？」
曰：「然。始也吾以為其人也，而今非也。向吾入而弔焉，有老者哭之，如哭其子﹔少者哭之，如哭其母。彼其所以會之，必有不蘄言而言，不蘄哭而哭者。是遁天倍情，忘其所受，古者謂之遁天之刑。適來，夫子時也﹔適去，夫子順也。安時而處順，哀樂不能入也，古者謂是帝之縣解。」
指窮於為薪，火傳也，不知其盡也。

既然『惠施』是『莊子』的『非同道摯友』，『莊子』講『庖丁解牛』神技中有『彼節者有閒，而刀刃者無厚，以無厚入有閒，恢恢乎其於游刃必有餘地矣。』來看『無厚』一詞的『意指』當是『沒有厚度』。如同『刀』之『刃』是『刀之用』，惟『鋒利』爾，所謂『割』與『折』是『不會用』，『以有砍有』因此才需要『逐年』甚或『逐月』的『換刀』，以其不『鋒利』了，所以才說『刀刃者無厚』。這樣看來『惠施』所言『無外』、『無內』以及『無厚』之『無』字皆指『有的否定』，因此『無厚』就是『厚度是零』。只需要考察 $\lim \limits_{n \to \infty} 0 \cdot n = 0$ ，當然可以知道『零』是『不可積』的。其實此處並沒有那種 $\infty \cdot 0$ 的問題！或許有人尚不明白『無窮小』數並不等於『零』 $\delta x \neq 0$ ，事實上正『無窮小』數大於『零』 $+\delta x >0$ ，要不然它要怎麽滿足『代數法則』的呢？因此才會有『可積不可積』的問題的啊！進一步說，在『代數』的『計算法則』之中『整體等於其部分和』，那麼『無窮小』數果真可能符合這個『法則』的嗎？？也許這就是 $\infty \cdot 0$ 『疑惑』的由來。舉例來說，考慮『分割』一個『閉區間』 $[a, b]$ ，如果我們將它的『長度』記作 $l = b - a$ ，將之『等分』成 $N$ 段 $\Delta x = \frac{l}{N}$ ，其內有 $N - 1$ 個『分割點』，連同兩個『端點』表為 $x_0 = a, \ x_k, \ k=1 \ \cdots \ N -1, \ x_N = b$ ，此時當然 $N \cdot \Delta x = l$ ，假使那個『分割數』 $N$ 成了『巨量』 $H$ 時，難到『分割點距』不會變成『無窮小』數 $\Delta x = \frac{1}{H} = \delta x$ 的嗎？此時難到可能 $H \cdot \delta x \neq l$ 的嗎？？也就是說，『無窮小』數是『有』，而『有』才『可以積』。既然『無窮小』數滿足『代數法則』，定然滿足推論中所用之『限定』的『代數關係式』 $N \cdot \Delta x = l \Longrightarrow H \cdot \delta x =l$ ，這應該是很自然的吧！！

─── 摘自《【Sonic π】電聲學之電路學《四》之《 !! 》》

且不管人世間『不知為不知』之說，揣想著平面國之『邏輯』應能『自圓其說』之理。

此或為『平投‧點投』的『聚焦義』吧︰

人類是使用符號的動物，故而能以語言、文字表述宇宙人生之萬象。然而這並非不學而能的事，實是成長學習過程中，日積月累之功。因此運用『矩陣光學』符號，展現『幾何光學』事理，不如想像之簡單容易，一般還得努力練習的哩？好處是熟悉之後對於『幾何光學』之理解也自然深化的了！

茲舉何謂『焦距』乙事，談談『平行光成像』之理︰

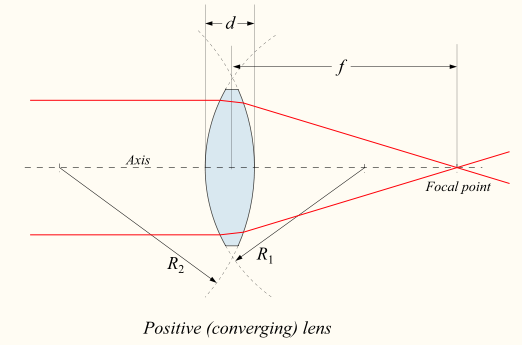
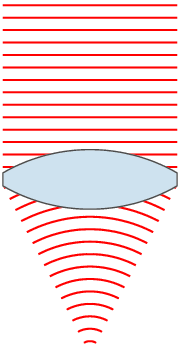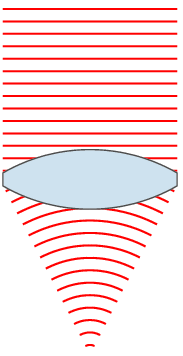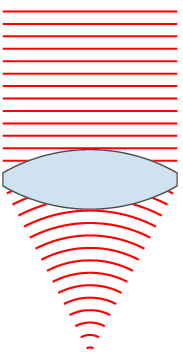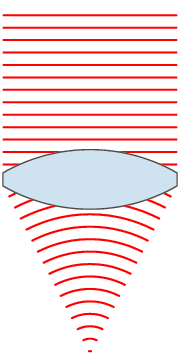
Lens_and_wavefronts Large_convex_lens

若問什麼是『平行光』？它與什麼『平行』的呢？？一束『平行』之光線，可用 $(h, \theta)$ ，這裡 $h$ 表示距離『光軸』的高度，視為此束『平行光』之參數變元；那個 $\theta$ 是此光束與『光軸』形成的夾角，因此為此束『平行光』之常數常元。因是『平行光』說其自身光線彼此平行而已。

…

如此就一個『焦距』為 $f$ 的『薄透鏡』

$\left( \begin{array}{cc} 1 & 0 \\ - \frac{1}{f} & 1 \end{array} \right)$

，意味著與『光軸平行』之『平行光』 $\theta = 0$ 行經此『薄透鏡』後，將在離『薄透鏡』 $f$ 處『聚焦』，此點稱之為『焦點』。看來清楚明白之事，數理解析上要如何陳述此理耶？設想此束『平行光』剛過『薄透鏡』即將折屈，一段距離 $z$ 後，整束光會交匯於一點，也就是說此點存在且和 $h$ 無關也！且用 Sympy 工具幫忙運算一番︰

pi@raspberrypi:~ h \cdot \left( 1 - \frac{z}{f} \right) + z \cdot \theta z = f h\theta = 00f(0, \theta)f \left( \begin{array}{cc}

1 & 0 \\

- \frac{1}{f} & 1 \end{array} \right) \to \inftyI_2$


單位矩陣
在線性代數中， $n$ 階單位矩陣，是一個 $n\times n$ 的方形矩陣，其主對角線元素為1，其餘元素為0。單位矩陣以 $I_n$ 表示；如果階數可忽略，或可由前後文確定的話，也可簡記為 $I$ （或者E）。（在部分領域中，如量子力學，單位矩陣是以粗體字的1表示，否則無法與 $I$ 作區別。）

 $I_{1}={\begin{bmatrix}1\end{bmatrix}},\ I_{2}={\begin{bmatrix}1&0\\0&1\end{bmatrix}},\ I_{3}={\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}},\ \cdots ,\ I_{n}={\begin{bmatrix}1&0&\cdots &0\\0&1&\cdots &0\\\vdots &\vdots &\ddots &\vdots \\0&0&\cdots &1\end{bmatrix}}$ 

一些數學書籍使用 $U$ 和 $E$ （分別意為「單位矩陣」和「基本矩陣 」），不過I更加普遍。
特別是單位矩陣作為所有 $n$ 階矩陣的環的單位，以及作為由所有 $n$ 階可逆矩陣構成的一般線性群 $GL(n)$ 的單位元素（單位矩陣明顯可逆，單位矩陣乘自己，仍是單位矩陣）。
這些 $n$ 階矩陣經常表示來自 $n$ 維向量空間自己的線性變換， $I_n$ 表示恆等函數，而不理會基。
有時使用這個記法簡潔的描述對角線矩陣，寫作：

 $I_{n}={\mathrm {diag}}(1,1,...,1)$ 

也可以克羅內克爾δ記法寫作：

 $(I_{n})_{{ij}}=\delta _{{ij}}$ 

的嘛◎

日	一	二	三	四	五	六
« 4 月
			1	2	3	4
5	6	7	8	9	10	11
12	13	14	15	16	17	18
19	20	21	22	23	24	25
26	27	28	29	30	31

FreeSandal

GoPiGo 小汽車︰格點圖像算術《投影幾何》【四‧平面國】《補丁》

艾賓浩斯錯覺

單位矩陣

輕。鬆。學。部落客