派︰昔有『 Thue 』者，其言曰︰

阿克塞爾‧圖厄【挪威語 Axel Thue】一位數學家，以研究丟番圖用『有理數』逼近『實數』問題以及開拓『組合數學』之貢獻而聞名。他於一九一四發表了『詞之群論問題』Word problem for group 啟始了一個今天稱之為『字串改寫系統』SRS String Rewriting System 的先河，如從現今的研究和發現來看，它與圖靈機的『停機問題』密切相關。上個千禧年之時，John Colagioia 用『Semi-Thue System』寫了一個『奧秘的』 esoteric 程式語言 Thue ，作者宣稱︰

Thue represents one of the simplest possible ways to construe 『constraint-based』基於約束 programming. It is to the constraint-based 『paradigm』典範 what languages like『 OISC 』── 單指令集電腦 One instruction set computer ── are to the imperative paradigm; in other words, it’s a 『tar pit』焦油坑.

，果然概念廣大能通天！！『 SRS 』卻是個『奧秘語言』？？

生︰ 當真是︰ ☆★ 之火，可以燎原。能不精思實念乎？

人類的思維如果一旦不『審慎』，很容易邏輯『混亂』，以至於言論多所『謬誤』，有時或許『巧說詭辯』。比方說公孫龍子的『雞三足』之詭論︰…牛羊有毛，雞有羽。謂雞足一，數足二；二而一，故三。謂牛羊足一，數足四；四而一，故五。羊牛足五，雞足三，故曰：『牛合羊非雞』。非，有以非雞也。…裡頭的『謂雞足一』之『雞足』和『一』是什麼？『數足二』的『足』與『二』又是什麼？卻能相加，彷彿『一雞 + 二足』可以得到『三 』的一般？！已經完全不像他的『白馬非馬論』了。

洛基的賭注 Loki’s Wager
洛基乃北歐神話中以『詐騙』著名之神。傳說他曾與矮人打賭卻輸了。當矮人們依約來『提頭』時，洛基說︰『沒問題』，但是必須依照『約定』，只能取走『他的頭』，而不能動著『他的脖子』。於是彼此開始『爭論』該如何的『切割』：有哪些部分雙方同意『是頭』；又有哪些部分認同『是脖子』。只是脖子的『結束點』和頭之『開始點』究竟『是哪裡』，互相一直無法『取得共識』。於是洛基終於保住著了他的頭。

── 摘自《M♪o 之學習筆記本《丑》控制︰【黑水北】當思恒念》

當『數理』失卻了『參考系』確定『概念』之意義；宛如憑空地述說著『群論』可以將一元多次方程式可解性的問題連繫起來，豈非囫圇吞棗乎？不知滋味之物要怎樣講耶？？

且思『近』之『視角大』、『遠』之『視角小』是『歐式幾何』之『性質』嗎？

可以得到

然而『天很高，日很遠』，因此 ，故而很難『度量』的『精準』，一點點『角度』之『誤差』就產生了那個

失之豪釐，差以千里

的吧！！

─── 摘自《失之豪釐，差以千里！！《上》》

難到『有限高度』 之物，若位在『無窮遠』 處，竟然它的『視角』 能不趨近於『零』   嗎？？

就像『眼見之實』

消失點

如當你沿著鐵路線去看兩條鐵軌，沿著公路線去看兩邊排列整齊的樹木時，兩條平行的鐵軌或兩排樹木連線交與很遠很遠的某一點，這點在透視投影中叫做消失點。

藝術家和工程師在紙上表現立體圖時，常用一種透視法，這種方法源於人們的視覺經驗：大小相同的物體，離你較近的看起來比離你較遠的大。凡是平行的直線都消失於無窮遠處的同一個點，消失於視平線上的點的直線都是水平直線。

之『現象文字』及『理論內容』的陳述

Vanishing point

In graphical perspective, a vanishing point is an abstract point on the image plane where 2D projections (or drawings) of a set of parallel lines in 3D space appear to converge.^{[clarification needed]} When the set of parallel lines is perpendicular to a picture plane, the construction is known as one-point perspective, and their vanishing point corresponds to the oculus, or “eye point”, from which the image should be viewed for correct perspective geometry.^[1] Traditional linear drawings use objects with one to three sets of parallels, defining one to three vanishing points.

A 2D construction of perspective viewing, showing the formation of a vanishing point

需要『想像』呦！

The vanishing point may also be referred to as the “direction point”, as lines having the same directional vector, say D, will have the same vanishing point or converge at the same vanishing points. Mathematically, let q ≡ (x, y, f) be a point lying on the image plane, where f is the focal length (of the camera associated with the image), and let v_q ≡ (x/h, y/h, f/h) be the unit vector associated with q, where h = √x² + y² + f². If we consider a straight line in space S with the unit vector n_s ≡ (n_x, n_y, n_z) and its vanishing point v_s, the unit vector associated with v_s is equal to n_s, assuming both are assumed to point towards the image plane.^[2]

When the image plane is parallel to two world-coordinate axes, lines parallel to the axis which is cut by this image plane will meet at infinity i.e. at the vanishing point. Lines parallel to the other two axes will not form vanishing points as they are parallel to the image plane. This is one-point perspective. Similarly, when the image plane intersects two world-coordinate axes, lines parallel to those planes will meet at infinity and form two vanishing points. This is called two-point perspective. In three-point perspective the image plane intersects the x, y, and z axes and therefore lines parallel to these axes intersect, resulting in three different vanishing points.

不知可否借假修真的哩◎

差不多先生傳‧胡適

你知道中國最有名的人是誰？提起此人，人人皆曉，處處聞名，他姓差，名不多，是各省各縣各村人氏。你一定見過他，一定聽過別人談起他，差不多先生的名字，天天掛在大家的口頭，因為他是中國全國人的代表。

差不多先生的相貌，和你和我都差不多。他有一雙眼睛，但看的不很清楚；有兩隻耳朵，但聽的不很分明；有鼻子和嘴，但他對於氣味和口味都不很講究；他的腦子也不小，但他的記性卻不很精明，他的思想也不細密。

他常常說：「凡事只要差不多，就好了。何必太精明呢？」

他小時候，他媽叫他去買紅糖，他買了白糖回來，他媽罵他，他搖搖頭道：「紅糖，白糖，不是差不多嗎？」

他在學堂的時候，先生問他：「直隸省的西邊是哪一省？」他說是陝西。先生說：「錯了，是山西，不是陝西。」他說：「陝西同山西，不是差不多嗎？」

後來他在一個錢鋪裏做夥計；他也會寫，也會算，只是總不會精細 ；十字常常寫成千字，千字常常寫成十字。掌櫃的生氣了，常常罵他，他只笑嘻嘻地賠小心道：「千字比十字多一小撇，不是差不多嗎？」

有 一天，他為了一件要緊的事，要搭火車到上海去，他從從容容地走到火車站，遲了兩分鐘，火車已開走了。他白瞪著眼，望著遠遠的火車上的煤煙，搖搖頭道：「只 好明天再走了，今天走同明天走 ，也還差不多；可是火車公司未免太認真了。八點三十分開，同八點三十二分開，不是差不多嗎？」他一面說，一面慢慢地走回家，心裏總不很明白為甚麼火車不肯 等他兩分鐘。

有 一天，他忽然得一急病，趕快叫家人去請東街的汪先生。那家人急急忙忙跑去，一時尋不著東街的汪大夫，卻把西街的牛醫王大夫請來了。差不多先生病在脇上，知 道尋錯了人；但病急了，身上痛苦，心裏焦急，等不得了，心裏想道：「好在王大夫同汪大夫也差不多，讓他試試看罷。」於是這位牛醫王大夫走近脇前，用醫牛的 法子給差不多先生治病。不上一點鐘，差不多先生就一命嗚呼了。

差不多先生差不多要死的時候，一口氣斷斷續續地說道：「活人同死人也差……差……差……不多，……凡事只要……差……差……不多……就……好了，何……必……太……太認真呢？」他說完了這句格言，就絕了氣。

他死後，大家都很稱讚差不多先生樣樣事情看得破，想得通；大家都說他一生不肯認真，不肯算帳，不肯計較，真是一位有德行的人 。於是大家給他取個死後的法號，叫他做圓通大師。

他的名譽愈傳愈遠，愈久愈大，無數無數的人，都學他的榜樣，於是人人都成了一個差不多先生。──然而中國從此就成了一個懶人國了。

試想『相機』所見與『隻眼』相同嗎？之前《光的世界》系列文本已嚐試解說過很多『光學系統』問題哩！

若問看似簡單的『針孔相機模型』

Pinhole camera model

The pinhole camera model describes the mathematical relationship between the coordinates of a 3D point and its projection onto the image plane of an ideal pinhole camera, where the camera aperture is described as a point and no lenses are used to focus light. The model does not include, for example, geometric distortions or blurring of unfocused objects caused by lenses and finite sized apertures. It also does not take into account that most practical cameras have only discrete image coordinates. This means that the pinhole camera model can only be used as a first order approximation of the mapping from a 3D scene to a 2D image. Its validity depends on the quality of the camera and, in general, decreases from the center of the image to the edges as lens distortion effects increase.

Some of the effects that the pinhole camera model does not take into account can be compensated, for example by applying suitable coordinate transformations on the image coordinates, and other effects are sufficiently small to be neglected if a high quality camera is used. This means that the pinhole camera model often can be used as a reasonable description of how a camera depicts a 3D scene, for example in computer vision and computer graphics.

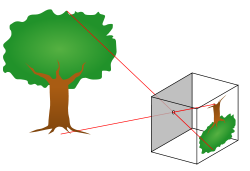
A diagram of a pinhole camera.

The geometry and mathematics of the pinhole camera

NOTE: The x₁x₂x₃ coordinate system in the figure is left-handed, that is the direction of the OZ axis is in reverse to the system the reader may be used to.

The geometry related to the mapping of a pinhole camera is illustrated in the figure. The figure contains the following basic objects:

• A 3D orthogonal coordinate system with its origin at O. This is also where the camera aperture is located. The three axes of the coordinate system are referred to as X1, X2, X3. Axis X3 is pointing in the viewing direction of the camera and is referred to as the optical axis, principal axis, or principal ray. The 3D plane which intersects with axes X1 and X2 is the front side of the camera, or principal plane.
• An image plane where the 3D world is projected through the aperture of the camera. The image plane is parallel to axes X1 and X2 and is located at distance  from the origin O in the negative direction of the X3 axis. A practical implementation of a pinhole camera implies that the image plane is located such that it intersects the X3 axis at coordinate -f where f > 0. f is also referred to as the focal length^{[citation needed]} of the pinhole camera.
• A point R at the intersection of the optical axis and the image plane. This point is referred to as the principal point or image center.
• A point P somewhere in the world at coordinate relative to the axes X1,X2,X3.
• The projection line of point P into the camera. This is the green line which passes through point P and the point O.
• The projection of point P onto the image plane, denoted Q. This point is given by the intersection of the projection line (green) and the image plane. In any practical situation we can assume that  > 0 which means that the intersection point is well defined.
• There is also a 2D coordinate system in the image plane, with origin at R and with axes Y1 and Y2 which are parallel to X1 and X2, respectively. The coordinates of point Q relative to this coordinate system is .

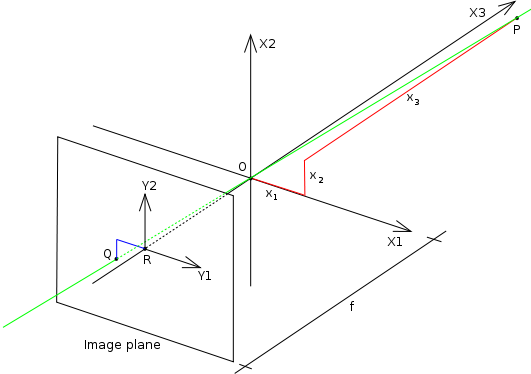
The geometry of a pinhole camera

The pinhole aperture of the camera, through which all projection lines must pass, is assumed to be infinitely small, a point. In the literature this point in 3D space is referred to as the optical (or lens or camera) center.^[1]

Next we want to understand how the coordinates  of point Q depend on the coordinates  of point P. This can be done with the help of the following figure which shows the same scene as the previous figure but now from above, looking down in the negative direction of the X2 axis.

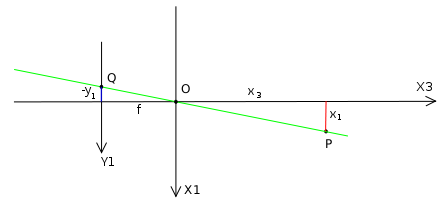
The geometry of a pinhole camera as seen from the X2 axis

In this figure we see two similar triangles, both having parts of the projection line (green) as their hypotenuses. The catheti of the left triangle are  and f and the catheti of the right triangle are  and  . Since the two triangles are similar it follows that

or 

A similar investigation, looking in the negative direction of the X1 axis gives

or 

This can be summarized as

which is an expression that describes the relation between the 3D coordinates of point P and its image coordinates  given by point Q in the image plane.

─── 摘自《光的世界︰矩陣光學二》

，為什麼沒有介紹其實際矩陣運算的呢？？

因為那時就勢必得進入

投影平面

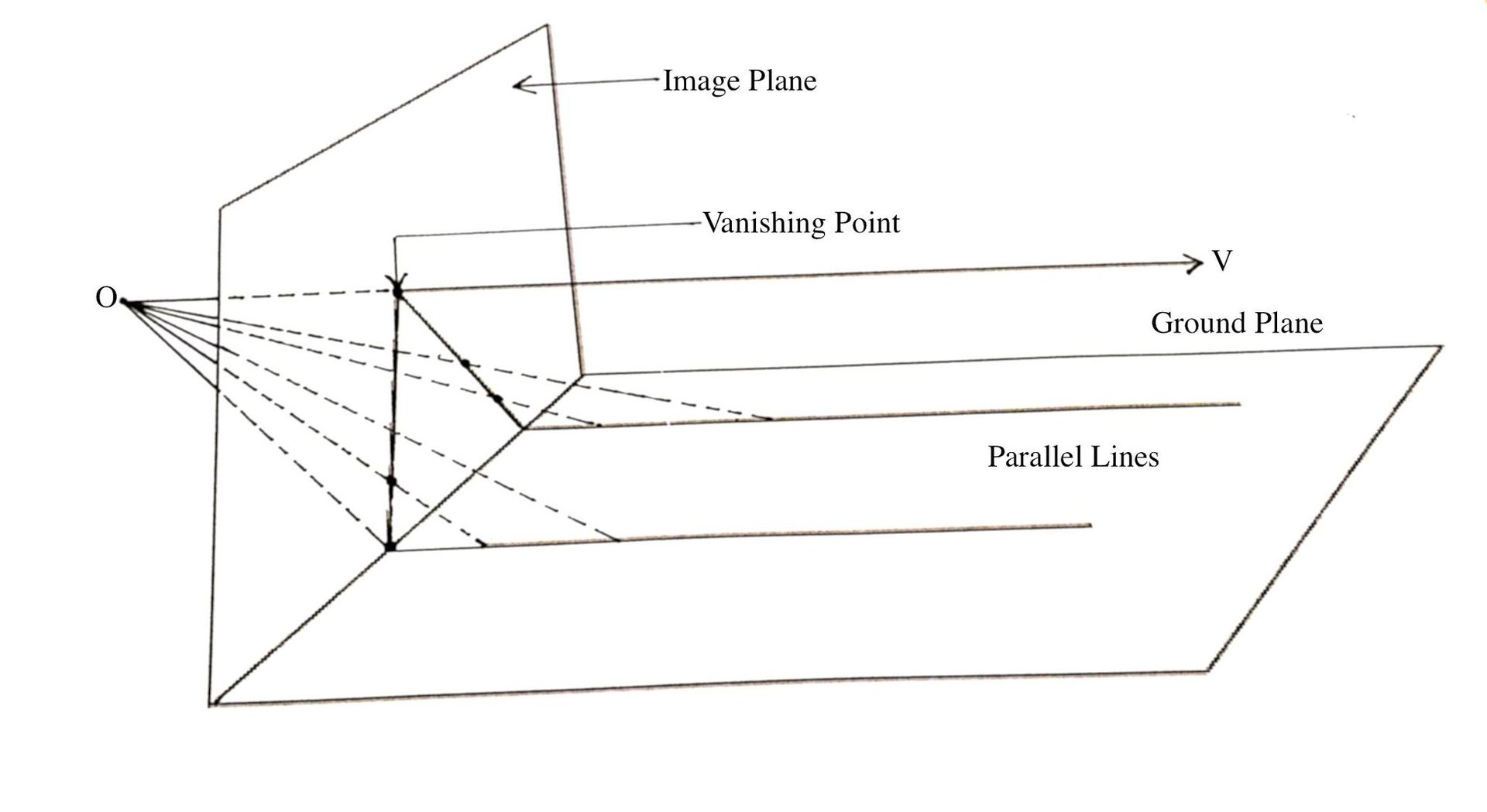
在數學裡，投影平面（projective plane）是一個延伸平面概念的幾何結構。在普通的歐氏平面裡，兩條線通常會相交於一點，但有些線（即平行線）不會相交。投影平面可被認為是個具有額外的「無窮遠點」之一般平面，平行線會於該點相交。因此，在投影平面上的兩條線會相交於一個且僅一個點。

文藝復興時期的藝術家在發展透視投影的技術中，為此一數學課題奠定了基礎。投影平面的典型範例為實投影平面，亦稱為「擴展歐氏平面」。此一範例在代數幾何、拓撲學及投影幾何內都很重要，在各領域內的形式均略有不同，可標計為 PG(2, R)、RP² 或 P₂(R) 等符號。還有許多其他的投影平面，包括無限（如複投影平面）與有限（如法諾平面）之類型。

投影平面是二維投影空間，但並不是所有投影平面都可以嵌入三維投影空間內。投影平面是否能嵌入三維投影空間取決於該平面是否為笛沙格平面。

兩條平行線似乎相交於「無窮遠處」的消失點。在投影平面裡，這是真的。

※ 註

笛沙格定理

笛沙格（Desargues）定理說明：在射影空間中，有六點A,B,C,a,b,c。Aa,Bb,Cc共點若且唯若AB∩ab,BC∩bc,CA∩ca共線。

在射影幾何的對偶性來看，笛沙格定理是自對偶的。

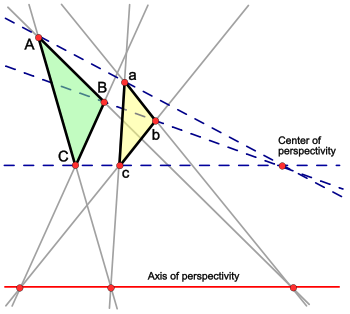
也！！

要如何簡易講此『實射影平面』乎？？

Real projective plane

In mathematics, the real projective plane is an example of a compact non-orientable two-dimensional manifold; in other words, a one-sided surface. It cannot be embedded in standard three-dimensional space without intersecting itself. It has basic applications to geometry, since the common construction of the real projective plane is as the space of lines in R³ passing through the origin.

The plane is also often described topologically, in terms of a construction based on the Möbius strip: if one could glue the (single) edge of the Möbius strip to itself in the correct direction, one would obtain the projective plane. (This cannot be done in three-dimensional space.) Equivalently, gluing a disk along the boundary of the Möbius strip gives the projective plane. Topologically, it has Euler characteristic 1, hence a demigenus (non-orientable genus, Euler genus) of 1.

Since the Möbius strip, in turn, can be constructed from a square by gluing two of its sides together, the real projective plane can thus be represented as a unit square (that is, [0,1] × [0,1] ) with its sides identified by the following equivalence relations:

(0, y) ~ (1, 1 − y)   for 0 ≤ y ≤ 1

and

(x, 0) ~ (1 − x, 1)   for 0 ≤ x ≤ 1,

as in the leftmost diagram on the right.

The fundamental polygon of the projective plane.

The Möbius strip with a single edge, can be closed into a projective plane by gluing opposite open edges together.

In comparison the Klein bottle is a Möbius strip closed into a cylinder.

將怎樣闡釋必須用『齊次座標系』耶

Homogeneous coordinates

The points in the plane can be represented by homogeneous coordinates. A point has homogeneous coordinates [x : y : z], where the coordinates [x : y : z] and [tx : ty : tz] are considered to represent the same point, for all nonzero values of t. The points with coordinates [x : y : 1] are the usual real plane, called the finite part of the projective plane, and points with coordinates [x : y : 0], called points at infinity or ideal points, constitute a line called the line at infinity. (The homogeneous coordinates [0 : 0 : 0] do not represent any point.)

The lines in the plane can also be represented by homogeneous coordinates. A projective line corresponding to the plane ax + by + cz = 0 in R³ has the homogeneous coordinates (a : b : c). Thus, these coordinates have the equivalence relation (a : b : c) = (da : db : dc) for all nonzero values of d. Hence a different equation of the same line dax + dby + dcz = 0 gives the same homogeneous coordinates. A point [x : y : z] lies on a line (a : b : c) if ax + by + cz = 0. Therefore, lines with coordinates (a : b : c) where a, b are not both 0 correspond to the lines in the usual real plane, because they contain points that are not at infinity. The line with coordinates (0 : 0 : 1) is the line at infinity, since the only points on it are those with z = 0.

Points, lines, and planes

A line in P² can be represented by the equation ax + by + cz = 0. If we treat a, b, and c as the column vector ℓ and x, y, z as the column vector x then the equation above can be written in matrix form as:

x^Tℓ = 0 or ℓ^Tx = 0.

Using vector notation we may instead write

x ⋅ ℓ = 0 or ℓ ⋅ x = 0.

The equation k(x^Tℓ) = 0 (which k is a non-zero scalar) sweeps out a plane that goes through zero in R³ and k(x) sweeps out a line, again going through zero. The plane and line are linear subspaces in R³, which always go through zero.

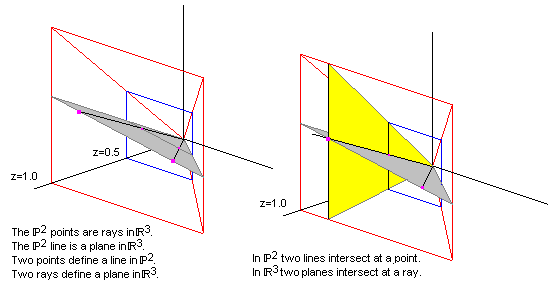
Ideal points

In P² the equation of a line is ax + by + c = 0 and this equation can represent a line on any plane parallel to the x, y plane by multiplying the equation by k.

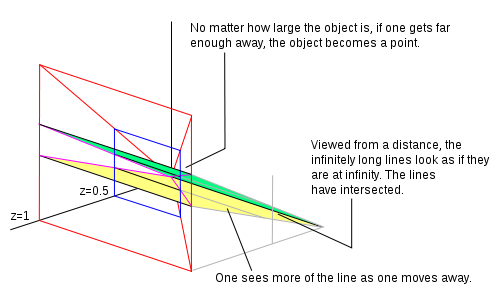
If z = 1 we have a normalized homogeneous coordinate. All points that have z = 1 create a plane. Let’s pretend we are looking at that plane (from a position further out along the z axis and looking back towards the origin) and there are two parallel lines drawn on the plane. From where we are standing (given our visual capabilities) we can see only so much of the plane, which we represent as the area outlined in red in the diagram. If we walk away from the plane along the z axis, (still looking backwards towards the origin), we can see more of the plane. In our field of view original points have moved. We can reflect this movement by dividing the homogeneous coordinate by a constant. In the adjacent image we have divided by 2 so the z value now becomes 0.5. If we walk far enough away what we are looking at becomes a point in the distance. As we walk away we see more and more of the parallel lines. The lines will meet at a line at infinity (a line that goes through zero on the plane at z = 0). Lines on the plane when z = 0 are ideal points. The plane at z = 0 is the line at infinity.

The homogeneous point (0, 0, 0) is where all the real points go when you’re looking at the plane from an infinite distance, a line on the z = 0 plane is where parallel lines intersect.

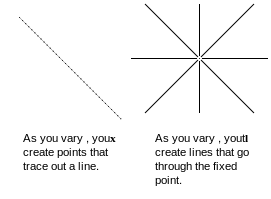
Duality

In the equation x^Tℓ = 0 there are two column vectors. You can keep either constant and vary the other. If we keep the point x constant and vary the coefficients ℓ we create new lines that go through the point. If we keep the coefficients constant and vary the points that satisfy the equation we create a line. We look upon x as a point, because the axes we are using are x, y, and z. If we instead plotted the coefficients using axis marked a, b, c points would become lines and lines would become points. If you prove something with the data plotted on axis marked x, y, and z the same argument can be used for the data plotted on axis marked a, b, and c. That is duality.

Lines joining points and intersection of lines (using duality)

The equation x^Tℓ = 0 calculates the inner product of two column vectors. The inner product of two vectors is zero if the vectors are orthogonal. In P², the line between the points x₁ and x₂ may be represented as a column vector ℓ that satisfies the equations x₁^Tℓ = 0 and x₂^Tℓ = 0, or in other words a column vector ℓ that is orthogonal to x₁ and x₂. The cross product will find such a vector: the line joining two points has homogeneous coordinates given by the equation x₁ × x₂. The intersection of two lines may be found in the same way, using duality, as the cross product of the vectors representing the lines, ℓ₁ × ℓ₂.

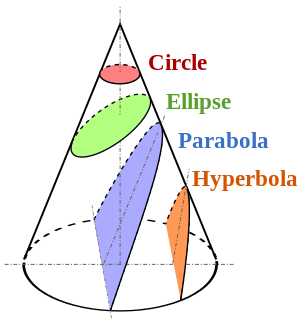
更別想當初也曾困惑『圓錐曲線』呀◎

當『博大精深』遇上『溫文婉約』是否『輾轉反側』？？

─── 摘自《紙張、鉛筆和橡皮擦》

話說那小汽車一時不見蹤影︰

影

影（又稱影子、背影），是一種物理現象，是光線被不透明物體阻檔而產生的黑暗範圍，與光源的方向相反。影的橫切面是二維輪廓 、阻檔光線物體的倒轉投影。影的大小、形狀隨光線的入射角而改變。

Shadows of visitors to the Eiffel Tower, viewed from the first platform

Shadow

A shadow is a dark area where light from a light source is blocked by an opaque object. It occupies all of the three-dimensional volume behind an object with light in front of it. The cross section of a shadow is a two-dimensional silhouette, or a reverse projection of the object blocking the light.

莫非它已進入怎麼收穫該怎麼栽耶？且精通

剪影

剪影（法語：silhouette）是一種將人事物以單色描繪（以黑色為主），凸顯輪廓的藝術圖像，或指剪影藝術本身，可屬一種視覺藝術，剪影被運用在各種方面。

The only known contemporary depiction of Martha Jefferson, wife of Thomas Jefferson.

之術乎？？還是它已深明『邏輯排中律』！

圖靈百年之後，『計算』並沒有變得更『簡單』，『爆炸』般的『知識』也沒使得『邏輯』推演更加『清晰』。或許那台『仙女計算機』並沒有『使用手冊』？還是她有使用手冊，祇可惜缺少那個伴隨著通過『圖靈測試』之『演算法』的呢？？

拉丁語 tertium non datur 聲稱︰

任何命題 必真。

這個叫做『排中律』的概念，有直覺主意的數學家反對，後來還成立了一個『數學建構主義』的流派。這不就是句『空話』的嗎？又何必需要反對？原因在於並非所有的概念都是可以，像『真假』、『是非』與『對錯』般的『二分』，在『黑白』之外不只有『灰』，甚至還有『色』。所以使用排中律一不小心就可能產生『虛假兩難論證』False dilemma。比方說有人論證想反駁『小三之歌』的『沒有拆不散的家庭，只有不努力的小三』︰

假使愛情堅定，無論如何考驗也不會改變；如果愛情不堅定，沒有小三也難長存。只有愛情堅定才會攜手建立家庭，所以再努力的小三也沒有用。

作者不知『堅不堅定』的兩極之間，果真該不該有『其他愛情』的存在？因此無法判斷這個論證對錯是否如此？？而『直覺邏輯者』卻認為應該取消排中律︰

平面上任何一條不自相交連續之『封閉曲線』，將平面分成『三』個區域，『 之外或 之內』之『二分』不包含著『 之中』，但它不是才是 的啊！！

，又得到『平行投影』之法呢？

Projection (linear algebra)

In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself such that P ² = P. That is, whenever P is applied twice to any value, it gives the same result as if it were applied once (idempotent). It leaves its image unchanged.^[1] Though abstract, this definition of “projection” formalizes and generalizes the idea of graphical projection. One can also consider the effect of a projection on a geometrical object by examining the effect of the projection on points in the object.

Simple example

Orthogonal projection

For example, the function which maps the point (x, y, z) in three-dimensional space R³ to the point (x, y, 0) is an orthogonal projection onto the x–y plane. This function is represented by the matrix

The action of this matrix on an arbitrary vector is

To see that P is indeed a projection, i.e., P = P², we compute

Oblique projection

A simple example of a non-orthogonal (oblique) projection (for definition see below) is

Via matrix multiplication, one sees that

proving that P is indeed a projection.

The projection P is orthogonal if and only if α = 0.

當此『順』『逆』之時，有無什麼文字︰

所以即使『一根針』落下時，都一定會『碰到天使』，……，進而再『申論』了『天使』的『大與小』，那『小者之小 』在『針尖 』上能『立』『成千上萬』個『小天使』── 此『玄論功夫』果真是『匪夷所思』的吧！！

─── 摘自《W!o+ 的《小伶鼬工坊演義》︰ 一窺全豹之系統設計《破繭》》

雖有強大運算能力，卻不知追求什麼目標，此乃小汽車之迷惘也。左看

Anaglyph 3D

Anaglyph 3D is the name given to the stereoscopic 3D effect achieved by means of encoding each eye’s image using filters of different (usually chromatically opposite) colors, typically red and cyan. Anaglyph 3D images contain two differently filtered colored images, one for each eye. When viewed through the “color-coded” “anaglyph glasses”, each of the two images reaches the eye it’s intended for, revealing an integrated stereoscopic image. The visual cortex of the brain fuses this into the perception of a three-dimensional scene or composition.

Anaglyph images have seen a recent resurgence due to the presentation of images and video on the Web, Blu-ray Discs, CDs, and even in print. Low cost paper frames or plastic-framed glasses hold accurate color filters that typically, after 2002, make use of all 3 primary colors. The current norm is red and cyan, with red being used for the left channel. The cheaper filter material used in the monochromatic past dictated red and blue for convenience and cost. There is a material improvement of full color images, with the cyan filter, especially for accurate skin tones.

Video games, theatrical films, and DVDs can be shown in the anaglyph 3D process. Practical images, for science or design, where depth perception is useful, include the presentation of full scale and microscopic stereographic images. Examples from NASA include Mars Rover imaging, and the solar investigation, called STEREO, which uses two orbital vehicles to obtain the 3D images of the sun. Other applications include geological illustrations by the United States Geological Survey, and various online museum objects. A recent application is for stereo imaging of the heart using 3D ultra-sound with plastic red/cyan glasses.

Anaglyph images are much easier to view than either parallel (diverging) or crossed-view pairs stereograms. However, these side-by-side types offer bright and accurate color rendering, not easily achieved with anaglyphs. Recently, cross-view prismatic glasses with adjustable masking have appeared, that offer a wider image on the new HD video and computer monitors. Template:3D Glasses

Stereoscopic effect used in macro photography 3D red cyan glasses are recommended to view this image correctly.

Types

Complementary color

Paper anaglyph filters produce an acceptable image at low cost and are suitable for inclusion in magazines.

Complementary color anaglyphs employ one of a pair of complementary color filters for each eye. The most common color filters used are red and cyan. Employing tristimulus theory, the eye is sensitive to three primary colors, red, green, and blue. The red filter admits only red, while the cyan filter blocks red, passing blue and green (the combination of blue and green is perceived as cyan). If a paper viewer containing red and cyan filters is folded so that light passes through both, the image will appear black. Another recently introduced form employs blue and yellow filters. (Yellow is the color perceived when both red and green light passes through the filter.)

Anaglyph images have seen a recent resurgence because of the presentation of images on the Internet. Where traditionally, this has been a largely black & white format, recent digital camera and processing advances have brought very acceptable color images to the internet and DVD field. With the online availability of low cost paper glasses with improved red-cyan filters, and plastic framed glasses of increasing quality, the field of 3D imaging is growing quickly. Scientific images where depth perception is useful include, for instance, the presentation of complex multi-dimensional data sets and stereographic images of the surface of Mars. With the recent release of 3D DVDs, they are more commonly being used for entertainment. Anaglyph images are much easier to view than either parallel sighting or crossed eye stereograms, although these types do offer more bright and accurate color rendering, most particularly in the red component, which is commonly muted or desaturated with even the best color anaglyphs. A compensating technique, commonly known as Anachrome, uses a slightly more transparent cyan filter in the patented glasses associated with the technique. Processing reconfigures the typical anaglyph image to have less parallax to obtain a more useful image when viewed without filters.

Piero della Francesca, Ideal City in an Anaglyph version 3D red cyan glasses are recommended to view this image correctly.

右瞧

Polarized 3D system

A polarized 3D system uses polarization glasses to create the illusion of three-dimensional images by restricting the light that reaches each eye (an example of stereoscopy).

To present stereoscopic images and films, two images are projected superimposed onto the same screen or display through different polarizing filters. The viewer wears low-cost eyeglasses which contain a pair of different polarizing filters. As each filter passes only that light which is similarly polarized and blocks the light polarized in the opposite direction, each eye sees a different image. This is used to produce a three-dimensional effect by projecting the same scene into both eyes, but depicted from slightly different perspectives. Multiple people can view the stereoscopic images at the same time.

Circularly polarized 3D glasses in front of an LCD tablet with a quarter-wave retarder on top of it; the λ/4 plate at 45° produces a definite handedness, which is transmitted by the left filter but blocked by the right filter.

System construction and examples

Polarized light reflected from an ordinary motion picture screen typically loses most of its polarization, but the loss is negligible if a silver screen or aluminized screen is used. This means that a pair of aligned DLP projectors, some polarizing filters, a silver screen, and a computer with a dual-head graphics card can be used to form a relatively high-cost (over US$10,000 in 2010) system for displaying stereoscopic 3D data simultaneously to a group of people wearing polarized glasses.^{[citation needed]}

In the case of RealD a circularly polarizing liquid crystal filter which can switch polarity 144 times per second^[2] is placed in front of the projector lens. Only one projector is needed, as the left and right eye images are displayed alternately. Sony features a new system called RealD XLS, which shows both circularly polarized images simultaneously: A single 4K projector displays two 2K images one above the other, a special lens attachment polarizes and projects the images on top of each other.^[3]

Optical attachments can be added to traditional 35 mm projectors to adapt them for projecting film in the “over-and-under” format, in which each pair of images is stacked within one frame of film. The two images are projected through different polarizers and superimposed on the screen. This is a very cost-effective way to convert a theater for 3-D as all that is needed are the attachments and a non-depolarizing screen surface, rather than a conversion to digital 3-D projection. Thomson Technicolor currently produces an adapter of this type.^[4]

When stereo images are to be presented to a single user, it is practical to construct an image combiner, using partially silvered mirrors and two image screens at right angles to one another. One image is seen directly through the angled mirror whilst the other is seen as a reflection. Polarized filters are attached to the image screens and appropriately angled filters are worn as glasses. A similar technique uses a single screen with an inverted upper image, viewed in a horizontal partial reflector, with an upright image presented below the reflector, again with appropriate polarizers.^{[original research?]}

Functional principle of polarized 3D systems

※ 註

SVEN: Stereoscopic Visualization ENvironment

In the Math, Computer Science, and Physics Department at Wartburg College, we have been developing techniques for stereoscopic visualization/virtual reality using readily available, commodity hardware and highly-accessible software. Our goal is to make this technology feasible in virtually any classroom setting. This page contains links to some materials related to the project. Comments or questions should be directed to John Zelle or Charles Figura.

Overview Materials

Paper: Simple, Low-Cost Stereographics: VR for Everyone

Paper accepted for SIGCSE 2004. This paper is a general HOWTO for stereographic visualization in the classroom. It explains both the hardware and software that we are using for 3D visualizations.

Presentation: Simple, Low-Cost Stereographics: VR for Everyone

This is the HTML version of the presentation of the above paper at SIGCSE 2004. Sigcse04-slides.pdf is a PDF version of the slides, and sigcse04-handout.pdf contains these slides 4 to a page.

Presentation: Classroom Virtual Reality: Simple, Affordable Stereoscopic Visualization

HTML version of presentation at American Association of Physics Teachers, Winter 2004. This presentation includes a basic outline of our approach and some example applications in Physics.

都是『雙眼』所作『事』耶？『單眼』將如何乎？？

傳說有一天偶見『顫抖』的『藍日』︰

Wiggle stereoscopy

Wiggle stereoscopy is an example of stereoscopy in which left and right images of a stereogram are animated. This technique is also called wiggle 3-D or wobble 3-D, sometimes also Piku-Piku (Japanese for “twitching”).^[1]

The sense of depth from such images is due to parallax and to changes to the occlusion of background objects. In contrast to other stereo display techniques, the same image is presented to both eyes. Animation can be done in a web browser with an animated GIF image, Flash animation, or JavaScript program.

A wiggle stereogram of the Sun alternating between left and right eye images taken by the NASA‘s STEREO solar observation mission

大喊『尤里卡』Eureka 後！不知所蹤☆

Kinetic depth effect

In visual perception, the kinetic depth effect refers to the phenomenon whereby the three-dimensional structural form of an object can be perceived when the object is moving. In the absence of other visual depth cues, this might be the only perception mechanism available to infer the object’s shape. Being able to identify a structure from a motion stimulus through the human visual system was shown by Wallach and O’Connell in the 1950s through their experiments.^[1]

For example, if a shadow is cast onto a screen by a rotating wire shape, a viewer can readily perceive the shape of the structure behind the screen from the motion and deformation of the shadow.

There are two propositions as to how three-dimensional images are perceived. The experience of three-dimensional images can be caused by differences in the pattern of stimulation on the retina, in comparison to two-dimensional images. Gestalt psychologists hold the view that rules of organization must exist in accordance to the retinal projections of three-dimensional forms which happen to form three-dimensional percepts. Most retinal images of two-dimensional forms lead to two-dimensional forms in experience as well. The other deduction is related to previous experience. Unfortunately, this assumption does not explain how past experience influences perception of images.^[2]

In order to model the calculation of depth values from relative movement, many efforts have been made to infer these values using other information like geometry and measurements of objects and their positions.^[3] This is related to the extraction of structure from motion in computer vision. In addition, an individual’s ability to realize the kinetic depth effect conclusively shows that the visual system can independently figure the structure from motion problem.^[4]

As with other depth cues, the kinetic depth effect is almost always produced in combination with other effects, most notably the motion parallax effect. For instance, the rotating circles illusion^[5] and the rotating dots visualization^[6] (which is similar in principle to the projected wireframe demonstration mentioned above) rely strongly on the previous knowledge that objects (or parts thereof) further from the observer appear to move more slowly than those that are closer.

The kinetic depth effect can manifest independently, however, even when motion parallax is not present. An example of such a situation is the art installment “The Analysis of Beauty”,^[7] by the Disinformation project, created as a tribute to William Hogarth‘s concept of the Serpentine Line (which was presented in his homonymous book).

The Spinning Dancer is a kinetic, bistable optical illusion resembling a pirouetting female dancer. Some observers initially see the figure as spinning clockwise and some anticlockwise. Additionally, some may see the figure suddenly spin in the opposite direction. The illusion derives from an inherent ambiguity from the lack of visual cues for depth. There are other optical illusions that originate from the same or similar kind of visual ambiguity, such as the Necker cube. If you focus on one part of her body, such as her foot and the shadow, it is possible to switch back and forth by focusing on the opposite motion that she is currently performing with her foot. When trying to switch from clockwise to counterclockwise wise I have found focusing on the shadow of her foot for a couple seconds allows you to see the opposite direction. And in some cases when able to switch back and forth with ease it looks like she is waving her leg back and forth and has lost the spinning effect entirely. .