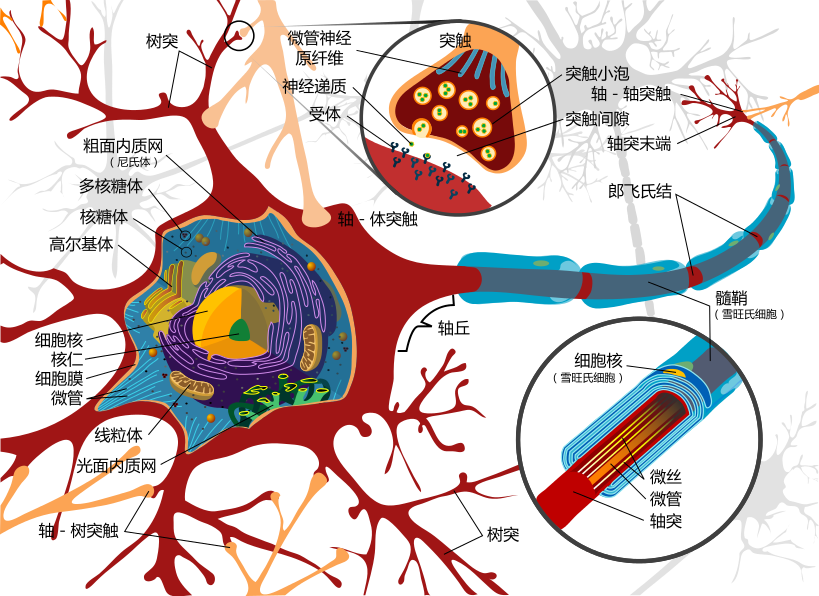
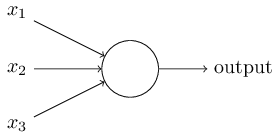
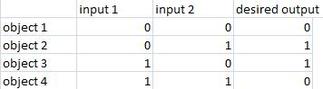
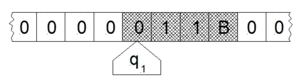
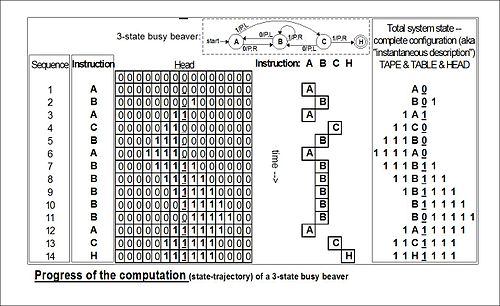
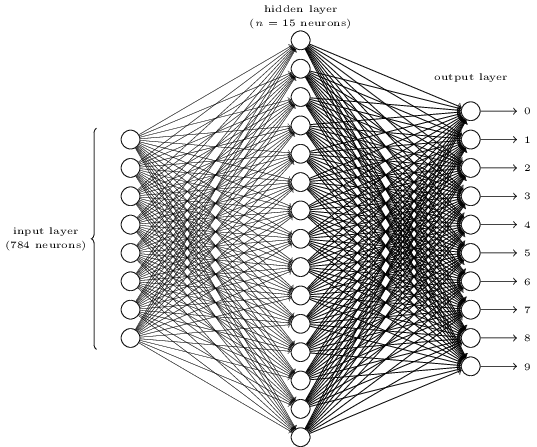
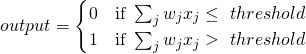W!o+ 的《小伶鼬工坊演義》︰神經網絡【Perceptron】四

2016-04-10 懸鉤子

一九四九年加拿大心理學家唐納德‧赫布 Donald Hebb ── 被譽為神經心理學與神經網絡之父 ── 寫了一本

大作，提出了『學習』之『神經基礎』，今稱之為『赫布假定』 Hebb’s postulate 。這個『赫布理論』維基百科詞條這麼說︰

Hebbian theory

Hebbian theory is a theory in neuroscience that proposes an explanation for the adaptation of neurons in the brain during the learning process. It describes a basic mechanism for synaptic plasticity, where an increase in synaptic efficacy arises from the presynaptic cell’s repeated and persistent stimulation of the postsynaptic cell. Introduced by Donald Hebb in his 1949 book The Organization of Behavior,^[1] the theory is also called Hebb’s rule, Hebb’s postulate, and cell assembly theory. Hebb states it as follows:

Let us assume that the persistence or repetition of a reverberatory activity (or “trace”) tends to induce lasting cellular changes that add to its stability.… When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A‘s efficiency, as one of the cells firing B, is increased.^[1]

The theory is often summarized by Siegrid Löwel’s phrase: “Cells that fire together, wire together.” ^[2] However, this summary should not be taken literally. Hebb emphasized that cell A needs to “take part in firing” cell B, and such causality can only occur if cell A fires just before, not at the same time as, cell B. This important aspect of causation in Hebb’s work foreshadowed what is now known about spike-timing-dependent plasticity, which requires temporal precedence.^[3] The theory attempts to explain associative or Hebbian learning, in which simultaneous activation of cells leads to pronounced increases in synaptic strength between those cells, and provides a biological basis for errorless learning methods for education and memory rehabilitation.

……

Principles

From the point of view of artificial neurons and artificial neural networks, Hebb’s principle can be described as a method of determining how to alter the weights between model neurons. The weight between two neurons increases if the two neurons activate simultaneously, and reduces if they activate separately. Nodes that tend to be either both positive or both negative at the same time have strong positive weights, while those that tend to be opposite have strong negative weights.

The following is a formulaic description of Hebbian learning: (note that many other descriptions are possible)

\,w_{ij}=x_ix_j

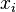where $w_{ij}$ is the weight of the connection from neuron $j$ to neuron $i$ and $x_i$ the input for neuron $i$ . Note that this is pattern learning (weights updated after every training example). In a Hopfield network, connections $w_{ij}$ are set to zero if $i=j$ (no reflexive connections allowed). With binary neurons (activations either 0 or 1), connections would be set to 1 if the connected neurons have the same activation for a pattern.

Another formulaic description is:

w_{ij} = \frac{1}{p} \sum_{k=1}^p x_i^k x_j^k,\,

where $w_{ij}$ is the weight of the connection from neuron $j$ to neuron $i$ , $p$ is the number of training patterns, and $x_{i}^k$ the $k$ th input for neuron $i$ . This is learning by epoch (weights updated after all the training examples are presented). Again, in a Hopfield network, connections $w_{ij}$ are set to zero if $i=j$ (no reflexive connections).

A variation of Hebbian learning that takes into account phenomena such as blocking and many other neural learning phenomena is the mathematical model of Harry Klopf.^{[citation needed]} Klopf’s model reproduces a great many biological phenomena, and is also simple to implement.

Generalization and stability

Hebb’s Rule is often generalized as

\,\Delta w_i = \eta x_i y,

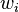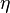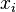or the change in the $i$ th synaptic weight $w_i$ is equal to a learning rate $\eta$ times the $i$ th input $x_i$ times the postsynaptic response $y$ . Often cited is the case of a linear neuron,

\,y = \sum_j w_j x_j,

and the previous section’s simplification takes both the learning rate and the input weights to be 1. This version of the rule is clearly unstable, as in any network with a dominant signal the synaptic weights will increase or decrease exponentially. However, it can be shown that for any neuron model, Hebb’s rule is unstable.^[5] Therefore, network models of neurons usually employ other learning theories such as BCM theory, Oja’s rule,^[6] or the Generalized Hebbian Algorithm.

───

如果『赫布規則』可以證明是『unstable』不穩定，那麼重提它有什麼意義嗎？或許意義在於這是『開創者』經常遭遇的『狀況』，而『後繼者』往往可因增補而受益。故而提及於此，使得讀者可以比較其與

《W!o+ 的《小伶鼬工坊演義》︰神經網絡【Perceptron】二》

文本裡之『感知器』的『學習規則』之異同︰

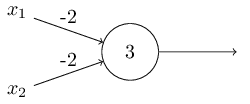
The Perceptron

The next major advance was the perceptron, introduced by Frank Rosenblatt in his 1958 paper. The perceptron had the following differences from the McCullough-Pitts neuron:

The weights and thresholds were not all identical.
Weights can be positive or negative.
There is no absolute inhibitory synapse.
Although the neurons were still two-state, the output function f(u) goes from [-1,1], not [0,1]. (This is no big deal, as a suitable change in the threshold lets you transform from one convention to the other.)
Most importantly, there was a learning rule.

Describing this in a slightly more modern and conventional notation (and with V_i = [0,1]) we could describe the perceptron like this:

This shows a perceptron unit, i, receiving various inputs I_j, weighted by a “synaptic weight” W_ij.

The ith perceptron receives its input from n input units, which do nothing but pass on the input from the outside world. The output of the perceptron is a step function:

and

For the input units, V_j = I_j. There are various ways of implementing the threshold, or bias, theta_i. Sometimes it is subtracted, instead of added to the input u, and sometimes it is included in the definition of f(u).

A network of two perceptrons with three inputs would look like:

Note that they don’t interact with each other – they receive inputs only from the outside. We call this a “single layer perceptron network” because the input units don’t really count. They exist just to provide an output that is equal to the external input to the net.

The learning scheme is very simple. Let t_i be the desired “target” output for a given input pattern, and V_i be the actual output. The error (called “delta”) is the difference between the desired and the actual output, and the change in the weight is chosen to be proportional to delta.

Specifically, and

where is the learning rate.

Can you see why this is reasonable? Note that if the output of the ith neuron is too small, the weights of all its inputs are changed to increase its total input. Likewise, if the output is too large, the weights are changed to decrease the total input. We’ll better understand the details of why this works when we take up back propagation. First, an example.

……

如是看來『關鍵差異』就落在表達式的了？？過去已『學會』的 $t_i = V_i$ 應該『保持』原態；尚未能『學會』的需要『將來』得減少『誤差』的吧！！

若問什麼阻礙『新觀念』的理解？什麼導致『詮釋』的誤解？？又有什麼造成用『不同概念』來『表達』的困難？？？誠難以回答也！或許『學會了』意味『概念』之牢固！！曾經多次『重複』訴說很難被『改變』之耶！！！

只能邀請讀者看看與想想之前文本

如果有一個人依照波利亞 Pólya 的思考方法去『了解問題』，

【問題】
有一個農民到集市買了一隻狐狸、一隻鵝和一袋豆子，回家時要渡過一條河。河中有一條船，但是只能裝一樣東西。而且，如果沒有人看管，狐狸會吃掉鵝，而鵝又很喜歡吃豆子。問：怎樣才能讓這些東西都安全過河？

甚至這個人還能將此問題作語文的翻譯︰

《 Fox, goose and bag of beans puzzle 》

Once upon a time a farmer went to market and purchased a fox, a goose, and a bag of beans. On his way home, the farmer came to the bank of a river and rented a boat. But in crossing the river by boat, the farmer could carry only himself and a single one of his purchases – the fox, the goose, or the bag of beans.

If left together, the fox would eat the goose, or the goose would eat the beans.

The farmer’s challenge was to carry himself and his purchases to the far bank of the river, leaving each purchase intact. How did he do it?

假使有人問此人如何求解這個問題，他還能毫不猶豫的說出答案與推導過程︰

【解答】

第一步、帶鵝過河；
第二步、空手回來；
第三步、帶狐狸〔或豆子〕過河；
第四步、帶鵝回來；
第五步、帶豆子〔或狐狸〕過河；
第六步、空手回來；
第七步、帶鵝過河。

然而他也許未必可以用 pyDatalog 語言來作『表達』！這卻又是『為什麼』的呢？難道說，波利亞的方法不管用，或是我們並不『明白』它的用法，還是我們尚且不『了解』 pyDatalog 語言，以至於無法『思考』那個『表達』之法的哩？？

如果此時我們想想那位『塞萬提斯』用長篇小說來『反騎士』，卻被『讀』成了擁有『阿 Q 精神』的『夢幻騎士』，也許該讚揚那些為『受壓迫』者發聲之人吧！或許須細思『非理性』和『不理性』概念之差別的吖！！

……

，你將會發現這個無形的『字詞網絡』框住了人們的『思維』，此正所以換個『概念體系』常常會覺得寸步難行的吧？！故而所謂的『改寫重述』多半得是『跳脫框架』的『創造性』活動。最後就讓我們歸結到俗話所講︰一圖勝千言的耶！？

【邏輯網】

───摘自《勇闖新世界︰《 pyDatalog 》導引《十》豆鵝狐人之改寫篇》

之所以言難盡意乎？？？

樹莓派、樹莓派之學習、樹莓派之教育

W!o+ 的《小伶鼬工坊演義》︰神經網絡【Perceptron】三

2016-04-09 懸鉤子

為什麼人們會在意『感知器』 XOR 的問題呢？如果一個『神經元』就是一台『圖靈機』，或足以表達造物之神奇！或可以顯現人所以成萬物之靈的理據？還是只是對

感知器

感知器（英語：Perceptron）是Frank Rosenblatt在1957年就職於Cornell航空實驗室（Cornell Aeronautical Laboratory）時所發明的一種人工神經網路。它可以被視為一種最簡單形式的前饋神經網路，是一種二元線性分類器。

Frank Rosenblatt給出了相應的感知機學習算法，常用的有感知機學習、最小二乘法和梯度下降法。譬如，感知機利用梯度下降法對損失函數進行極小化，求出可將訓練數據進行線性劃分的分離超平面，從而求得感知機模型。

感知機是生物神經細胞的簡單抽象。神經細胞結構大致可分為：樹突、突觸、細胞體及軸突。單個神經細胞可被視為一種只有兩種狀態的機器——激動時為『是』，而未激動時為『否』。神經細胞的狀態取決於從其它的神經細胞收到的輸入信號量，及突觸的強度（抑制或加強）。當信號量總和超過了某個閾值時，細胞體就會激動，產生電脈衝。電脈衝沿著軸突並通過突觸傳遞到其它神經元。為了模擬神經細胞行為，與之對應的感知機基礎概念被提出，如權量（突觸）、偏置（閾值）及激活函數（細胞體）。

在人工神經網絡領域中，感知機也被指為單層的人工神經網絡，以區別於較複雜的多層感知機（Multilayer Perceptron）。作為一種線性分類器，（單層）感知機可說是最簡單的前向人工神經網絡形式。儘管結構簡單，感知機能夠學習並解決相當複雜的問題。感知機主要的本質缺陷是它不能處理線性不可分問題。

神經細胞結構示意圖

歷史

1943年，心理學家Warren McCulloch和數理邏輯學家Walter Pitts在合作的《A logical calculus of the ideas immanent in nervous activity》^[1]論文中提出並給出了人工神經網絡的概念及人工神經元的數學模型，從而開創了人工神經網絡研究的時代。1949年，心理學家唐納德·赫布在《The Organization of Behavior》^[2]論文中描述了神經元學習法則。

人工神經網絡更進一步被美國神經學家Frank Rosenblatt所發展。他提出了可以模擬人類感知能力的機器，並稱之為『感知機』。1957年，在Cornell航空實驗室中，他成功在IBM 704機上完成了感知機的仿真。兩年後，他又成功實現了能夠識別一些英文字母、基於感知機的神經計算機——Mark1，並於1960年6月23日，展示與眾。

為了『教導』感知機識別圖像，Rosenblatt，在Hebb學習法則的基礎上，發展了一種疊代、試錯、類似於人類學習過程的學習算法——感知機學習。除了能夠識別出現較多次的字母，感知機也能對不同書寫方式的字母圖像進行概括和歸納。但是，由於本身的局限，感知機除了那些包含在訓練集裡的圖像以外，不能對受干擾（半遮蔽、不同大小、平移、旋轉）的字母圖像進行可靠的識別。

首個有關感知機的成果，由Rosenblatt於1958年發表在《The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain》^[3]的文章里。1962年，他又出版了《Principles of Neurodynamics: Perceptrons and the theory of brain mechanisms》^[4]一書，向大眾深入解釋感知機的理論知識及背景假設。此書介紹了一些重要的概念及定理證明，例如感知機收斂定理。

雖然最初被認為有著良好的發展潛能，但感知機最終被證明不能處理諸多的模式識別問題。1969年，Marvin Minsky和Seymour Papert在《Perceptrons》書中，仔細分析了以感知機為代表的單層神經網絡系統的功能及局限，證明感知機不能解決簡單的異或（XOR）等線性不可分問題，但Rosenblatt和Minsky及Papert等人在當時已經了解到多層神經網絡能夠解決線性不可分的問題。

由於Rosenblatt等人沒能夠及時推廣感知機學習算法到多層神經網絡上，又由於《Perceptrons》在研究領域中的巨大影響，及人們對書中論點的誤解，造成了人工神經領域發展的長年停滯及低潮，直到人們認識到多層感知機沒有單層感知機固有的缺陷及反向傳播算法在80年代的提出，才有所恢復。1987年，書中的錯誤得到了校正，並更名再版為《Perceptrons – Expanded Edition》。

近年，在Freund及Schapire（1998）使用核技巧改進感知機學習算法之後，愈來愈多的人對感知機學習算法產生興趣。後來的研究表明除了二元分類，感知機也能應用在較複雜、被稱為structured learning類型的任務上（Collins, 2002），又或使用在分布式計算環境中的大規模機器學習問題上（McDonald, Hall and Mann, 2011）。

───

美麗的誤解？！要是『感知器網絡』能夠學習成為『豆鵝狐人』

『豆鵝狐人』之問題就是

《狐狸、鵝、豆子問題》
狐狸、鵝、豆子問題〔又稱狼、羊、菜問題〕是一則古老的智力遊戲題。

【解答】

在此『問』的『問題』是︰

如何將之用 pyDatalog 語言『改寫重述』，使得可以用『程式』來執行『推理』，得到『答案』的呢？

─── 摘自《勇闖新世界︰《 pyDatalog 》導引《十》豆鵝狐人之問題篇》

之『解題者』！！那麼它的『命題推理』能力

『命題邏輯』 Propositional calculus 是一種『真、假』二值邏輯。在這個邏輯體系裡，所有命題『非真即假』。它的主要特徵可由『矛盾蘊函萬有』，叫做『爆炸原理』，來概括︰

一、假設甲與非甲皆真【矛盾】

二、甲真【來自於一之中『與』 and 的詞義】

三、甲或萬有為真【來自於二以及『或』 or 的詞義】

四、非甲【來自於一之中『與』 and 的詞義】

五、萬有【來自於三和四，理則歸結】

所以證明了『矛盾 → 萬有』為真。

或許可以說近代『邏輯』相關的零零種種研究，多半與一個稱之為『羅素悖論』︰

有一位理髮師宣稱，他為所有不為自己理髮的人理髮，請問他為不為自己理髮？ ── 引自《{x|x ∉ x} ！！？？》──

者有千絲萬縷的聯繫！同一篇文章中所講到的︰邏輯學家為了說明邏輯推導是否合理、有效和合法，構造了『真值表』︰

P ，非 P P ， ~P	Q	P 且 Q P ‧ Q	P 或 Q P + Q	若 P 則 Q P → Q	非 P 或 Q ~P + Q
真，假 T F	真 T	真 T	真 T	真 T	真 T
真，假 T F	假 F	假 F	真 T	假 F	假 F
假，真 F T	真 T	假 F	真 T	真 T	真 T
假，假 F F	假 F	假 F	假 F	真 T	真 T

。真值表考慮了陳述句所有的真假可能狀況，如果兩個陳述句 ── 比方說 P → Q 和 ~P + Q ──，在每一種狀況裡都真假相同，那麼他們在邏輯上表示同樣的陳述，只不過穿著不同說法的外衣 。假使有一個陳述句在所有的真假可能狀況裡頭都是真的，這稱之為『恆真句』，舉例說 P + ~P。恆真句構成了論述合理有效推論的基礎。就讓我們說說有名的『三段論』吧︰

若 P 則 Q
因 P
故 Q

，把這個推理改寫成 ((P→Q)‧P)→Q ，那它將是個恆真句。雖然『 P 或非 P 』是個恆真句，但是彷彿像句空話，什麼也沒有說，事實上它說︰凡是陳述非真即假，假使 P 是真的，那麼非 P 一定是假的。這就是大名鼎鼎的『矛盾律』！可是那要怎麼看『明天可能會下雨』或『明天可能不會下雨』呢？好似『想非想非非想』一般，邏輯學的路途依然遙遠！！

，這個『真值表』詮釋，也就是『數理邏輯』中『埃爾布朗解釋』Herbrand interpretation ，紀念英年早逝的『雅克‧埃爾布朗』 Jacques Herbrand 對『機器證明』基礎之貢獻︰

In mathematical logic, a Herbrand interpretation is an interpretation in which all constants and function symbols are assigned very simple meanings. Specifically, every constant is interpreted as itself, and every function symbol is interpreted as the function that applies it. The interpretation also defines predicate symbols as denoting a subset of the relevant Herbrand base, effectively specifying which ground atoms are true in the interpretation. This allows the symbols in a set of clauses to be interpreted in a purely syntactic way, separated from any real instantiation.

The importance of Herbrand interpretations is that, if any interpretation satisfies a given set of clauses S then there is a Herbrand interpretation that satisfies them. Moreover, Herbrand’s theorem states that if S is unsatisfiable then there is a finite unsatisfiable set of ground instances from the Herbrand universe defined by S. Since this set is finite, its unsatisfiability can be verified in finite time. However there may be an infinite number of such sets to check.

It is named after Jacques Herbrand.

如此所謂『原子』 atom ，或說『邏輯原子』，意指『真假陳述』的『最小單元』，其內沒有其它的『邏輯結構』之『基本命題』。如是所謂『子句』 clause 就是有特定『邏輯結構』的『命題』︰

$H_1 \ or \ H_2 \cdots \ or \ H_m \ <= \ T_1 \ and \ T_2 \cdots \ and \ T_n$

。由於『邏輯運算符號』彼此間的『邏輯等價』性，使得我們可以選擇『機器證明』的合適『句式』，在盡可能不失去『一般性』的狀況下建構該程式語言。也可以說『特定性』是『實務』考量下的結果。因此我們可以明白『霍恩子句』 Horn clause ︰

A Horn clause is a clause (a disjunction of literals) with at most one positive, i.e. unnegated, literal.

Conversely, a disjunction of literals with at most one negated literal is called a dual-Horn clause.

A Horn clause with exactly one positive literal is a definite clause; a definite clause with no negative literals is sometimes called a fact; and a Horn clause without a positive literal is sometimes called a goal clause (note that the empty clause consisting of no literals is a goal clause). These three kinds of Horn clauses are illustrated in the following propositional example:

	Disjunction form	Implication form	Read intuitively as
Definite clause	¬p ∨ ¬q ∨ … ∨ ¬t ∨ u	u ← p ∧ q ∧ … ∧ t	assume that, if p and q and … and t all hold, then also u holds
Fact	u	u	assume that u holds
Goal clause	¬p ∨ ¬q ∨ … ∨ ¬t	false ← p ∧ q ∧ … ∧ t	show that p and q and … and t all hold ^{[note 1]}

In the non-propositional case, all variables in a clause are implicitly universally quantified with scope the entire clause. Thus, for example:

¬ human(X) ∨ mortal(X)

stands for:

∀X( ¬ human(X) ∨ mortal(X) )

which is logically equivalent to:

∀X ( human(X) → mortal(X) )

Horn clauses play a basic role in constructive logic and computational logic. They are important in automated theorem proving by first-order resolution, because the resolvent of two Horn clauses is itself a Horn clause, and the resolvent of a goal clause and a definite clause is a goal clause. These properties of Horn clauses can lead to greater efficiencies in proving a theorem (represented as the negation of a goal clause).

Propositional Horn clauses are also of interest in computational complexity, where the problem of finding truth value assignments to make a conjunction of propositional Horn clauses true is a P-complete problem (in fact solvable in linear time), sometimes called HORNSAT. (The unrestricted Boolean satisfiability problem is an NP-complete problem however.) Satisfiability of first-order Horn clauses is undecidable.

的由來，它的『重要性』以及可能的『限制性』。進而理解『證明理論』 Proof Theory 所講的『 resolution 』邏輯推導歸結與『unification』變元替換一致化。且清楚明白『歸謬證法』 proof by refutation 在『證明理論』中的主導地位。

─── 摘自《勇闖新世界︰《 pyDatalog 》導引《三》》

果真不能『自知』︰一個『感知器』不足以解決『XOR』問題？？因為如果假設可以，依據 XOR 的 $(x_1,x_2)$ 真值表定義

[ $(1,1) \longrightarrow 0$ ]

$w_1 \cdot 1 + w_2 \cdot 1 - b \leq 0$

[ $(0,0) \longrightarrow 0$ ]

$-b \leq 0$

[ $(1,0) \longrightarrow 1$ ]

$w_1 \cdot 1 - b > 0$

[ $(0,1) \longrightarrow 1$ ]

$w_2 \cdot 1 - b > 0$

所以 $b \geq 0 , \ w_1 > b. \ w_2 > b$

但這與 $w_1 + w_2 \leq b$ 卻矛盾！！

由是當知，切莫輕忽對待任何『基楚概念』。即使『感知器』

Perceptrons

What is a neural network? To get started, I’ll explain a type of artificial neuron called a perceptron. Perceptrons were developed in the 1950s and 1960s by the scientist Frank Rosenblatt, inspired by earlier work by Warren McCulloch and Walter Pitts. Today, it’s more common to use other models of artificial neurons – in this book, and in much modern work on neural networks, the main neuron model used is one called the sigmoid neuron. We’ll get to sigmoid neurons shortly. But to understand why sigmoid neurons are defined the way they are, it’s worth taking the time to first understand perceptrons.

So how do perceptrons work? A perceptron takes several binary inputs, $x_1, x_2, \cdots$ $x_{1}, x_{2}, \dots$ , and produces a single binary output:

In the example shown the perceptron has three inputs, $x_1, x_2, x_3$

x_{1}, x_{2}, x_{3}

. In general it could have more or fewer inputs. Rosenblatt proposed a simple rule to compute the output. He introduced weights, $w_1,w_2,\cdots$

w_{1}, w_{2}, \dots

, real numbers expressing the importance of the respective inputs to the output. The neuron’s output,

0

1

, is determined by whether the weighted sum $\sum_j w_j x_j$

\sum_{j} w_{j} x_{j}

is less than or greater than some threshold value. Just like the weights, the threshold is a real number which is a parameter of the neuron. To put it in more precise algebraic terms:

output = \begin{cases}0 & \text{if } \sum_j w_j x_j \leq \ threshold\\1 & \text{if} \ \sum_j w_j x_j > \ threshold\end{cases}

That’s all there is to how a perceptron works!

……

之定義看似『簡單』，它的『數理』邏輯歸結未必可『一眼望盡』，囫圇吞棗者恐有『見樹不見林』之失耶！！

樹莓派、樹莓派之學習、樹莓派之教育

W!o+ 的《小伶鼬工坊演義》︰神經網絡【Perceptron】二

2016-04-08 懸鉤子

據知一九四三年 Warren McCullogh 和 Walter Pitts 因為生物

神經元

神經元（neuron），又名神經原或神經細胞（nerve cell），是神經系統的結構與功能單位之一。神經元佔了神經系統約10%，其他大部分由膠狀細胞所構成。基本構造由樹突、軸突、髓鞘、細胞核組成。傳遞形成電流，在其尾端為受體，藉由化學物質傳導(多巴胺、乙醯膽鹼)，在適當的量傳遞後在兩個突觸間形成電流傳導。

人腦中，神經細胞約有860億個。其中約有700億個為小腦顆粒細胞（cerebellar granule cell）

220px-PurkinjeCell

1899年科學家所畫神經元的圖

之啟發，創造了今天稱之為『McCulloch–Pitts (MCP) neuron』的『人工神經元』數學模型︰

Some specific models of artificial neural nets

McCullogh-Pitts Model

In 1943 two electrical engineers, Warren McCullogh and Walter Pitts, published the first paper describing what we would call a neural network. Their “neurons” operated under the following assumptions:

They are binary devices (V_i = [0,1])
Each neuron has a fixed threshold, theta
The neuron receives inputs from excitatory synapses, all having identical weights. (However it my receive multiple inputs from the same source, so the excitatory weights are effectively positive integers.)
Inhibitory inputs have an absolute veto power over any excitatory inputs.
At each time step the neurons are simultaneously (synchronously) updated by summing the weighted excitatory inputs and setting the output (V_i) to 1 iff the sum is greater than or equal to the threhold AND if the neuron receives no inhibitory input.

We can summarize these rules with the McCullough-Pitts output rule

and the diagram

Using this scheme we can figure out how to implement any Boolean logic function. As you probably know, with a NOT function and either an OR or an AND, you can build up XOR’s, adders, shift registers, and anything you need to perform computation.

We represent the output for various inputs as a truth table, where 0 = FALSE, and 1 = TRUE. You should verify that when W = 1 and theta = 1, we get the truth table for the logical NOT,

        Vin  |  Vout
        -----+------
          1  |   0
          0  |   1

by using this circuit:

With two excitatory inputs V₁ and V₂, and W =1, we can get either an OR or an AND, depending on the value of theta:

Can you verify that with these weights and thresholds, the various possible inputs for V₁ and V₂ result in this table?

        V1 | V2 | OR | AND
        ---+----+----+----
         0 |  0 |  0 |  0
         0 |  1 |  1 |  0
         1 |  0 |  1 |  0
         1 |  1 |  1 |  1

The exclusive OR (XOR) has the truth table:

        V1 | V2 | XOR
        ---+----+----
         0 |  0 |  0 
         0 |  1 |  1       (Note that this is also a
         1 |  0 |  1        "1 bit adder".)
         1 |  1 |  0

It cannot be represented with a single neuron, but the relationship
XOR = (V₁ OR V₂) AND NOT (V₁ AND V₂) suggests that it can be represented with the network

由於『XOR』邏輯函數並不能夠用『單一單層』之 MCP 神經元來『表現』的緣故！因此必得成為『網絡』的乎？就算這樣變成一個『通用計算機』的了，那麼它怎麼『學習』的呢？？經過了十五年之沉潛，而後 Frank Rosenblatt 提出了『感知器』模型︰

The Perceptron

The next major advance was the perceptron, introduced by Frank Rosenblatt in his 1958 paper. The perceptron had the following differences from the McCullough-Pitts neuron:

The weights and thresholds were not all identical.
Weights can be positive or negative.
There is no absolute inhibitory synapse.
Although the neurons were still two-state, the output function f(u) goes from [-1,1], not [0,1]. (This is no big deal, as a suitable change in the threshold lets you transform from one convention to the other.)
Most importantly, there was a learning rule.

Describing this in a slightly more modern and conventional notation (and with V_i = [0,1]) we could describe the perceptron like this:

This shows a perceptron unit, i, receiving various inputs I_j, weighted by a “synaptic weight” W_ij.

The ith perceptron receives its input from n input units, which do nothing but pass on the input from the outside world. The output of the perceptron is a step function:

and

A network of two perceptrons with three inputs would look like:

Specifically, and

where is the learning rate.

……

How many epochs does it take until the perceptron has been trained to generate the correct truth table for an OR? Note that, except for a scale factor, this is the same result which McCullogh and Pitts deduced for the weights and bias without letting the net do the learning. (Do you see why a positive threshold for a M-P neuron is equivalent to adding a negative bias term in the expression for the perceptron total input u?)

───

又將『人工神經網絡』推向新的高峰。只不過那個『XOR』的問題仍然麻煩︰

why do neurons make networks

On the logical operations page, I showed how single neurons can perform simple logical operations, but that they are unable to perform some more difficult ones like the XOR operation (shown above). and I described how an XOR network can be made, but didn’t go into much detail about why the XOR requires an extra layer for its solution. This page is about using the knowledge we have from the formalising & visualising page to help us understand why neurons need to make networks. The only network we will look at is the XOR, but at the end you will play with a network that visualises the XOR problem as a pair of lines through input space that you can adjust by changing the parameters of the neurons.

the xor problem

We have a problem that can be described with the logic table below, and visualised in input space as shown on the right.

……

況且到底該如何『教化』『神經網絡』『有效學習』的呢？？！！是因為『太簡略』，所以『理論』上根本不可能學會『太多』？？還是由於『很費時』，因此『實務』上很難有什麼價值！！

故到今日『思辨』依舊存在，無怪乎有人說︰

McCulloch-Pitts Neurons

Author: Michael Marsalli

Overview:

MODULE DESCRIPTION:

In 1943 Warren S. McCulloch, a neuroscientist, and Walter Pitts, a logician, published “A logical calculus of the ideas immanent in nervous activity” in the Bulletin of Mathematical Biophysics 5:115-133. In this paper McCulloch and Pitts tried to understand how the brain could produce highly complex patterns by using many basic cells that are connected together. These basic brain cells are called neurons, and McCulloch and Pitts gave a highly simplified model of a neuron in their paper. The McCulloch and Pitts model of a neuron, which we will call an MCP neuron for short, has made an important contribution to the development of artificial neural networks — which model key features of biological neurons.

The original MCP Neurons had limitations. Additional features were added which allowed them to “learn.” The next major development in neural networks was the concept of a perceptron which was introduced by Frank Rosenblatt in 1958. Essentially the perceptron is an MCP neuron where the inputs are first passed through some “preprocessors,” which are called association units. These association units detect the presence of certain specific features in the inputs. In fact, as the name suggests, a perceptron was intended to be a pattern recognition device, and the association units correspond to feature or pattern detectors.

……

也有人講︰

The McCulloch-Pitts Neuron

Written by Harry Fairhead

Article Index
The McCulloch-Pitts Neuron
What can the brain compute?

Page 1 of 2

Nowadays the McCulloch-Pitts neuron tends to be overlooked in favour of simpler neuronal models but they were and are still important. They proved that something that behaved like a biological neuron was capable of computation and early computer designers often thought in terms of them.

Before the neural network algorithms in use today were devised, there was an alternative. It was invented in 1943 by neurophysiologist Warren McCulloch and logician Walter Pitts. Now networks of the McCulloch-Pitts type tend to be overlooked in favour of “gradient descent” type neural networks and this is a shame. McCulloch-Pitts neurons are more like the sort of approach we see today in neuromorphic chips where neurons are used as computational units.

wsmcculloch

Warren McCulloch

pitts

Walter Pitts

What is interesting about the McCulloch-Pitts model of a neural network is that it can be used as the components of computer-like systems.

……

What can the brain compute?

You can see that it would be possible to continue in this way to build more and more complicated neural circuits using cells. Shift registers are easy, so are half and full adders – give them a try!

But at this point you might well be wondering why we are bothering at all?

The answer is that back in the early days of AI the McCulloch-Pitts neuron, and its associated mathematics, gave us clear proof that you could do computations with elements that looked like biological neurons.

To be more precise, it is relatively easy to show how to construct a network that will recognise or “accept” a regular expression. A regular expression is something that can be made up using simple rules. In terms of production rules any regular expression can be described by a grammar having rules of the type:

<non-terminal1> ->  symbol <non-terminal2>

<non-terminal1> -> symbol

That is, rules are only “triggered” in the right and symbols are only added at the left.

……

Why is this important?

Well if you agree that McCulloch-Pitts neurons capture the essence of the way biological neurons work then you also have to conclude that biological networks are just finite state machines and as such can only recognise or generate regular sequences.

In their original work McCulloch and Pitts extended this observation into deducing a great deal about human brain function. Most of this seems a bit far-fetched from today’s standpoint but the basic conclusion that the brain is probably nothing more than a simple computer – i.e. a finite state machine – still seems reasonable.

If you know a little about the theory of computation you might well not be happy about this “bottom line” because a finite state machine isn’t even as powerful as a Turing machine. That is, there are lots of things that a Turing machine can compute that in theory we, as finite state machines, can’t. In fact there are three or more complexities of grammar, and hence types of sequence, that finite state machines, and hence presumably us, cannot recognise.

This sort of argument is often used to demonstrate that there has to be more to a human brain than mere logic – it has a non-physical “mind” component or some strange quantum phenomena that are required to explain how we think.

All nonsense of course!

You shouldn’t get too worried about these conclusions because when you look at them in more detail some interesting facts emerge. For example, all finite sequences are regular and so we are really only worrying about philosophical difficulties that arise because we are willing to allow infinite sequences of symbols.

While this seems reasonable when the infinite sequence is just ABAB… it is less reasonable when there is no finite repetitive sequence which generates the chain. If you want to be philosophical about such things perhaps it would be better to distinguish between sequences that have no fixed length limit – i.e. unbounded but finite sequences – and truly infinite sequences.

Surprisingly, even in this case things work out in more or less the same way with finite state machines, and hence human brains, lagging behind other types of computer. The reason for this is simply that as soon as you consider a sequence longer than the number of elements in the brain it might as well be infinite!

As long as we restrict our attention to finite sequences with some upper limit on length, and assume that the number of computing elements available is much greater than this, then all computers are equal and the human brain is as good as anything!

McCulloch and Pitts neural networks are not well-known or widely studied these days because they grew into or were supersede by another sort of neural net – one that can be trained into generating any logic function or indeed any function you care to name.

───

樹莓派、樹莓派之學習、樹莓派之教育

W!o+ 的《小伶鼬工坊演義》︰神經網絡【Perceptron】一

2016-04-07 懸鉤子

閱讀 Michael Nielsen 所寫的『感知器』闡釋︰

Perceptrons

So how do perceptrons work? A perceptron takes several binary inputs, $x_1, x_2, \cdots$ $x_{1}, x_{2}, \dots$ , and produces a single binary output:

In the example shown the perceptron has three inputs, $x_1, x_2, x_3$

x_{1}, x_{2}, x_{3}

. In general it could have more or fewer inputs. Rosenblatt proposed a simple rule to compute the output. He introduced weights, $w_1,w_2,\cdots$

w_{1}, w_{2}, \dots

, real numbers expressing the importance of the respective inputs to the output. The neuron’s output,

0

1

, is determined by whether the weighted sum $\sum_j w_j x_j$

\sum_{j} w_{j} x_{j}

is less than or greater than some threshold value. Just like the weights, the threshold is a real number which is a parameter of the neuron. To put it in more precise algebraic terms:

output = \begin{cases}0 & \text{if } \sum_j w_j x_j \leq \ threshold\\1 & \text{if} \ \sum_j w_j x_j > \ threshold\end{cases}

That’s all there is to how a perceptron works!

……

當真單刀直入又簡潔直接！緊接說明如何用『感知器』建構邏輯閘『NAND』︰

I’ve described perceptrons as a method for weighing evidence to make decisions. Another way perceptrons can be used is to compute the elementary logical functions we usually think of as underlying computation, functions such as AND, OR, and NAND. For example, suppose we have a perceptron with two inputs, each with weight $- 2$ , and an overall bias of $3$ . Here’s our perceptron:

Then we see that input

00

produces output

1

, since $(-2)*0+(-2)*0+3 = 3$

(- 2) * 0 + (- 2) * 0 + 3 = 3

is positive. Here, I’ve introduced the

*

symbol to make the multiplications explicit. Similar calculations show that the inputs

01

and

10

produce output

1

. But the input

11

produces output

0

, since

(- 2) * 1 + (- 2) * 1 + 3 = - 1

is negative. And so our perceptron implements a NAND gate!

……

於是乎通熟邏輯者可以知道『感知器』的『網絡』能夠運算任何『邏輯表達式』！！

由於電流的『有無』和電壓的『高低』，與邏輯上的『真假』二態相似，所以很自然的布林代數也就進入『邏輯電路』的『設計』領域之中了。今天在『電子工程』領域裡的專業化了的布林代數叫做『邏輯代數』，而在『計算機科學』領域中之專門化的布林代數又稱作『布爾邏輯』。

一八八零年皮爾士已經發現『NAND』── Not AND ── 和『NOR』── Not OR ── 的邏輯『功能完備性』，還特別用了一個希臘語詞『ampheck』ἀμφήκης 雙刃，來表達它們都是『自足算子』；也就是說所有的邏輯表達式，都可以只用『NAND』或『NOR』構成。但是由於他從未發表過，於是三十三年後，一九一三年美國的 Henry M. Sheffer 於一篇提交給『Transactions of the American Mathematical Society 』的論文中，使用『豎線｜』Strock 表示 NAND，同時他也論證了這個公理系統的完備性；因此現今 NAND 被稱作『Sheffer豎線 』，而 NOR 也叫做『皮爾士箭頭』。不知又是誰先想到這給邏輯電路的『工程實作』帶來了巨大的『經濟性』和『簡易性』？？

未知何年何月，有一

孤虛者言︰
物有無者，非真假也。苟日新，日日新，又日新。真假者，物之論也。論也者，當或不當而已矣。故世有孤虛者，言有孤虛論。孤虛何謂也？甲乙孤虛，言不得全真也，索其孤其虛而已矣。天地孤虛，去其上下也，善惡孤虛，何得善惡並真乎？是故孤虛論全矣！其法曰︰物物孤虛，言物之非也；孤虛之孤虛，此孤虛之非也。使甲與乙並，此甲乙辜虛之非也，強使之或，乃非甲非乙之孤虛也。若云由此及彼，雖言之鑿鑿，若非彼與此之孤虛，无能以斷疑是也！！

─── 摘自《布林代數》

若是一個了解 λ 運算者，是否會將之描述成『感知器泛函』呢？

美國數學家阿隆佐‧邱奇 Alonzo Church 對『符號邏輯』symbolic logic 的熱情與對基礎算術『形式系統』的研究持續一生。當他發現這類系統容易受到『羅素悖論』影響時，轉將所設想的『λ 運算』lambda calculus 單獨用於研究『可計算性』問題，同樣否定的回答了『判定性問題』 Decision-problem ──

一九零零年德國大數學家大衛‧希爾伯特 David Hilbert 在巴黎的國際數學家大會上作了場名為《數學問題》的演講，提出了二十三道待解決之最重要的數學問題，這就是著名的希爾伯特之二十三個問題的由來。這裡的『判定性問題』就是二十三個問題的第二題『算術公理之相容性』，一九三零年已為庫爾特‧哥德爾所否證 ──。美國 UCLA 大學 Enderton, Herbert B. 教授寫了一篇名為
《INTRODUCTION
Alonzo Church: Life and Work》的 Alonzo Church 小傳︰
…
In 1936 a pair of papers by Church changed the course of logic. An Unsolvable Problem of Elementary Number Theory presents a definition and a theorem:
“The purpose of the present paper is to propose a definition of effective calculability which is thought to correspond satisfactorily to the somewhat vague intuitive notion . . . , and to show, by means of an example, that not every problem of this class is solvable.” The “definition” now goes by the name Church’s Thesis: “We now define the notion . . . of an effectively calculable function of positive integers by identifying it with the notion of a recursive function of positive integers (or of a λ-definable function of positive integers).” (The name, “Church’s Thesis,” was introduced by Kleene.)
The theorem in the paper is that there is a set that can be defined in the language of elementary number theory (viz. the set of G ̈odel numbers of formulas of the λ-calculus having a normal form) that is not recursive—although it is recursively enumerable. Thus truth in elementary number theory is an effectively unsolvable problem.

A sentence at the end of the paper adds the consequence that if the system of Principia Mathematica is ω-consistent, then its decision problem is unsolvable. It also follows that the system (if ω-consistent) is incomplete, but of course G ̈odel had shown that in 1931.
…

λ演算是一套用來研究『函式』Function 的『抽象』Abstraction 、函式的『應用』Apply 、『變元』Variable 的『替換』Substitution 以及『函式』之『化約』reduction 的形式語言。λ演算對於泛函式程式語言的興起有著巨大的推動力，比方說人工智慧領域著名的 Lisp 語言，以及後來的 ML 語言和 Haskell 語言。更令人驚訝的是它自身就是一個『世界上最小的通用性程式語言』。由於『函式』與『變元』兩者是任何人不管想用哪種『□□程式語言』來寫『演算法』Algorithm 都需要清楚理解的概念。就讓我們踏上前人走過的足跡，回顧旅途上周遭景緻，說不定會有意外的收穫！！

─── 摘自《λ 運算︰淵源介紹》

終究『感知器』之『網絡』也不過是另一種『計算機』而已？？

The computational universality of perceptrons is simultaneously reassuring and disappointing. It’s reassuring because it tells us that networks of perceptrons can be as powerful as any other computing device. But it’s also disappointing, because it makes it seem as though perceptrons are merely a new type of NAND gate. That’s hardly big news!

However, the situation is better than this view suggests. It turns out that we can devise learning algorithms which can automatically tune the weights and biases of a network of artificial neurons. This tuning happens in response to external stimuli, without direct intervention by a programmer. These learning algorithms enable us to use artificial neurons in a way which is radically different to conventional logic gates. Instead of explicitly laying out a circuit of NAND and other gates, our neural networks can simply learn to solve problems, sometimes problems where it would be extremely difficult to directly design a conventional circuit.

───

當然是！但它『自動改寫』！！

最後我們介紹一下『何謂 Thue 之改寫系統』？結束這個《系列》的第一篇。阿克塞爾‧圖厄【挪威語 Axel Thue】一位數學家，以研究丟番圖用『有理數』逼近『實數』問題以及開拓『組合數學』之貢獻而聞名。他於一九一四發表了『詞之群論問題』Word problem for group 啟始了一個今天稱之為『字串改寫系統』SRS String Rewriting System 的先河，如從現今的研究和發現來看，它與圖靈機的『停機問題』密切相關。上個千禧年之時，John Colagioia 用『Semi-Thue System』寫了一個『奧秘的』 esoteric 程式語言 Thue ，作者宣稱︰

Thue represents one of the simplest possible ways to construe 『constraint-based』基於約束 programming. It is to the constraint-based 『paradigm』典範 what languages like『 OISC 』── 單指令集電腦 One instruction set computer ── are to the imperative paradigm; in other words, it’s a 『tar pit』焦油坑.

─── 摘自《 Thue 之改寫系統《一》》

彷彿本源自仙女之『圖靈機』也！！？？

看來仙女早已遠離，那就說說存在的這台『圖靈機』吧！根據『 Hopcroft, John E.; Ullman, Jeffrey D. (1979). Introduction to Automata Theory, Languages, and Computation (1st ed.)』所定義︰

『單磁帶』one-tape 圖靈機是一個有序七元組 $M= \langle Q, \Gamma, b, \Sigma, \delta, q_0, F \rangle$ ，此處

$Q$ 是一個有限非空的『狀態』 state 集合

$\Gamma$ 是一個有限非空的『磁帶上字母符號』集合

$b \in \Gamma$ 是一個『空白符號』，唯一允許在任意計算步驟中無限次出現在磁帶上的符號

$\Sigma\subseteq\Gamma\setminus\{b\}$ 是不包含空白符號的『輸入符號』集合

$q_0 \in Q$ 是『初始狀態』

$F \subseteq Q$ 是『最終狀態』或稱作『接受狀態』，一般可能有 $q_{accept}, q_{reject},q_{HALT}$

$\delta: Q \setminus F \times \Gamma \rightarrow Q \times \Gamma \times \{L,R\}$ 是稱作『轉移函式』transition function，其中 $L,R$ 代表『讀寫頭』之向『左，右』移動，還有的增加了『不移動』no shift 的擴張

圖靈機 $M$ 將以下面方式運行：

開機的時候首先將輸入符號字串 $\omega=\omega_0\omega_1\ldots\omega_{n-1} \in \Sigma^*$ 依序的從左到右填寫在磁帶之第 $0, 1, \ldots , n-1$ 編號的格子上，將所有其它格子保持空白 ── 即填以空白符 $b$ ──。然後 $M$ 的讀寫頭指向第 $0$ 號格子，此時 $M$ 處於狀態 $q_0$ 。機器開始執行指令，按照轉移函式 $\delta$ 所描述的規則進行逐步計算。比方如果當前機器的狀態是 $q$ ，讀寫頭所指的格子中的符號是 $x$ ，假使 $\delta(q,x) = (q', x', L)$ ，那麼機器下一步將進入新的狀態 $q'$ ，且將讀寫頭所指的格子中的符號改寫為 $x'$ ，然後把讀寫頭向左移動一個格子。設使在某一時刻，讀寫頭所指的是第 $0$ 號格子，然而根據轉移函式它的下一步又將繼續向左移，此時它停在原處不動，也就是說，讀寫頭永遠不會移出了磁帶的左方界限。設若在某個時刻 $M$ 根據轉移函式進入了某種最終狀態 $q_{final}$ ，則它立刻停機並留下磁帶上的結果字串。由於轉移函式 $\delta$ 是一個部分函式，換句話說對於某些 $q,x, \ \delta(q,x)$ 可能沒有可用的轉移定義，如果在執行中遇到這種情況，機器依設計約定也將立即 $q_{HALT}$ 停機。

─── 摘自《紙張、鉛筆和橡皮擦》

所以才瞎子摸象說法林立的耶？？！！

樹莓派、樹莓派之學習、樹莓派之教育

W!o+ 的《小伶鼬工坊演義》︰神經網絡與深度學習【發凡】

2016-04-06 懸鉤子

對一本小巧完整而且寫的好的書，又該多說些什麼的呢？於是幾經思慮，就講講過去之閱讀隨筆與念頭雜記的吧！終究面對一個既舊也新的議題，尚待火石電光激發創意和發想。也許只需一個洞見或將改變人工智慧的未來乎？？

Michael Nielsen 先生開宗明義在首章起頭

The human visual system is one of the wonders of the world. Consider the following sequence of handwritten digits:

Most people effortlessly recognize those digits as 504192. That ease is deceptive. In each hemisphere of our brain, humans have a primary visual cortex, also known as V1, containing 140 million neurons, with tens of billions of connections between them. And yet human vision involves not just V1, but an entire series of visual cortices – V2, V3, V4, and V5 – doing progressively more complex image processing. We carry in our heads a supercomputer, tuned by evolution over hundreds of millions of years, and superbly adapted to understand the visual world. Recognizing handwritten digits isn’t easy. Rather, we humans are stupendously, astoundingly good at making sense of what our eyes show us. But nearly all that work is done unconsciously . And so we don’t usually appreciate how tough a problem our visual systems solve.

The difficulty of visual pattern recognition becomes apparent if you attempt to write a computer program to recognize digits like those above. What seems easy when we do it ourselves suddenly becomes extremely difficult. Simple intuitions about how we recognize shapes – “a 9 has a loop at the top, and a vertical stroke in the bottom right” – turn out to be not so simple to express algorithmically. When you try to make such rules precise, you quickly get lost in a morass of exceptions and caveats and special cases. It seems hopeless.

Neural networks approach the problem in a different way. The idea is to take a large number of handwritten digits, known as training examples,

and then develop a system which can learn from those training examples. In other words, the neural network uses the examples to automatically infer rules for recognizing handwritten digits. Furthermore, by increasing the number of training examples, the network can learn more about handwriting, and so improve its accuracy. So while I’ve shown just 100 training digits above, perhaps we could build a better handwriting recognizer by using thousands or even millions or billions of training examples.

In this chapter we’ll write a computer program implementing a neural network that learns to recognize handwritten digits. The program is just 74 lines long, and uses no special neural network libraries. But this short program can recognize digits with an accuracy over 96 percent, without human intervention. Furthermore, in later chapters we’ll develop ideas which can improve accuracy to over 99 percent. In fact, the best commercial neural networks are now so good that they are used by banks to process cheques, and by post offices to recognize addresses.

We’re focusing on handwriting recognition because it’s an excellent prototype problem for learning about neural networks in general. As a prototype it hits a sweet spot: it’s challenging – it’s no small feat to recognize handwritten digits – but it’s not so difficult as to require an extremely complicated solution, or tremendous computational power. Furthermore, it’s a great way to develop more advanced techniques, such as deep learning. And so throughout the book we’ll return repeatedly to the problem of handwriting recognition. Later in the book, we’ll discuss how these ideas may be applied to other problems in computer vision, and also in speech, natural language processing, and other domains.

Of course, if the point of the chapter was only to write a computer program to recognize handwritten digits, then the chapter would be much shorter! But along the way we’ll develop many key ideas about neural networks, including two important types of artificial neuron (the perceptron and the sigmoid neuron), and the standard learning algorithm for neural networks, known as stochastic gradient descent. Throughout, I focus on explaining why things are done the way they are, and on building your neural networks intuition. That requires a lengthier discussion than if I just presented the basic mechanics of what’s going on, but it’s worth it for the deeper understanding you’ll attain. Amongst the payoffs, by the end of the chapter we’ll be in position to understand what deep learning is, and why it matters.

………

說明這本書的主旨。是用『手寫阿拉伯數字辨識』這一主題貫串『神經網絡』以及『深度學習』之點滴，希望讀者能夠藉著最少的文本一窺全豹、聞一知十。因此他盡量少用『數學』，盡可能白話描述重要的『原理』與『概念』。通常不以『機器學習』

機器學習是近20多年興起的一門多領域交叉學科，涉及機率論、統計學、逼近論、凸分析、計算複雜性理論等多門學科。機器學習理論主要是設計和分析一些讓計算機可以自動「學習」的算法。機器學習算法是一類從數據中自動分析獲得規律，並利用規律對未知數據進行預測的算法。因為學習算法中涉及了大量的統計學理論，機器學習與推斷統計學聯繫尤為密切，也被稱為統計學習理論。算法設計方面，機器學習理論關注可以實現的，行之有效的學習算法。很多推論問題屬於無程序可循難度，所以部分的機器學習研究是開發容易處理的近似算法。

機器學習已廣泛應用於數據挖掘、計算機視覺、自然語言處理、生物特徵識別、搜尋引擎、醫學診斷、檢測信用卡欺詐、證券市場分析、DNA序列測序、語音和手寫識別、戰略遊戲和機器人等領域。

定義

機器學習有下面幾種定義：

機器學習是一門人工智慧的科學，該領域的主要研究對象是人工智慧，特別是如何在經驗學習中改善具體算法的性能。
機器學習是對能通過經驗自動改進的計算機算法的研究。
機器學習是用數據或以往的經驗，以此優化電腦程式的性能標準。

一種經常引用的英文定義是：A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.

分類

機器學習可以分成下面幾種類別：

監督學習從給定的訓練數據集中學習出一個函數，當新的數據到來時，可以根據這個函數預測結果。監督學習的訓練集要求是包括輸入和輸出，也可以說是特徵和目標。訓練集中的目標是由人標註的。常見的監督學習算法包括回歸分析和統計分類。
無監督學習與監督學習相比，訓練集沒有人為標註的結果。常見的無監督學習算法有聚類。
半監督學習介於監督學習與無監督學習之間。
增強學習通過觀察來學習做成如何的動作。每個動作都會對環境有所影響，學習對象根據觀察到的周圍環境的反饋來做出判斷。

───

種種術語打攪讀者。固然這對初次接觸者有很大的好處，然而這對『人工智慧』之叢林而言恐怕稍嫌不足。就像那個帶註解的程式

network.py

tikz12

"""
network.py
~~~~~~~~~~

A module to implement the stochastic gradient descent learning
algorithm for a feedforward neural network.  Gradients are calculated
using backpropagation.  Note that I have focused on making the code
simple, easily readable, and easily modifiable.  It is not optimized,
and omits many desirable features.
"""

#### Libraries
# Standard library
import random

# Third-party libraries
import numpy as np

class Network(object):

    def __init__(self, sizes):
        """The list ``sizes`` contains the number of neurons in the
        respective layers of the network.  For example, if the list
        was [2, 3, 1] then it would be a three-layer network, with the
        first layer containing 2 neurons, the second layer 3 neurons,
        and the third layer 1 neuron.  The biases and weights for the
        network are initialized randomly, using a Gaussian
        distribution with mean 0, and variance 1.  Note that the first
        layer is assumed to be an input layer, and by convention we
        won't set any biases for those neurons, since biases are only
        ever used in computing the outputs from later layers."""
        self.num_layers = len(sizes)
        self.sizes = sizes
        self.biases = [np.random.randn(y, 1) for y in sizes[1:]]
        self.weights = [np.random.randn(y, x)
                        for x, y in zip(sizes[:-1], sizes[1:])]

    def feedforward(self, a):
        """Return the output of the network if ``a`` is input."""
        for b, w in zip(self.biases, self.weights):
            a = sigmoid(np.dot(w, a)+b)
        return a

    def SGD(self, training_data, epochs, mini_batch_size, eta,
            test_data=None):
        """Train the neural network using mini-batch stochastic
        gradient descent.  The ``training_data`` is a list of tuples
        ``(x, y)`` representing the training inputs and the desired
        outputs.  The other non-optional parameters are
        self-explanatory.  If ``test_data`` is provided then the
        network will be evaluated against the test data after each
        epoch, and partial progress printed out.  This is useful for
        tracking progress, but slows things down substantially."""
        if test_data: n_test = len(test_data)
        n = len(training_data)
        for j in xrange(epochs):
            random.shuffle(training_data)
            mini_batches = [
                training_data[k:k+mini_batch_size]
                for k in xrange(0, n, mini_batch_size)]
            for mini_batch in mini_batches:
                self.update_mini_batch(mini_batch, eta)
            if test_data:
                print "Epoch {0}: {1} / {2}".format(
                    j, self.evaluate(test_data), n_test)
            else:
                print "Epoch {0} complete".format(j)

    def update_mini_batch(self, mini_batch, eta):
        """Update the network's weights and biases by applying
        gradient descent using backpropagation to a single mini batch.
        The ``mini_batch`` is a list of tuples ``(x, y)``, and ``eta``
        is the learning rate."""
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        for x, y in mini_batch:
            delta_nabla_b, delta_nabla_w = self.backprop(x, y)
            nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
            nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
        self.weights = [w-(eta/len(mini_batch))*nw
                        for w, nw in zip(self.weights, nabla_w)]
        self.biases = [b-(eta/len(mini_batch))*nb
                       for b, nb in zip(self.biases, nabla_b)]

    def backprop(self, x, y):
        """Return a tuple ``(nabla_b, nabla_w)`` representing the
        gradient for the cost function C_x.  ``nabla_b`` and
        ``nabla_w`` are layer-by-layer lists of numpy arrays, similar
        to ``self.biases`` and ``self.weights``."""
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        # feedforward
        activation = x
        activations = [x] # list to store all the activations, layer by layer
        zs = [] # list to store all the z vectors, layer by layer
        for b, w in zip(self.biases, self.weights):
            z = np.dot(w, activation)+b
            zs.append(z)
            activation = sigmoid(z)
            activations.append(activation)
        # backward pass
        delta = self.cost_derivative(activations[-1], y) * \
            sigmoid_prime(zs[-1])
        nabla_b[-1] = delta
        nabla_w[-1] = np.dot(delta, activations[-2].transpose())
        # Note that the variable l in the loop below is used a little
        # differently to the notation in Chapter 2 of the book.  Here,
        # l = 1 means the last layer of neurons, l = 2 is the
        # second-last layer, and so on.  It's a renumbering of the
        # scheme in the book, used here to take advantage of the fact
        # that Python can use negative indices in lists.
        for l in xrange(2, self.num_layers):
            z = zs[-l]
            sp = sigmoid_prime(z)
            delta = np.dot(self.weights[-l+1].transpose(), delta) * sp
            nabla_b[-l] = delta
            nabla_w[-l] = np.dot(delta, activations[-l-1].transpose())
        return (nabla_b, nabla_w)

    def evaluate(self, test_data):
        """Return the number of test inputs for which the neural
        network outputs the correct result. Note that the neural
        network's output is assumed to be the index of whichever
        neuron in the final layer has the highest activation."""
        test_results = [(np.argmax(self.feedforward(x)), y)
                        for (x, y) in test_data]
        return sum(int(x == y) for (x, y) in test_results)

    def cost_derivative(self, output_activations, y):
        """Return the vector of partial derivatives \partial C_x /
        \partial a for the output activations."""
        return (output_activations-y)

#### Miscellaneous functions
def sigmoid(z):
    """The sigmoid function."""
    return 1.0/(1.0+np.exp(-z))

def sigmoid_prime(z):
    """Derivative of the sigmoid function."""
    return sigmoid(z)*(1-sigmoid(z))

是屬於

監督式學習

監督式學習（英語：Supervised learning），是一個機器學習中的方法，可以由訓練資料中學到或建立一個模式（函數 / learning model），並依此模式推測新的實例。訓練資料是由輸入物件（通常是向量）和預期輸出所組成。函數的輸出可以是一個連續的值（稱為迴歸分析），或是預測一個分類標籤（稱作分類）。

一個監督式學習者的任務在觀察完一些訓練範例（輸入和預期輸出）後，去預測這個函數對任何可能出現的輸入的值的輸出。要達到此目的，學習者必須以”合理”（見歸納偏向）的方式從現有的資料中一般化到非觀察到的情況。在人類和動物感知中，則通常被稱為概念學習（concept learning）。

回顧

監督式學習有兩種形態的模型。最一般的，監督式學習產生一個全域模型，會將輸入物件對應到預期輸出。而另一種，則是將這種對應實作在一個區域模型。（如案例推論及最近鄰居法）。為了解決一個給定的監督式學習的問題（手寫辨識），必須考慮以下步驟：

決定訓練資料的範例的形態。在做其它事前，工程師應決定要使用哪種資料為範例。譬如，可能是一個手寫字符，或一整個手寫的辭彙，或一行手寫文字。
搜集訓練資料。這資料須要具有真實世界的特徵。所以，可以由人類專家或（機器或感測器的）測量中得到輸入物件和其相對應輸出。
決定學習函數的輸入特徵的表示法。學習函數的準確度與輸入的物件如何表示是有很大的關聯度。傳統上，輸入的物件會被轉成一個特徵向量，包含了許多關於描述物件的特徵。因為維數災難的關係，特徵的個數不宜太多，但也要足夠大，才能準確的預測輸出。
決定要學習的函數和其對應的學習演算法所使用的資料結構。譬如，工程師可能選擇人工神經網路和決策樹。
完成設計。工程師接著在搜集到的資料上跑學習演算法。可以藉由將資料跑在資料的子集（稱為驗證集）或交叉驗證（cross-validation）上來調整學習演算法的參數。參數調整後，演算法可以運行在不同於訓練集的測試集上

另外對於監督式學習所使用的辭彙則是分類。現著有著各式的分類器，各自都有強項或弱項。分類器的表現很大程度上地跟要被分類的資料特性有關。並沒有某一單一分類器可以在所有給定的問題上都表現最好，這被稱為『天下沒有白吃的午餐理論』。各式的經驗法則被用來比較分類器的表現及尋找會決定分類器表現的資料特性。決定適合某一問題的分類器仍舊是一項藝術，而非科學。

目前最廣泛被使用的分類器有人工神經網路、支持向量機、最近鄰居法、高斯混合模型、樸素貝葉斯方法、決策樹和徑向基函數分類。

這一類範疇，事實上那裡曾經提出過多種『機器學習』之方法！！誰知道未來誰奪魁的耶？？

FreeSandal

每月彙整: 2016 年 4 月

W!o+ 的《小伶鼬工坊演義》︰神經網絡【Perceptron】四

Hebbian theory

Principles

Generalization and stability

The Perceptron

W!o+ 的《小伶鼬工坊演義》︰神經網絡【Perceptron】三

感知器

歷史

Perceptrons

W!o+ 的《小伶鼬工坊演義》︰神經網絡【Perceptron】二

神經元

Some specific models of artificial neural nets

McCullogh-Pitts Model

The Perceptron

why do neurons make networks

the xor problem

What can the brain compute?

W!o+ 的《小伶鼬工坊演義》︰神經網絡【Perceptron】一

Perceptrons

W!o+ 的《小伶鼬工坊演義》︰神經網絡與深度學習【發凡】

CHAPTER 1

Using neural nets to recognize handwritten digits

定義

分類

監督式學習

回顧

輕。鬆。學。部落客

2016 年 4 月
日	一	二	三	四	五	六
« 3 月				5 月 »
					1	2
3	4	5	6	7	8	9
10	11	12	13	14	15	16
17	18	19	20	21	22	23
24	25	26	27	28	29	30